Полный факторный эксперимент

Метод полного факторногоэксперимента дает возможность получить математическое описание исследуемого процесса в некоторой локальнойобласти факторного пространства, лежащей в окрестности выбранной точки скоординатами (x₀₁, х₀₂,…, x_0n) [1, 2].

Итак, с помощью полного факторного эксперимента ищут математическое описание процесса в виде уравнения:

y=b₀+b₁x₁+b₂x₂+…b_nx_n+b₁₂x₁₂+ b_(n-1)nx_(n-1)x_n (3.1)

Его называют уравнением регрессии, а входящие в него коэффициенты - коэффициентами регрессии.

Для удобства вычислений коэффициентов регрессии все факторы в ходе полного факторного эксперимента варьируют на двух уровнях, соответствующих значениям кодированных переменных -1 и +1.

Таким образом, полным факторным экспериментом называется система опытов, содержащая все возможные неповторяющиеся комбинации уровней варьирования факторов.

В табл. 3.1 приведены условия опытов полного двухфакторного эксперимента. Часть таблицы, обведенная пунктиром, называется матрицей планирования.

Таблица 3.1 - Полный двухфакторный эксперимент

Номер опыта	Факторы	Функция отклика
	-1	y1
	+1	y2
	-1	y3
	+1	y4

В табл. 3.2 приведены условия опытов полного трехфакторного эксперимента. Эти опыты соответствуют в факторном пространстве вершинам куба с центром в начале координат.

Таблица 3.2 - Полный трехфакторный эксперимент

Номер опыта	Факторы	Функция отклика
x1	x1	x1
	-1	-1	-1	y1
	+1	-1	-1	y2
	-1	+1	-1	y3
	+1	+1	-1	y4
	-1	-1	+1	y5
	+1	-1	+1	y6
	-1	+1	+1	y7
	+1	+1	+1	y8

Из табл. 3.1 и 3.2 видны основные принципы построения матриц планирования полного факторного эксперимента;

- уровни варьирования первого фактора чередуются от опыта к опыту;

- частота смены уровней варьирования каждого последующего фактора вдвое меньше, чем у предыдущего.

Матрица планирования полного факторного эксперимента является ортогональной. Это свойство позволяет вычислять коэффициенты регрессии по простым формулам независимо друг от друга [27].

Общее количество опытов в матрице планирования:

N=2ⁿ, (3.2)

где п — число факторов.

На основании полного факторного эксперимента вычисляют коэффициенты регрессии, пользуясь следующими формулами:

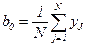; (3.3)

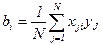; (3.4)

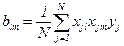, (3.5)

где l≠m.

Некоторые из коэффициентов регрессии могут оказаться пренебрежимо малыми - незначимыми. Чтобы установить, значим коэффициент или нет, необходимо, прежде всего, вычислить оценку дисперсии, с которой он определяется:

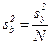(3.6)

Следует отметить, что с помощью полного факторного эксперимента все коэффициенты определяются с одинаковойпогрешностью.

Принято считать, что коэффициент регрессии значим, если выполнено условие:

b>s_bt (3.7)

где t — значение критерия Стьюдента.

В противном случае коэффициент регрессии незначим, и соответствующий член можно исключить из уравнения.

Получив уравнение регрессии, следует проверить его адекватность, т. е. способность достаточно хорошо описывать поверхность отклика. Эту проверку осуществляют с помощью критерия Фишера, который представляет собой следующее отношение:

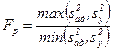, (3.8)

где s_ад — оценка дисперсии адекватности.

В числителе дроби (3.8) находится большая, а в знаменателе - меньшая из указанных оценок дисперсий.

Оценку дисперсии адекватности вычисляют по формуле

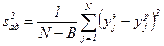, (3.9)

где В - число коэффициентов регрессии искомого уравнения, включая и свободный член; у_j^э, y_j ^р- экспериментальное и расчетное значение функции отклика в j-м опыте; N - число опытов полного факторного эксперимента.

С оценкой дисперсии адекватности связано число степеней свободы:

f_ад=N-B. (3.10)

Уравнение регрессии считается адекватным, если выполняется условие:

F_P≤F, (3.11)

где F —значение критерия Фишера.