Представление кратчайших путей в алгоритме

Часто требуется не просто подсчитать веса кратчайших путей, но и найти сами эти пути. Пусть G = (V, E) - заданный граф. Для каждой вершины 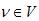будем помнить её предшественника 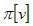. Предшественик вершины - это либо другая вершина, либо NIL. По завершении работы алгоритмов цепочка предшественников, начинающаяся с произвольной вершины v, будет представлять собой кратчайший путь из s в v, так что, если 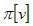≠ NIL, процедура Print-Path (G,s,v) напечатает кратчайший путь из s в v.

До завершения работы алгоритмов цепочки, получаемые итерациями π, не обязательно будут кратчайшими путями, но всё равно можно рассмотреть ориентированный подграф предшествования G_π = (V_π, E_π), определенный так: вершины G_π - это те вершины G, у которых предшественник отличен от NIL, плюс исходная вершина:

V_π = {v 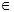V: π [ v ] ≠ NIL} 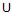{ s }

. Рёбра G _π - это стрелки, указывающие из π [ v ] ≠ NIL в v:

E_π = {(π [ v 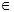], v) E: v 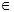V_π \ {s}}

Дерево кратчайших путей с корнем в s есть ориентированный подграф G´ = (V´, E´),

где V ´ 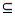V и E ´ 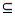E, для которого:

V ´ - множество вершин, достижимых из вершины s,
G ´ является деревом с корнем s,
для каждого v 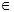V ´ путь из s в v в графе G ´ является кратчайшим путем из s в v в графе G.