Общеметодические подходы к количественной оценке риска

ГЛАВА 4 СИСТЕМА КОЛИЧЕСТВЕННЫХ ОЦЕНОК

ЭКОНОМИЧЕСКОГО РИСКА

Общеметодические подходы к количественной оценке риска

Риск - категория вероятностная, поэтому в процессе оценки неопределенности и количественного определения степени риска используют вероятностные расчеты.

Как отмечалось ранее, одним из наиболее распространенных методов количественной оценки риска является статистический метод.

Главными инструментами статистического метода расчета риска являются:

- среднее значение (m) изучаемой случайной величины (последствий какого-либо действия, например, дохода, прибыли и т.п.);

- дисперсия (s ² );

- стандартное (среднеквадратическое) отклонение (s);

- коэффициент вариации (V);

- распределение вероятности изучаемой случайной величины.

Из теории статистики известно, что для ограниченного числа (n) возможных значений случайной величины ее среднее значение определяется из выражения

_n

m = å X _i P_i,

ⁱ⁼¹

где Х_і - значение случайной величины;

Р_і - вероятность появления случайной величины.

Средняя величина представляет собой обобщенную количественную характеристику ожидаемого результата.

Важной характеристикой, определяющей меру изменчивости возможного результата является дисперсия - средневзвешенное из квадратов отклонений действительных результатов от средних,

_n

s² = å (Х_і - m)² P_i ,

ⁱ⁼¹

а также очень близко с ним связанное среднеквадратическое отклонение, определяемое из выражения

_n

s = Ö s² = Ö å (Х_і - m)² P_i ,

ⁱ⁼¹

Дисперсия и среднеквадратическое отклонение служат мерами абсолютного рассеянияи измеряются в тех же физических единицах, в каких измеряется варьирующий признак.

Для анализа меры изменчивости часто используют коэффициент вариации, который представляет собой отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений

V = s/m

Коэффициент вариации - относительная величина. Поэтому с его помощью можно сравнивать колеблемость признаков выраженных в различных единицах измерений.

Поскольку на формирование ожидаемого результата (например, величины прибыли) воздействует множество случайных факторов, то он естественно является случайной величиной

Одной из характеристик случайной величины Х является закон распределения ее вероятностей.

Характер, тип распределения отражает общие условия, вытекающие из сущности и природы явления, и особенности, оказывающие влияние на вариацию исследуемого показателя (ожидаемого результата).

Как показывает практика, для характеристики распределения социально-экономических явлений наиболее часто используется, так называемое, нормальное распределение.

Допущение о том, что большинство результатов хозяйственной деятельности (доходы, прибыль и т.п.), как случайные величины подчиняются закону, близкому к нормальному широко используется в литературе по проблеме количественной оценки экономического риска [28,51,54].

Известно, что закон нормального распределения характерен для распределения событий в случае, когда их исход представляет собой результат совместного воздействия большого количества независимых факторов и ни один из этих факторов не оказывает преобладающего влияния.

В действительности нормальное распределение экономических явлений в чистом виде встречается редко, однако, если однородность совокупности соблюдена, часто фактические распределения близки к нормальному.

На практике для проверки обоснованности принятого распределения используются различные критерии согласия (между эмпирическим и теоретическим распределением), которые позволяют принять или отвергнуть принятую гипотезу о законе распределения.

Из курса теории вероятностей и математической статистики известно, что нормально распределенная случайная величина является непрерывной и ее дифференциальная функция распределения имеет вид:

- (x -`m)²

1 2s²

y = f (x) = e,

s Ö 2p

где, у = f (Х) - определяет плотность распределения вероятности для каждой точки Х.

График функции нормального распределения описывается, так называемой, нормальной кривой (кривой Гаусса) - рис. 4.1.

Важным свойством графика дифференциальной функции нормального распределения является то, что площадь ограниченная нормальной кривой и осью Х всегда равна единице.

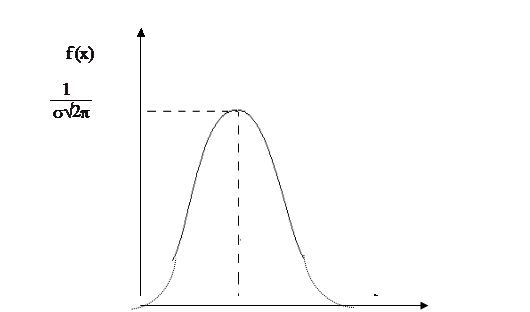
Рис. 3.1

m х

Рис.4.1 График функции нормального распределения

Использование функции плотности нормального распределения позволяет вычислить частоту (вероятность) появления случайной величины.

Для оценки вероятности попадания случайной величины в определенный интервал используют интегральную функцию плотности вероятности Ф (Х).

х

Ф (Х) =

-¥

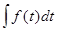
Вероятность попадания случайной величины в интервал (a,b) определится следующим образом

b

Р (a< C < b) = Ф (b) - Ф(a) = ,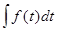

a

где f (t) - дифференциальная функция нормального распределения.

Изложенные выше положения являются исходной базой, применяемой для количественной оценки риска с использованием статистических методов.

Полагаем в дальнейшем, что исследуемая величина имеет (подчиняется) нормальный закон распределения.

Зададим максимально допустимое отклонение ожидаемого результата, которое составит определенную величину D.

Тогда границы, в которых должен находиться этот результат составят Х*=Х_ож - D; Х** = Х_ож + D.. Это положение отображено на рис.4.2

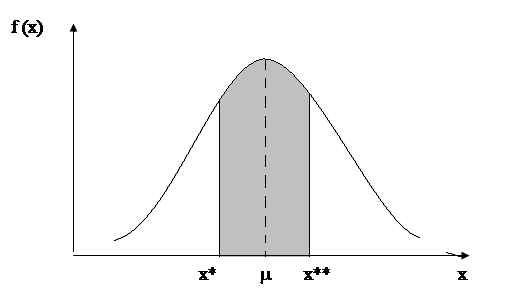
Рис.4.2

В общем случае нет необходимости предполагать соответствие Х_ож и m, и следовательно ожидаемая (планируемая, желаемая) величина может отличаться от средней. На рис.4.2 конструкция величин X* и X** фиксирует симметричное распределение. В общем случае при D₁ ¹ D₂ границы возможных изменений по отношению к ожидаемой (запланированной) величине располагаются асимметрично (рис.4.З).

Исходя из смысла функции плотности распределения, вероятность того, что достигаемый результат будет находиться в допустимых пределах (P₁) определится из выражения

_х**

P₁ = Р (X* £ Х_ож £ X**) = ò f (X) dx,

^х*

где f(x) - функция плотности распределения изучаемой (рассматриваемой) величины.

f (x)

х* m х_ож х** х

Рис. 4.3

Желаемый результат вероятности может быть получен подсчетом площади заштрихованного участка на рис. 4.2 и рис.4.3

Полученную таким образом вероятность P₁ мы будем называть уровнем вероятности достижения ожидаемого (планируемого) результата.

Естественно сразу же возникает вопрос о том какова вероятность попадания величины Х_ож за пределы допустимых границ (Р₂). Вычислив площадь не заштрихованного участка на рис. 4.2 и рис.4.3 мы получаем ответ на этот вопрос.

Исходя из характеристики (свойств) кривой нормального распределения, можно утверждать, что событие, состоящее в том, что случайная величина примет значение на интервале оси X, ограниченном нормальной кривой является достоверным, т.е. его вероятность равна 1.

Тогда

Р₂ = Р(Х_ож < X*) + Р (Х_ож > Х**) =1- P(X* £ Х_ож £. X**)

т.е. P₂ = 1 - P₁

Вероятность Р₂ оценивает неопределенность результата.

Как правило, граница в положительную сторону (направление) изменения ожидаемого результата не устанавливается, поэтому при определении Р ₂ , в большинстве случаев, речь идет только о величине Р ₂ = Р (Х _ож < Х*).

Таким образом, на практике фигура площади всегда является несимметричной.

Следует отметить, что отдельные авторы считают непосредственным измерителем риска величину Р₂.

Действительно, в относительно простых случаях для оценки степени риска можно использовать величину вероятности получения отрицательного результата (Р₂).

Однако, как следует из рассмотренного выше определения риска, существенные факторы понятия риска, здесь даже не затрагиваются. Поскольку наши повседневные оценки риска всегда базируются на сравнении возможных выигрышных исходов и обстоятельств, способствующих им, с возможными потерями в случае неудачи.

Поэтому вернемся к рассуждениям о возможности численного выражения риска с учетом оценки выигрыша и возможных потерь.