Тригонометрическим рядом Фурье функции 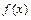 на отрезке
на отрезке 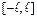 называется функциональный ряд вида
называется функциональный ряд вида 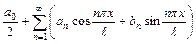 , где числа
, где числа 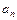 и
и 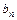 , называемые коэффициентами Фурье функции
, называемые коэффициентами Фурье функции 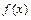 , вычисляются по формулам:
, вычисляются по формулам:
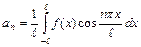 ,
, 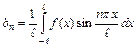 ,
, 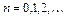 .
.
Функция 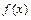 называется кусочно-монотонной на отрезке
называется кусочно-монотонной на отрезке 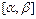 , если этот отрезок можно разбить конечным числом точек
, если этот отрезок можно разбить конечным числом точек 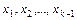 на интервалы
на интервалы 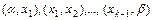 так, что на каждом из интервалов функция либо только возрастает, либо только убывает, либо постоянна.
так, что на каждом из интервалов функция либо только возрастает, либо только убывает, либо постоянна.
Если функция 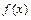 на отрезке
на отрезке 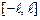 кусочно-монотонна и непрерывна, за исключением, быть может, конечного числа точек разрыва первого рода, то во всякой точке
кусочно-монотонна и непрерывна, за исключением, быть может, конечного числа точек разрыва первого рода, то во всякой точке 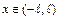 , в которой
, в которой 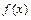 непрерывна, функцию можно разложить в тригонометрический ряд Фурье
непрерывна, функцию можно разложить в тригонометрический ряд Фурье 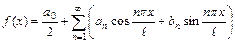 . В точках разрыва
. В точках разрыва 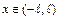 функции
функции 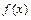 и точках
и точках 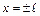 сумма ряда Фурье определяется формулами
сумма ряда Фурье определяется формулами 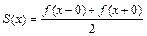 и
и 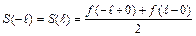 .
.
В частности, если: 1) функция 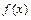 - чётная, то в точках
- чётная, то в точках 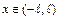 непрерывности функции имеет место разложение
непрерывности функции имеет место разложение 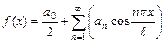 ,где
,где 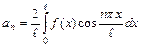 ,
, 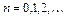 ;
;
2) функция 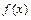 - нечётная, то в точках
- нечётная, то в точках 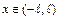 непрерывности функции имеет место разложение
непрерывности функции имеет место разложение  , где
, где 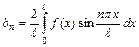 ,
, 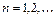 .
.
Если функция 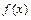 задана только в интервале
задана только в интервале 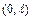 , то её можно продолжить в интервал
, то её можно продолжить в интервал 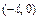 либо как чётную, либо как нечётную, а затем разложить её в интервале
либо как чётную, либо как нечётную, а затем разложить её в интервале 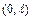 в неполный ряд Фурье по синусам или по косинусам.
в неполный ряд Фурье по синусам или по косинусам.
|
|
|
В задачах 8.194-8.202 разложить следующие функции в ряд Фурье в интервале 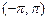 :
:
8.194 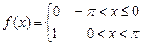 . 8.195
. 8.195 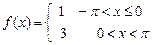 .
.
8.196 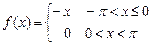 . 8.197
. 8.197 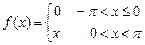 .
.
8.198 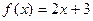 . 8.199
. 8.199 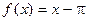 . 8.200
. 8.200 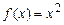 .
.
8.201 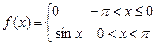 . 8.202
. 8.202 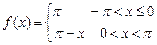 .
.
В задачах 8.203-8.206 разложить функции в ряд Фурье в интервале 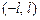 :
:
8.203 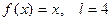 . 8.204
. 8.204 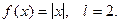
8.205 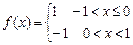 . 8.206
. 8.206 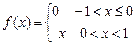 .
.
В задачах 8.207-8.210 разложить функции в неполные ряды Фурье в интервале 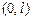 : а) по косинусам, б) по синусам.
: а) по косинусам, б) по синусам.
8.207 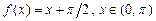 . 8.208
. 8.208 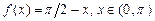 .
.
8.209 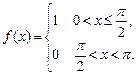 8.210
8.210 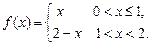
Функция 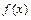 называется абсолютно интегрируемой на
называется абсолютно интегрируемой на 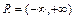 , если
, если 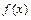 интегрируема на любом отрезке числовой прямой, и существует несобственный интеграл
интегрируема на любом отрезке числовой прямой, и существует несобственный интеграл 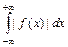 .
.
Если функция 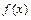 на любом отрезке числовой прямой кусочно-монотонна и непрерывна, за исключением, быть может, конечного числа точек разрыва первого рода, а также абсолютно интегрируема на
на любом отрезке числовой прямой кусочно-монотонна и непрерывна, за исключением, быть может, конечного числа точек разрыва первого рода, а также абсолютно интегрируема на 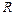 , то в каждой точке
, то в каждой точке 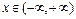 , в которой
, в которой 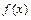 непрерывна, функция представляется интегралом Фурье
непрерывна, функция представляется интегралом Фурье 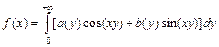 , где
, где 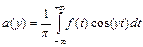 и
и 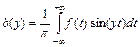 . В точках разрыва функции
. В точках разрыва функции 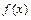 имеет место равенство
имеет место равенство 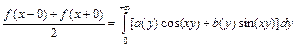 .
.
В частности, если: 1) функция 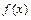 - чётная, то в точках непрерывности функции имеет место равенство
- чётная, то в точках непрерывности функции имеет место равенство 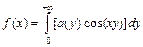 , где
, где 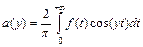 ; 2) функция
; 2) функция 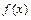 - нечётная, то в точках непрерывности функции имеет место равенство
- нечётная, то в точках непрерывности функции имеет место равенство 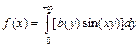 , где
, где 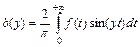 .
.
Если функция 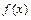 задана только в интервале
задана только в интервале 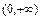 , то её можно продолжить в интервал
, то её можно продолжить в интервал 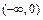 либо как чётную, либо как нечётную, а затем представить её в интервале
либо как чётную, либо как нечётную, а затем представить её в интервале 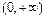 неполным интегралом Фурье по синусам или по косинусам.
неполным интегралом Фурье по синусам или по косинусам.
В задачах 8.211-8.216 представить в интервале 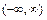 интегралом Фурье, следующие функции:
интегралом Фурье, следующие функции:
8.211 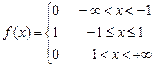 . 8.212
. 8.212 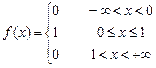 .
.
8.213 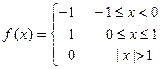 . 8.214
. 8.214 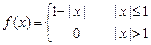 .
.
8.215 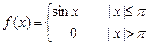 . 8.216
. 8.216 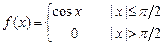 .
.
В задачах 8.217-8.218 функцию 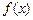 в интервале
в интервале 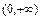 представить интегралом Фурье, продолжив её нечётным образом на интервал
представить интегралом Фурье, продолжив её нечётным образом на интервал 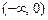 .
.
8.217 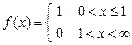 . 8.218
. 8.218 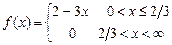 .
.
В задачах 8.219-8.220 функцию 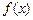 в интервале
в интервале 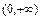 представить интегралом Фурье, продолжив её чётным образом на интервал
представить интегралом Фурье, продолжив её чётным образом на интервал 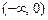 .
.
|
|
|
8.219 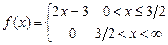 . 8.220
. 8.220 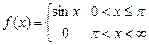 .
.
 2015-03-20
2015-03-20 438
438







