Метод парных сравнений, как правило, используется при небольшом количестве объектов сравнения при наличии подробной информации о них. Он предполагает определение результата оценки по скорректированной стоимости одного (базового) объекта сравнения. В качестве базового объекта сравнения принимается аналог, требующий наименьшую поправку. Это уменьшает влияние ошибок, сделанных в процессе корректировок. Кроме того, отбирается объект, содержащих наименьшее число допущений.
Метод статистического анализа используется при большем количестве объектов сравнения. Скорректированные стоимости объектов сравнения рассматриваются как статистическая выборка. При этом учитывается, что рыночная стоимость определяется как наиболее вероятная цена, по которой может быть продан объект оценки. С точки зрения теории вероятностей наиболее вероятной реализацией случайной величины является ее мода, то есть значение дискретного закона распределения, которому соответствует наибольшая вероятность, или точка максимума плотности непрерывного закона распределения. Исходя из этого рассматриваемая статистическая выборка подвергается следующим процедурам:
- анализ однородности выборки и выявление "выбросов", исключение указанных значений;
- группировка выборки (если ее объем достаточен для такой процедуры) и установление эмпирического закона распределения;
- проверка гипотезы о нормальном распределении генеральной совокупности, если эту гипотезу позволяют выдвинуть результаты построения эмпирического закона распределения;
- если подтверждается гипотеза о нормальном распределении генеральной совокупности, определение выборочной оценки моды генеральной совокупности как среднего арифметического, так как в случае такого распределения мода равна математическому ожиданию;
- если гипотеза о нормальном распределении отвергается, производится корректировка выборочных данных с целью ее приведения к нормальному закону;
- после такой корректировки определяется выборочная оценка математического ожидания скорректированной выборки;
- выборочная оценка моды генеральной совокупности определяется как скорректированная в обратном порядке средняя скорректированной выборки;
- если не удается привести выборку к нормальному закону распределения, оценка моды генеральной совокупности определяется как выборочная оценка данного показателя по сгруппированной исходной выборке;
- если результатом оценки является интервал стоимости, определяется доверительный интервал выборочной оценки моды.
Проверка на "выбросы" выборок объемом до 25 вариант осуществляется следующим образом:
1. Выборка сортируется (для проверки минимального значения – по возрастанию, для максимального значения – по убыванию).
2. Определяется расчетное значение критерия по формуле:
Выборки 3 – 7 единиц:
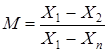 ,
,
где 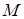 - расчетное значение критерия "выбросов";
- расчетное значение критерия "выбросов";
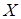 - соответствующая варианта отсортированных выборки.
- соответствующая варианта отсортированных выборки.
Выборки 8 – 10 единиц:
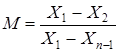 .
.
Выборки 11 – 13 единиц:
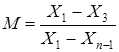 .
.
Выборки 14 – 25 единиц:
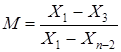 .
.
3. Расчетное значение критерия сравнивается с критическим уровнем, который зависти от принятого уровня значимости (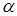 ) (вероятность ошибки первого рода) и объема выборки. Если расчетное значение меньше критического, то проверяемое значение с вероятностью
) (вероятность ошибки первого рода) и объема выборки. Если расчетное значение меньше критического, то проверяемое значение с вероятностью 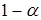 не является выбросом, и его не исключают из выборки.
не является выбросом, и его не исключают из выборки.
При объеме выборки больше 25 единиц используется другой критерий, расчетная величина которого определяется по формуле:
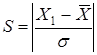 ,
,
где 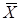 - выборочная оценка математического ожидания (выборочная средняя);
- выборочная оценка математического ожидания (выборочная средняя);
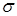 - выборочная оценка среднеквадратического отклонения. Определяется по формуле:
- выборочная оценка среднеквадратического отклонения. Определяется по формуле:
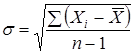 .
.
Порядок проверки на выбросы аналогичен.
При достаточном объеме выборки для ее группировки проверка гипотезы о нормальном законе распределения производится по критерию согласия.
Наиболее известным является критерий согласия Пирсона. Для измерения степени отклонения эмпирического закона распределения от модельного он использует статистику 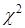 . Процедура проверки проводится по следующим этапам:
. Процедура проверки проводится по следующим этапам:
1. Группировка выборки по 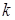 интервалам (необязательно одинаковой длины), таким образом, чтобы интервалы покрывали всю числовую ось.
интервалам (необязательно одинаковой длины), таким образом, чтобы интервалы покрывали всю числовую ось.
2. Определяются частоты 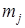 - количество выборочных значений в j-м интервале.
- количество выборочных значений в j-м интервале.
3. На основании выборочных данных строятся статистические оценки неизвестных параметров, от которых зависит модельный закон распределения (для нормального закона – математическое ожидание и среднеквадратическое отклонение).
4. Для каждого интервала вычисляются вероятности 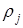 попадания реализации случайной величины с модельным законом распределения и полуучеными ранее параметрами в каждый интервал.
попадания реализации случайной величины с модельным законом распределения и полуучеными ранее параметрами в каждый интервал.
5. Определяется расчетное значение критерия 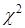 :
:
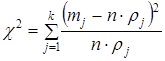 .
.
6. Находится критическое значение статистики 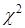 для принятого уровня значимости
для принятого уровня значимости 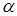 и числа степеней свободы
и числа степеней свободы 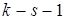 , где
, где 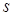 - число параметров, от которых зависит модельный закон распределения.
- число параметров, от которых зависит модельный закон распределения.
7. Если расчетное значение меньше критического, то с вероятностью 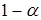 можно принять основную гипотезу о том, что эмпирическое распределение совпадает с модельным.
можно принять основную гипотезу о том, что эмпирическое распределение совпадает с модельным.
Если выборка является малой, проверка гипотезы о нормальном законе распределения осуществляется по системе приближенных критериев.
1. Если коэффициент вариации выборки превышает 0,33, то гипотеза нормальном распределении данных выборки не подтверждается. Дальнейшую проверку при этом не проводят, так как такие распределения должны преобразовываться с целью уменьшения вариации. Коэффициент вариации определяется по формуле:
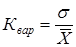
2. Для выборок, имеющих приближенно нормальное распределение, должно выполнятся соотношение:
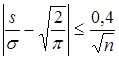
где: 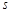 - выборочное среднее абсолютное отклонение (САО);
- выборочное среднее абсолютное отклонение (САО);
3. Проверка по размаху вариации. Размах вариации рассчитывается как разность между наибольшим и наименьшим значением выборки. Определяется критериальное отношение размаха вариации к среднеквадратическому отклонению. Если рассчитанное отношение лежит в пределах границ, гипотеза о нормальном распределении принимается.
4. Абсолютные значения асимметрии и эксцесса выборки не должны совместно значительно (в 2 – 3 раза) превышать свои среднеквадратические отклонения, которые определяются по формулам:
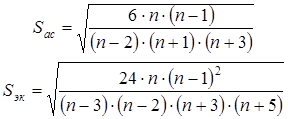
При этом выборочная оценка асимметрии определяется по формуле:
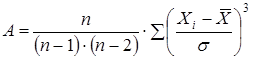 .
.
Выборочная оценка эксцесса определяется по формуле:
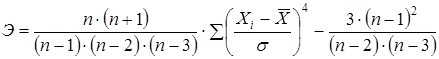 .
.
Если результаты проверки выборки не противоречат всем приведенным условиям, то распределение выборки можно считать приближенно нормальным.
 2015-03-20
2015-03-20 908
908







