Элементы аналитической геометрии в пространстве.
Плоскость в пространстве можно задать различными способами (тремя точками, точкой и вектором, перпендикулярным плоскости, и т.п.). В зависимости от этого рассматривают различные виды ее уравнения.
Дана точка М0(х0, у0, z0) и ненулевой вектор
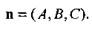
Требуется составить уравнение плоскости, проходящей через точку М0 перпендикулярно к указанному вектору п (этот вектор называют нормальным вектором плоскости).
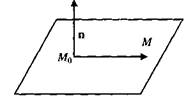
Рассмотрим произвольную точку М(х, у, z) данной плоскости.
Так как вектор М0М =(х-х0, у-у0, z-z0) лежит на плоскости, то он перпендикулярен вектору п (рис.). Следовательно, их скалярное произведение равно нулю, т.е.
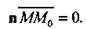
Пользуясь выражением скалярного произведения в получаем искомое уравнение:
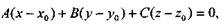
Это уравнение называется уравнением плоскости, проходящей через данную точку перпендикулярно данному вектору.
Подчеркнем, что коэффициентами при х, у, z являются координаты нормального вектора плоскости.
Уравнение первой степени относительно декартовых координат
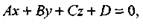
где A, В, С одновременно в нуль не обращаются, т.е.
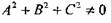
определяет плоскость в пространстве и называется общим уравнением плоскости.
Поскольку это уравнение первого порядка относительно декартовых координат, плоскость является поверхностью первого порядка.
Рассмотрим частные случаи уравнения плоскости, когда один или несколько коэффициентов его обращаются в нуль.
1) D = 0. Уравнение принимает вид
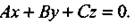
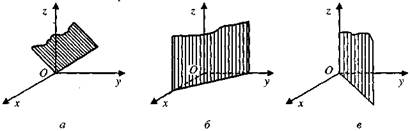
Уравнение определяет плоскость, проходящую через начало координат (рис. а).
2) С = 0. Уравнение принимает вид
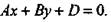
Вектор п = (А, В, 0) перпендикулярен оси Oz и данной плоскости (как ее нормальный вектор), поэтому плоскость, определяемая данным уравнением, параллельна оси Oz (рис. б).
3) С = 0, D = 0. Уравнение
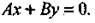
определяет плоскость, проходящую через ось Oz. (рис. в); это следует из двух рассмотренных случаев.
4) В = 0, С = 0. Уравнение
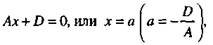
определяет плоскость, параллельную координатной плоскости Oxy вектор п = (А, 0, 0) перпендикулярен оси Оу и оси Ozю
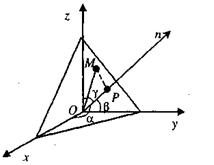
Пусть дана некоторая плоскость. Через начало координат проведем прямую, перпендикулярную этой плоскости, и обозначим буквой Р точку их пересечения (рис.).
Установим на указанной прямой (нормали п)положительное направление, совпадающее с направлением вектора ОР. Обозначим через 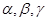 углы, образованные нормалью п с координатными осями Ох, Оу, Oz соответственно, через р - величину вектора ОР., т.е.
углы, образованные нормалью п с координатными осями Ох, Оу, Oz соответственно, через р - величину вектора ОР., т.е.
р = ОР
Уравнение вида
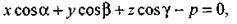
называется нормальным уравнением плоскости.
Общее уравнение плоскости можно привести нормальному уравнению.
Умножив обе части общего уравнения плоскости на число 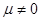 , получим
, получим
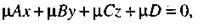
определяющее ту же плоскость, что и исходное уравнение. Выберем 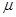 так, чтобы
так, чтобы
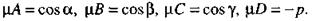
Возводя в квадрат обе части каждого из первых трех уравнений и почленно складывая, находим
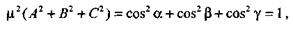
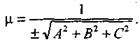
Число 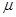 , называется нормирующим множителем. Знак, нужно выбрать противоположный знаку D.
, называется нормирующим множителем. Знак, нужно выбрать противоположный знаку D.
Составим уравнение плоскости, проходящей через три точки 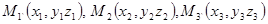 не лежащие на одной прямой. Пусть М(х, у, z) - произвольная точка этой плоскости (рис.).
не лежащие на одной прямой. Пусть М(х, у, z) - произвольная точка этой плоскости (рис.).
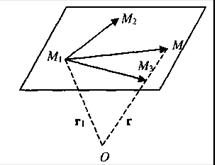
Рассмотрим векторы
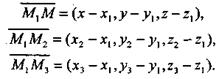
Эти векторы компланарны, поэтому их смешанное произведение равно нулю: 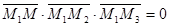 . Принимая во внимание выражение смешанного
. Принимая во внимание выражение смешанного
произведения в координатах, получаем искомое уравнение
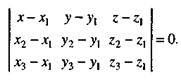
Рассмотрим две плоскости, заданные уравнениями
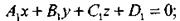
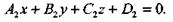
Первая из них имеет нормальный вектор 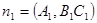 , вторая - нормальный вектор
, вторая - нормальный вектор 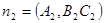 . Плоскости параллельны, когда векторы
. Плоскости параллельны, когда векторы 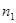 и
и 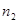 коллинеарны, поэтому необходимое и достаточное условие параллельности двух плоскостей выражается равенствами
коллинеарны, поэтому необходимое и достаточное условие параллельности двух плоскостей выражается равенствами
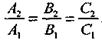
Условие совпадения двух плоскостей выражается равенствами
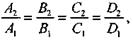
Если условие параллельности не выполнено, плоскости пересекаются. В частности, когда плоскости перпендикулярны, то перпендикулярны и векторы 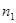 и
и 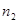 , поэтому их скалярное произведение равно нулю, т.е.
, поэтому их скалярное произведение равно нулю, т.е. 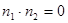 , или
, или
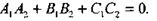
Последнее равенство выражает необходимое и достаточное условие перпендикулярности двух плоскостей.
Пусть даны две плоскости уравнениями. Угол 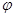 между этими плоскостями равен углу между их нормальными векторами
между этими плоскостями равен углу между их нормальными векторами 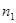 и
и 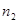 , поэтому
, поэтому
 2015-04-12
2015-04-12 1275
1275