Примеры групп

Пример 5.3. Одна из простейших аддитивных групп состоит из двух элементов, одним из которых является единичный элемент 0. Второй элемент обозначим через 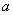. В соответствии с G.4 должен существовать обратный элемент, такой, что 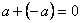. Значит, 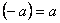, и правило сложения записывается в виде: ; ; 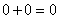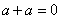. При 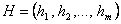имеем правило сложения по модулю .

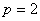Пример 5.4. Совокупность всех действительных чисел образует группу относительно операции обычного сложения. Единичным элементом группы (нулем) является число 0.

Пример 5.5.Совокупность всех действительных чисел без нуля образует мультипликативную группу. Единичным элементом при этом является 1, а обратным – число .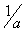

Пример 5.6.Совокупность двоичных 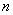-символьных комбинаций образует группу из 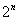элементов, если в качестве групповой операции используется посимвольное сложение по модулю 2. Так, если 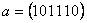, , то 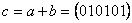. Единичным является элемент 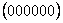, а обратный элемент равен самому элементу, т.к. .

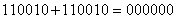Пример 5.7. Полная система вычетов по модулю 6 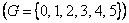является группой с операцией сложения по модулю 6. Единичным элементом этой группы является 0, а обратный элемент находится из равенства 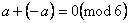. Так, если 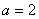, то 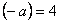и т.д.

Все рассмотренные в примерах группы являются абелевыми.

Теорема 5.1.Группа содержит один единичный элемент, и каждый элемент группы имеет единственный обратный элемент.

Легко видеть, что в примерах 1 – 5 утверждения теоремы выполняются.

Число элементов в группе называется порядком группы. Если порядок конечен, группа называется конечной, в противном случае – бесконечной группой. В примерах 1.3, 1.6 и 1.7 рассмотрены конечные группы 2-го, 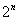-го и 6-го порядков, а в примерах 1.4 и 1.5 – бесконечные группы.