Двойной интеграл по плоской области D, от заданной на ней функции 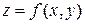 записывают так:
записывают так:
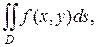 (2.3.1)
(2.3.1)
где ds – мера бесконечно малых элементов области D. Вычисление двойного интеграла сводят к последовательному вычислению двух линейных интегралов по переменным x и y.
При этом область D должна быть правильной.
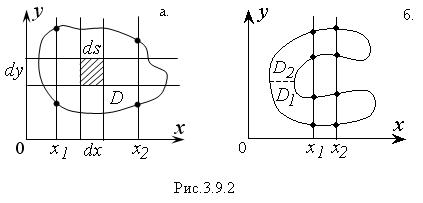
Область D называют правильной, если прямые, параллельные координатным осям, пересекают ее границу не более чем в двух точках (рис. 2.3.1,а). Неправильную область можно разбить на части и представить как объединение правильных областей, например D 1 и D 2 (рис. 2.3.1,б).
|
Плоскую область D правильной формы считают заданной, если известны уравнения ограничивающих ее линий.
Напомним, что элементарные части (элементарные области), на которые разбивают область D при составлении интегральной суммы, были обозначены в круглых скобках:
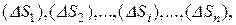
а их меры (площади) тем же символом без круглых скобок:
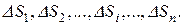
Найдем удобное выражение для меры элемента области – ds.
Для этого разобьем D на элементарные части прямыми, параллельными координатным осям (рис. 2.3.1,а). Тогда мера элементарной части будет равна площади прямоугольника:
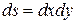
и двойной интеграл (2.3.1) можно записать так:
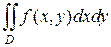 (2.3.2)
(2.3.2)

Пусть уравнение линии, ограничивающей правильную область D известно. Найдем пределы изменения переменных х и у внутри этой области. Для этого спроектируем ее крайние точки А и В на ось Ох (рис.2.3.2). Получим отрезом [ a,b ], в пределах которого изменяется переменная х внутри D.
Далее, заметим, что точки А и В делят на две части линию, ограничивающую область D.
Пусть уравнения этих линий: у 1(х) и у 2(х), следовательно, переменная у внутри плоской области D изменяется от своих значений на линии у 1(х) до значений на линии у 2(х). В результате двойной интеграл (2.3.2) будет равен:
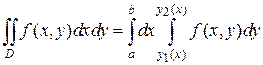 (2.3.3)
(2.3.3)
Из формулы (2.3.3) следует, что вычисление двойного интеграла свелось к последовательному вычислению двух линейных интегралов. Внутренний интеграл берут по переменной y, при этом x – считают постоянной. После нахождения первообразной и подстановки пределов во внутреннем интеграле остается одна переменная x, по которой вычисляют внешний интеграл.
Порядок интегрирования в выражении (2.3.3) можно менять местами. Чтобы внешний интеграл вычислялся не по x, как следует из формулы (2.3.3), а по переменной y, нужно область D спроектировать на ось Оy. Тогда проекции ее крайних точек дадут постоянные пределы во внешнем интеграле для y. Внутренний же интеграл следует вычислять по переменной x, при этом пределы у этой переменной будут зависеть от у.
Таким образом, у внешнего интеграла в обоих случаях пределы постоянны, они равны проекциям крайних точек области на соответствующую координатную ось.
Последовательное вычисление двух линейных интегралов называют двукратным интегрированием.
Следует отметить, что основная трудность при сведении двойного интеграла к двукратному заключается в расстановке пределов во внутреннем интеграле, которые в большинстве случаев переменные. Поэтому сначала строят область D и выбирают координатную ось, на которую проектируют область. Затем находят проекции (α,b) крайних точек области на эту ось и по чертежу определяют переменные пределы для внутреннего интеграла.
Пример 1. Расставить пределы изменения переменных х и у в двойном интеграле:
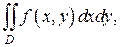
если область D ограничена линиями у 1 = х 2 и у 2 = 6 – х.
Решение. Спроектируем построенную область (рис. 2.3.3) на ось Ох.
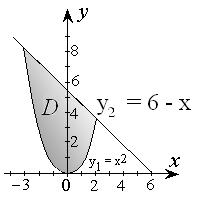
Рис.2.3.3
Точки пересечения графиков функций у 1 = х 2 и у 2 = 6 – х есть крайние точки области.
Найдем их проекции из условия у 1 = у 2:
x 2 = 6 – x или x 2 + x – 6 = 0
Решая квадратное уравнение, получим:
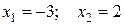 .
.
Таким образом, переменная х в области D пробегает значения от –3 до 2, при этом вторая переменная у изменяется от своих значений на линии
у 1 = х 2 до значений на прямой у 2 = 6 – х.
Следовательно:
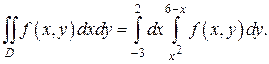
Пример 2. По заданной области расставить пределы
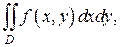
где D: = х2 + у2 < x
Решение. Область D ограниченаокружностью х 2 + у 2 – х = 0 со смещенным центром по оси Ох. Приведем уравнение окружности к каноническому виду. Выделяя полный квадрат по переменной х, получим:
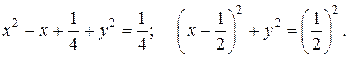
Таким образом, радиус равен 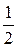 , центр смещен вправо на
, центр смещен вправо на 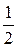
(рис. 2.3.4). Переменная х внутри D изменяется от 0 до 1, вторая переменная у – от своих значений на нижней части окружности (уравнение которой 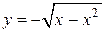 ) до значений на её верхней части, т.е. до
) до значений на её верхней части, т.е. до 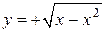 (уравнение окружности решено относительно у).
(уравнение окружности решено относительно у).
Расставляем пределы:
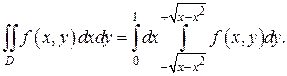
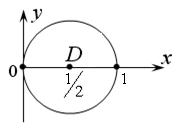
Рис. 2.3.4
Пример 3. Вычислить двойной интеграл
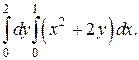
Решение. Пределы изменения переменных внутри области расставлены. Так как они постоянны, область D является прямоугольником со сторонами: по оси Ох от 0 до 1, по оси Оу – от 0 до 2. Вычислим внутренний интеграл по переменной х, считатя у – постоянной.
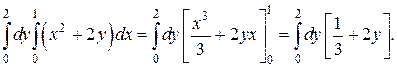
После подстановки пределов вместо переменной х осталась только вторая переменная у. Вычислим внешний интеграл по этой переменной:
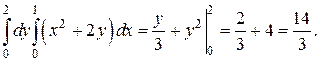
Пример 4. Вычислить двойной интеграл от функции f(x,y) = x – y по области D, ограниченной линиями: y = x 2, y = x.
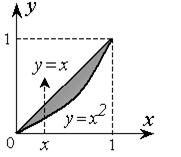 |
| Рис. 2.3.5. |
Решение. Спроектируем построенную область на ось Oх (рис. 2.3.5). Точки пересечения графиков функций y = x 2 и y = x – есть крайние точки области. Найдем их проекции:
x 2 = x; x 1 = 0; x 2 = 1
Таким образом, внутри области D переменная x изменяется от 0 до 1. Пределы изменения второй переменной y будут зависеть от x. Чтобы найти их, проведем прямые параллельные оси Оy, пересекающие область D. Эти прямые для различных значений x входят в область на линии y = x 2 и выходят из области на линии y = x (Рис.2.3.5). Следовательно, переменная y внутри области изменяется от значений на линии y = x 2 до значений на линии y = x.
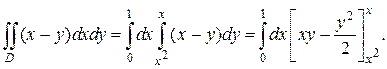
Подставляя вместо y верхний и нижний пределы, получим:
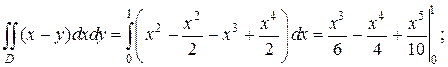
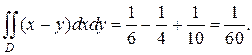
Как отмечалось выше, чтобы внешний интеграл вычислялся по переменной y, нужно область D спроектировать на ось Oy. Найдем проекции крайних точек области на эту ось:
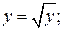
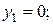
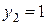 (рис. 2.3.5).
(рис. 2.3.5).
Тогда значения переменной x в области D будут изменятся от ее значений на уравнении прямой x = y до ее значений на уравнении параболы, решенной относительно x: 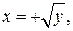 следовательно:
следовательно:
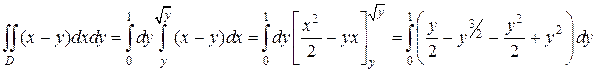
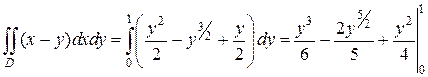
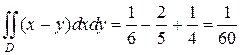
В обоих случаях результат вычислений один и тот же.
Пример 5. Вычислить двойной интеграл 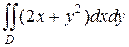 по области D, ограниченной линиями: y = x, y = 0, x + y = 2.
по области D, ограниченной линиями: y = x, y = 0, x + y = 2.
Решение. Область D изображена на рис. 2.3.6. Вид области указывает на то, что внешний интеграл удобнее взять по переменной y. Спроектируем область на эту ось и найдем проекции крайних точек
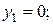
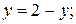
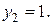
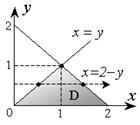 |
| Рис. 2.3.6 |
Переменная x во внутреннем интеграле будет изменяться от своих значений на линии x = y до значений на линии 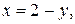 т.е.:
т.е.:
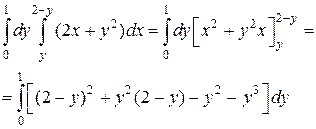
Раскрывая скобки в интеграле, стоящем в правой части последнего равенства и приводя подобные, получим:
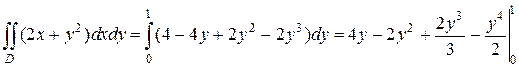
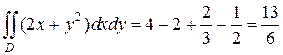
Если область D спроектировать на ось Oх (рис. 2.3.6), то двойной интеграл нельзя будет записать в виде одного двукратного интеграла. Область интегрирования D придется разбить на две части, так как на отрезке [0,1] оси Oх переменная y изменяется от 0 до своих значений на линии y = x, а на отрезке [1,2] – до значений на линии 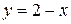 , в результате имеем:
, в результате имеем:
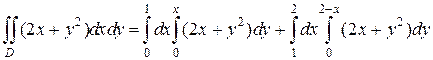
Данный пример показывает, как важно вначале продумать порядок интегрирования.
Задачи для самостоятельного решения. По заданной области расставить пределы в интеграле 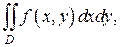
1. D: x ≥ 0, y≥ 0, x+ y≤ 1;
2. D: х2 + y2≤ 4;
D ограничена линиями:
3. у = х 2, х + у = 2, у = 0;
4. у = х 2, х + у = 2, х = 0;
5. у = 4 – х 2, у – х – 2 = 0;
6. у = х, у = 2, ху = 1;
7. у = х 2 – 4 х, у = х;
8. х 2 + у 2 = 4, у – х = 2, у = 0;
9. у = 4 х – х 2, у = х;
10. у = х 3, х = 2, у = –1.
Вычислить двойные интегралы:
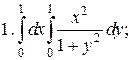
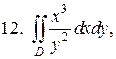
D ограниченая линиями у = х, у = 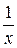 , х = 2;
, х = 2;
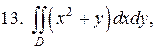
D: у = х 2; 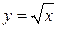
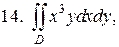
D: у = х 3, х = 2, у = –1;
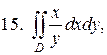
D: у = х, у = 2 х, у = 1.
Практическое занятие 2.4. Тройной интеграл, расстановка пределов, вычисление в декартовой системе координат
Нужно найти значение тройного интеграла от функции трех переменных u = f (x,y,z) по пространственной области W с объемом V:
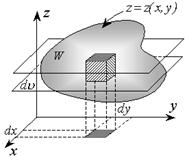 |
| Рис. 2.4.1 |
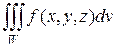 (2.4.1)
(2.4.1)
где dv – мера элемента области (элементарный объем).
Будем считать, что пространственная область (тело) W ограничена одной замкнутой поверхностью, уравнение которой известно
z = z (x, y)
Как и в случае двойного интеграла найдем удобное выражение для меры элемента тела – dv. Для этого разобьем область W на элементарные части плоскостями, параллельными координатным плоскостям (рис. 2.4.1).
Тогда за dv можно принять объем параллелепипеда dv=dxdydz и тройной интеграл примет вид:
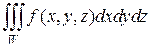 (2.4.2)
(2.4.2)
Вычисление тройного интеграла (2.4.1), подобно двойному, сводят к последовательному вычислению трех линейных интегралов по переменным x, y, z или к трехкратному интегрированию. Найдем пределы изменения переменных x, y, z в заданной пространственной области W (мы уже говорили, что область W считают заданной, если известно уравнение ограничивающей ее поверхности).
Спроектируем тело W на координатную плоскость xOy, в результате получим плоскую область D (рис. 2.4.2). При этом точки касания, проектирующего цилиндра и тела W образуют линию, которая делит поверхность z (x,y), ограничивающую тело W, на две части. Обозначим уравнения этих частей: z 1(x,y) и z 2(x,y) –соответственно.
Очевидно, что переменная z в пределах пространственной области W изменяется от своих значений на поверхности z 1(x,y) до значений на поверхности z 2(x,y). Если проводить прямые, параллельные оси Oz, то они будут входить в данную область на поверхности z 1(x,y) и выходить из нее на поверхности z 2(x,y).
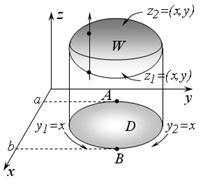 |
| Рис. 2.4.2 |
Далее, спроектируем крайние точки А и В плоской области D на ось Oх, получим отрезок [ α,b ], в пределах которого изменяется переменная x внутри W. И наконец, заметим, что точки А и В делят на две линию, ограничивающую область D. Пусть уравнения этих линий: y 1(x) и y 2(x).
Следовательно, переменная y в пространственной области W изменяется от своих значений на линии y 1(x) до значений на линии y 2(x).
Таким образом, тройной интеграл будет равен трехкратному линейному интегралу вида:
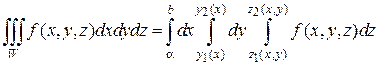 (2.4.3)
(2.4.3)
В формуле (2.4.3) внутренний интеграл берут по переменной z, при этом x и y считают постоянными. После его вычисления и подстановки пределов остаются две переменные x и y. Следующий интеграл вычисляют по переменной y – при условии, что х = const. После его вычисления остается одна переменная x, по которой берут последний внешний интеграл. Пределы внешнего интеграла постоянны. Рассмотрим несколько примеров связанных с вычислением тройных интегралов.
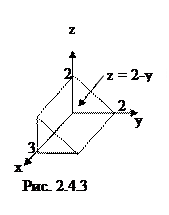
Пример 1. Расставить пределы в тройном интеграле:
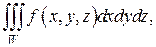
если область W ограничена поверхностями:
z + y = 2; x = 0; x = 3; y = 0; z = 0.
Решение. Область расположение между тремя координатными плоскостями х = 0; у = 0; z = 0 и плоскостью х = 3.
Сверху W ограничена плоскостью z + y = 2, параллельной оси Ох
(рис. 2.4.3). Проекцией области W на координатную плоскость хОу является прямоугольник. Поэтому переменная х внутри W изменяется от 0 до 3, а у – от 0 до 2. Верхний предел для переменной z зависит от у. Значения этой переменной изменяется от 0 до значений на плоскостью z+ y = 2.
Таким образом, тройной интеграл будет равен трехкратному линейному интеграл с пределами
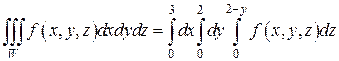
Пример 2. Вычислить интеграл 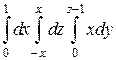
Решение. У внутренних интегралов пределы переменные. Вычислим сначала внутренний интеграл по переменной y, считая xпостоянным
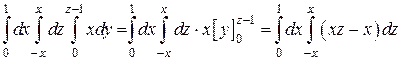
Следующий интеграл берем по переменной z, при этом x = const
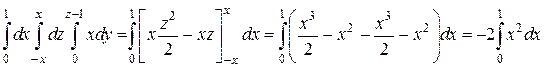
Осталась одна переменная x, вычисляем последний интеграл
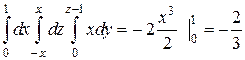
Пример 3. Вычислить тройной интеграл  , где область W ограничена координатными плоскостями: х = 0; y = 0; z = 0, и плоскостью x + y + z = 1.
, где область W ограничена координатными плоскостями: х = 0; y = 0; z = 0, и плоскостью x + y + z = 1.
Решение. Область W представляет собой тетраэдр, ограниченный сверху плоскость x + y + z = 1, которая пересекается с осями координат в точках х = 1; y = 1; z = 1 (Рис.2.4.4). Чтобы найти пределы изменения переменной z в области W, проведем пересекающие тетраэдр прямые, параллельные оси Oz. Эти прямые будут входить в тетраэдр на координатной плоскости z = 0, а выходить из него на плоскости x + y + z = 1.
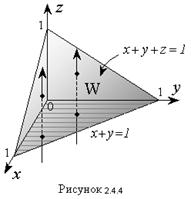 |
Следовательно, значения переменной z внутри области W будут изменяться от 0 до z = 1 – x – y. Таким образом, верхний предел для z непостоянен и зависит от (x, y), т.е. от координат точки на плоскости xОy, через которую проходит пересекающая тетраэдр прямая (Рис 2.4.4.). Проекцией области W на плоскость xOy является треугольник, ограниченный осями координат Ox, Oy и прямой x + y = 1 (Рис.2.4.4). Если его спроектировать на ось Ox, то переменная x внутри треугольника будет изменятся от 0 до 1, а переменная y – от 0 до ее значений на прямой x + y = 1; y = 1 – x. В результате тройной интеграл сводится к трехкратному линейному вида:
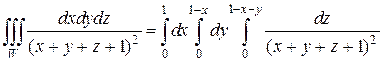
Вычислим сначала внутренний интеграл по переменной z, считая x и y постоянными
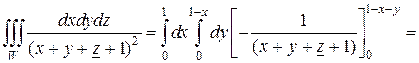
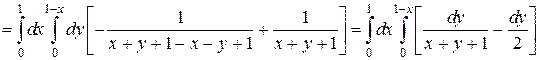
Аналогично найдем средний интеграл по y, считая постоянной x:
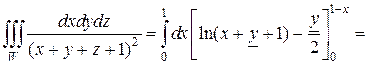
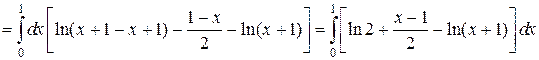
После вычисления среднего интеграла и подстановки пределов осталась одна переменная x. Последний внешний интеграл возьмем по этой переменной, при этом интеграл от логарифма найдем по частям:
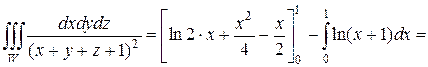
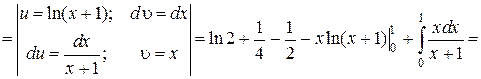
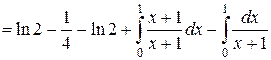
Вычисляя последние два интеграла, окончательно получим:
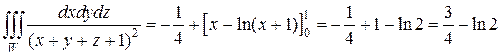
В данном примере верхние пределы у внутреннего и среднего интегралов были переменными. Поэтому изменение порядка интегрирования привело бы к изменению пределов по каждой переменной.
Пример 4. Вычислить тройной интеграл, 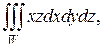 где область W ограничена двумя цилиндрическими поверхностями:
где область W ограничена двумя цилиндрическими поверхностями:
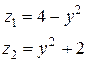
и плоскостями: x = –1; x = 2.
Решение. Цилиндрические поверхности параллельны оси Oх
(рис. 2.4.5). Найдем точки пересечения направляющих линий этих поверхностей из условия 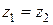 :
:
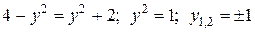
Проекцией области W на плоскость xOy является прямоугольник (Рис.2.4.5). Поэтому пределы изменения для переменных x и y внутри W постоянные:
–1 ≤ x ≤ 2; –1 ≤ y ≤ +1,
а переменная z будет изменяться от значений на поверхности 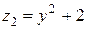 до своих значений на
до своих значений на 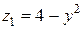 . Данный тройной интеграл сводится к трехкратному линейному интегралу вида:
. Данный тройной интеграл сводится к трехкратному линейному интегралу вида:
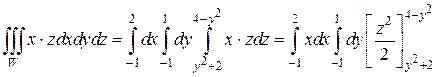
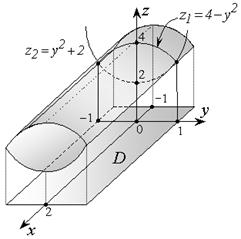
Рис. 2.4.5
Подставляя вместо z пределы и находя оставшиеся интегралы по переменным y и x получим:
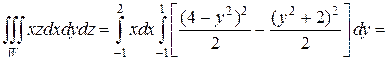
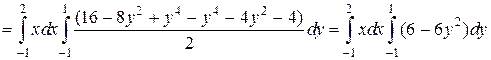
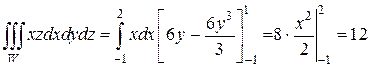
Если область интегрирования W представляет собой параллелепипед с гранями, параллельными координатным плоскостям, то пределы интегрирования будут постоянными во всех трех интегралах. В этом случае интегрирование можно проводить в любом порядке, при этом пределы сохраняются.
Задачи для самостоятельного решения. По заданной области расставить пределы в интеграле 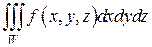 .
.
Область w ограничена поверхностями
1. 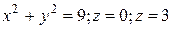 ;
;
2. 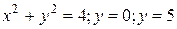 ;
;
3.  ;
;
4. 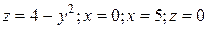 ;
;
5. 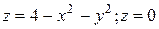 ;
;
6. 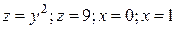 ;
;
7. 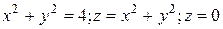 ;
;
8. 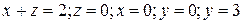 ;
;
9. 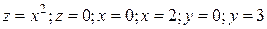 ;
;
10. 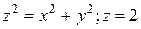 .
.
Вычислить тройной интеграл
11. 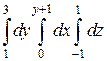 ;
;
12. 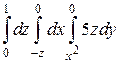 ;
;
13. 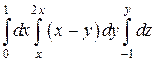 ;
;
14. 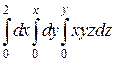 ;
;
15. 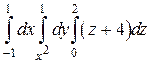 .
.
 2015-04-12
2015-04-12 31140
31140
