Матрицей размерности m x n называется прямоугольная таблица m x n чисел a ij, i=1,..., m, j=1,..., n:
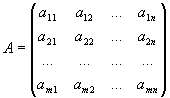
расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n - порядок матрицы).
Линейные матричные операции
По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.
Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.
Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если
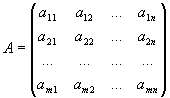 ,
,  ,
,
то произведением матриц A и B, называется матрица
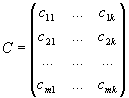 ,
,
элементы которой вычисляются по формуле
c ij =a i1 b 1j + a i2 b 2j +... +a in b nj, i=1,..., m, j=1,..., k.
Произведение матриц A и B обозначается AB, т.е. C=AB.
Действия с матрицами.
Произведение матриц, вообще говоря, зависит от порядка сомножителей. Если AB=BA, то матрицы A и B называются перестановочными.
Проверка перестановочности матриц.
Для квадратных матриц определена единичная матрица - квадратная матрица, все диагональные элементы которой единицы, а остальные - нули:
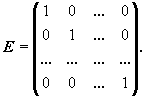
Единичная матрица чаще всего обозначается буквой E или E n, где n - порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы:
AE=EA=A.
Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица - частный случай скалярной матрицы.
Умножение матрицы на матрицы специального вида
Для квадратных матриц определена операция возведения в целую неотрицательную степень:
A 0 =E, A 1 =A, A 2 =AA,..., A n =A n-1 A,....
Возведение матрицы в степень.
Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу A. Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A T:
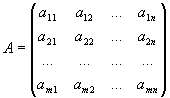 ,
, 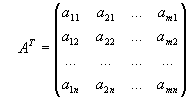 .
.
Вернысоотношения:
(AT)T =A;
(A+B)T=AT +BT;
(AB)T =BT AT.
Квадратная матрица A, для которой A T =A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны.
Квадратная матрица A называется обратимой, если существует такая матрица X, что
AX=XA=E.
Матрица X называется обратной к матрице A и обозначается A -1, т.е.
A A -1 =A -1A=E.
Известно, что если матрица A невырождена (т.е ее определитель отличен от нуля), то у нее существует обратная матрица A -1.
Верно соотношение: (A-1)T =(AT) -1.
Обращение матрицы.
Квадратная матрица U, для которой U -1 =U T, называется ортогональной матрицей.
Свойства ортогональной матрицы:
· Модуль определителя ортогональной матрицы равен единице.
· Сумма квадратов элементов любого столбца ортогональной матрицы равна единице.
· Сумма произведений элементов любого столбца ортогональной матрицы на соответствующие элементы другого столбца равна нулю. Такими же свойствами обладают строки ортогональной матрицы.
Задания:
Пример 1. Действия с матрицами
Вычислим матрицу 2A-BA, где 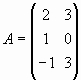 и
и 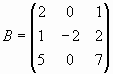 .
.
Пример 2. Проверка перестановочности матриц
Проверим, что матрицы 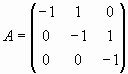 и
и 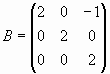 перестановочны, а матрицы А и
перестановочны, а матрицы А и 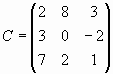 неперестановочны.
неперестановочны.
Пример 3. Умножение матрицы на матрицы специального вида
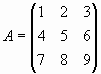
Умножим матрицу на единичную, скалярную и матрицы
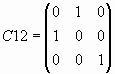 и
и 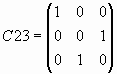 .
.
Пример 4. Возведение матрицы в степень
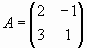
Для матрицы найдем A0, A1, A2.
Пример 5. Обращение матрицы
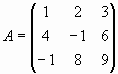
Проверим, что матрица невырождена и найдем матрицу A-1.
Пример 6. Ортогональная матрица
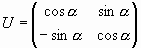
Проверим, что матрица ортогональна.
 2015-04-12
2015-04-12 369
369







