Определение 1. Функция 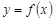 называется непрерывной в точке
называется непрерывной в точке  , если выполняются следующие три условия:
, если выполняются следующие три условия:
1) функция 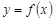 определена в точке
определена в точке  , т.е.
, т.е. 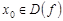 ;
;
2) существует 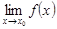 ;3)
;3) 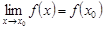 .
.
Если в точке  нарушено хотя бы одно из условий 1–3, то функция называется разрывной в точке
нарушено хотя бы одно из условий 1–3, то функция называется разрывной в точке  , а точка
, а точка  – точкой разрыва.
– точкой разрыва.
Определение 2 (по Коши). Функция  называется непрерывной в точке
называется непрерывной в точке  , если для любого заданного числа
, если для любого заданного числа 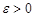 можно найти такое число
можно найти такое число 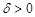 (зависящее от
(зависящее от 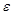 и
и  ), что для всех
), что для всех 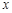 , для которых
, для которых 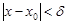 , выполняется неравенство
, выполняется неравенство 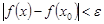 .
.
Символическая запись:
 непрерывна в точке
непрерывна в точке 
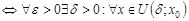
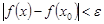 .
.
Пусть 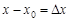 – приращение аргумента, а
– приращение аргумента, а 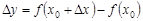 – приращение функции в точке
– приращение функции в точке  . При фиксированном
. При фиксированном  приращение
приращение 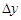 является функцией аргумента
является функцией аргумента 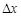 . Можно дать еще одно определение непрерывности функции в терминах приращений.
. Можно дать еще одно определение непрерывности функции в терминах приращений.
Определение 3. Функция  называется непрерывной в точке
называется непрерывной в точке  , если бесконечно малому приращению аргумента
, если бесконечно малому приращению аргумента 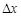 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 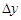 .
.
Определение 3. Функция  называется непрерывной в точке
называется непрерывной в точке  , если бесконечно малому приращению аргумента
, если бесконечно малому приращению аргумента 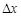 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 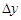 .
.
|
|
|
Теорема РолляПусть функция  удовлетворяет следующим условиям на отрезке
удовлетворяет следующим условиям на отрезке  :
:  определена и непрерывна на
определена и непрерывна на  ;
;  дифференцируема на
дифференцируема на 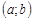 ;
; 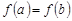 . Тогда существует, по крайней мере, одна точка
. Тогда существует, по крайней мере, одна точка 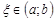 , такая, что
, такая, что 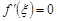 .
.
Теорема 2 (Лагранжа) Если функция  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема на интервале
и дифференцируема на интервале 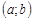 , то существует, по крайней мере, одна точка
, то существует, по крайней мере, одна точка 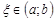 такая, что
такая, что
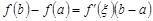 .
.
Теорема Лагранжа называется также теоремой о конечных приращениях, а приведенная формула – формулой Лагранжа. Часто используется следующая запись формулы Лагранжа:
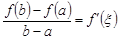 ,
, 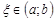 .
.
Если в формуле Лагранжа положить 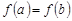 , получим теорему Ролля, т. е. теорема Ролля является частным случаем теоремы Лагранжа. Положим в формуле Лагранжа
, получим теорему Ролля, т. е. теорема Ролля является частным случаем теоремы Лагранжа. Положим в формуле Лагранжа 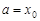 ,
, 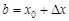 . Тогда она примет вид
. Тогда она примет вид
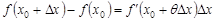 , где
, где 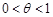 .
.
Данная формула связывает приращения аргумента и функции, поэтому ее называют формулой конечных приращений. Данная формула дает точное выражение приращения функции через вызвавшее его приращение аргумента в отличие от дифференциала функции, который определяет приближенное значение приращения функции: 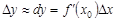 . В приближенных вычислениях приращение функции заменяют чаще дифференциалом, т.е. полагают
. В приближенных вычислениях приращение функции заменяют чаще дифференциалом, т.е. полагают 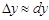 . Формула Лагранжа применяется реже, так как для ее использования необходимо указать точку
. Формула Лагранжа применяется реже, так как для ее использования необходимо указать точку 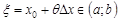 , что, вообще говоря, не всегда удается.
, что, вообще говоря, не всегда удается.
Теорема 3 (Коши) Пусть функции  и
и 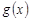 удовлетворяют следующим условиям: непрерывны на отрезке
удовлетворяют следующим условиям: непрерывны на отрезке  ; дифференцируемы в интервале
; дифференцируемы в интервале 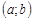 , причем
, причем 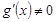
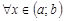 . Тогда существует, по крайней мере, одна точка
. Тогда существует, по крайней мере, одна точка 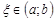 , такая, что
, такая, что
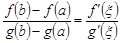 .
.
Если положить в формуле Коши 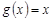 , то все условия теоремы Коши будут выполнены, и формула Коши
, то все условия теоремы Коши будут выполнены, и формула Коши 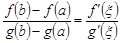 «перейдет» в формулу Лагранжа
«перейдет» в формулу Лагранжа 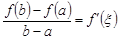 . Таким образом, теорема Лагранжа является частным случаем теоремы Коши
. Таким образом, теорема Лагранжа является частным случаем теоремы Коши
|
|
|
 2015-04-17
2015-04-17 1068
1068








