Непрерывность функции

Дадим два эквивалентных определения непрерывности функции. Предположим, что функция y = f (x) определена на некотором интервале (a, b), и пусть в точке x ₀ Î(a, b) функция принимает значение f (x ₀). Перейдем от значения x ₀ к другому значению x Î(a, b). При этом говорят, что значению x ₀ придано приращение D x = x – x ₀. Разность 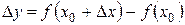между новым и старым значениями функции называется приращением функции в точке x ₀, соответствующим приращению D x.

Определение 1. Функция y = f (x), определенная на некотором интервале (a, b), называется непрерывной в точке x ₀Î(a, b), если бесконечно малому приращению аргумента x ₀ отвечает бесконечно малое приращение функции, т.е. .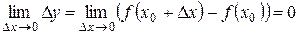

Для второго определения непрерывности нам понадобится понятие односторонних пределов.

2 Число А называется пределом функции y = f (x), при x стремящимся к x ₀ справа, если для любого e > 0 существует такое d > 0, что для любого
x, удовлетворяющего неравенствам 0 < x – x ₀ < d, выполнено неравенство
| f (x) – А | < e. Или, сокращенно, 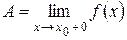, если

.

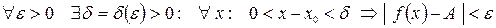2 Число А называется пределом функции y = f (x), при x стремящимся к x ₀ слева, если для любого e > 0 существует такое d > 0, что для любого x, удовлетворяющего неравенствам – d < x – x ₀ < 0, выполнено неравенство
| f (x) – А | < e. Или, сокращенно, 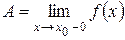, если

.

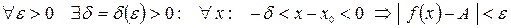Иными словами,

, .

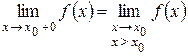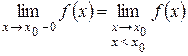Определение 2. Функция y = f (x), определенная на некотором интервале (a, b), называется непрерывной в точке x ₀Î(a, b), если

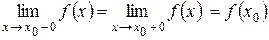(4.10)
Читателям предлагается самостоятельно проверить эквивалентность двух предложенных определений непрерывности.

2 Если 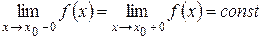, а в точке x ₀ функция
y = f (x) не определена или принимает значение, отличное от односторонних пределов, то говорят, что в точке x ₀ функция y = f (x) терпит разрыв первого рода типа «устранимая особенность».

2 Если 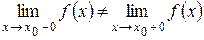, но при этом односторонние пределы существуют и конечны, то говорят, что в точке x ₀ функция y = f (x) терпит разрыв первого рода типа «скачок».

2 Если хотя бы один из односторонних пределов равен бесконечности, или не существует, то говорят, что в точке x ₀ функция y = f (x) терпит разрыв второго рода.

2 Функция называется непрерывной на некотором множестве, если она непрерывна в каждой точке данного множества.

1 Сумма, разность и произведение двух непрерывных функций является непрерывной функцией (на том множестве, на котором непрерывны две данные функции).

1 Частное двух непрерывных функций является непрерывной функцией в тех точках, в которых непрерывны две данные функции, и при этом знаменатель отличен от нуля.

1 Пусть функция t = j (x) непрерывна на некотором множестве D и пусть
Е – множество тех значений функции t = j (x), которые она принимает на множестве D. Если на множестве Е непрерывна некоторая функция y = f (t), то суперпозиция этих функций y = f (j (x)) будет непрерывной на множестве D.

1 Все элементарные функции непрерывны в тех точках, в которых они определены. Например, функции 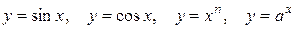непрерывны на всей числовой оси, функция 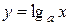непрерывна при 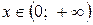, функция 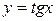непрерывна на любом из интервалов .

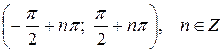Пример 4.11. Исследовать функцию 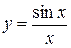на непрерывность.

Функция 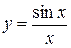, как частное двух непрерывных функций непрерывна во всех точках числовой оси, за исключением точки x = 0. В точке x = 0 функция не определена и, следовательно, терпит разрыв. Исследуем характер разрыва. Для этого найдем односторонние пределы:

.

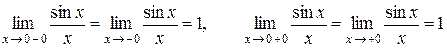Предел слева равен пределу справа, следовательно, в точке x = 0 функция имеет разрыв первого рода типа «устранимая особенность». Если доопределить функцию в точке x = 0 единицей, то она становится непрерывной. То есть

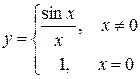– непрерывная функция.

Задача 4.12. Исследовать функцию на непрерывность.

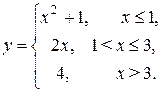
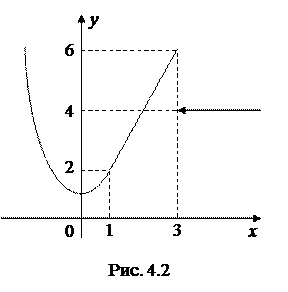Решение. Очевидно, что функция непрерывна на каждом из трех интервалов
x £ 1, 1 £ x < 3 и x ³ 3. Точки x =1 и x = 3 являются подозрительными на наличие разрыва. Найдем односторонние пределы:

,

.

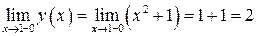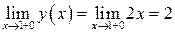Значение функции в точке x =1 равно:
y (1)= 1²+ 1= 2.

Предел слева равен пределу справа, и равен значению функции в точке x = 1, следовательно, в точке x = 1 функция непрерывна.

Исследуем поведение функции в точке x = 3:

.

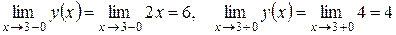Предел слева не равен пределу справа, следовательно, в точке x = 3 функция терпит разрыв первого рода типа «скачок». График функции изображен на
рис. 4.2.

Задача 4.13. Установить характер разрыва функции 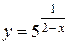в точке x = 2.

Решение. Найдем односторонние пределы в точке x = 2.

При 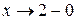знаменатель дроби 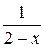стремится к нулю, но остается при этом больше нуля. Следовательно, сама дробь 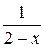стремится к плюс бесконечности. Тогда .

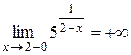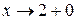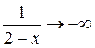При дробь и .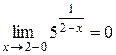

Так как один из односторонних пределов равен бесконечности, то в точке x = 2 функция 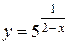терпит разрыв второго рода. Заметим, что в остальных точках функция непрерывна, как суперпозиция непрерывных функций.

Глава 5. Производная функции. Дифференциал