Порядка с постоянными коэффициентами

2 Линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами называются дифференциальные уравнения вида

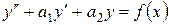. (10.9)

В данном пособии мы ограничимся рассмотрением только линейных однородных дифференцыальных уравнений второго порядка с постоянными коэффициентами, т.е. уравнений вида

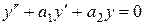. (10.10)

2 Характеристическим уравнением дифференциального уравнения (10.10) называется квадратное уравнеие

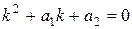, (10.11)

которое получается из уравнения (10.10) путем заиены n – ой производной функции 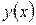на соответствующую степень k.

1 Если уравнение (10.11) имеет два различных действительных корня 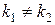, то общим решением дифференциального уравнения (10.10) является

.

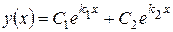1 Если уравнение (10.11) имеет два равных действительных корня 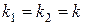, то общим решением дифференциального уравнения (10.10) является

.

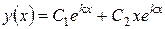1 Если уравнение (10.11) не имеет действительных корней, а имеет два комплексно-сопряженных корня 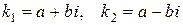(где i ² = – 1), то общим решением дифференциального уравнения (10.10) является

.

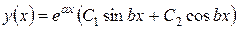Пример 10.8. Найти общее решение дифференциального уравнения:

.

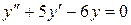Найдем корни характеристического уравнения .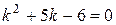

.

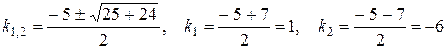Следовательно, общим решением дифференциального уравнения является:

.

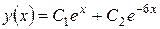Задача 10.9. Решить задачу Коши

.

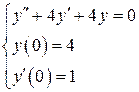Решение. Найдем корни характеристического уравнения .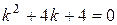

.

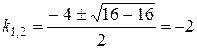Следовательно, общим решением дифференциального уравнения является .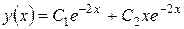

Найдем производную 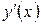и подставим в 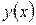и 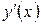начальные условия:

.

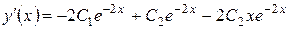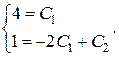
Решая данную систему, мы найдем значения констант 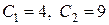, при которых решение дифференциального уравнения удовлетворяет начальным условиям.

Таким образом, мы нашли решение исходной задачи Коши:

.

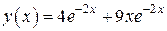Задача 10.10. Найти общее решение дифференциального уравнения

.

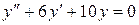Решение. Найдем корни характеристического уравнения .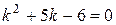

.

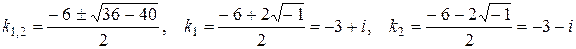Следовательно, общим решением дифференциального уравнения является:

.

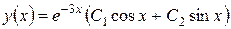Ч А С Т Ь IV Элементы теории вероятностей

Глава 11. Случайные события

§11.1. События

Познание действительности в естественных науках происходит в результате испытаний (эксперимента, наблюдений, опыта).

Испытанием или опытом называется осуществление какого-нибудь определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз.

Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания (опыта).

Таким образом, событие рассматривается как результат испытания.

Пример 11.1. Бросание монеты - это испытание. Появление орла при бросании - событие.

Наблюдаемые нами события различаются по степени возможности их появления и по характеру их взаимосвязи.

Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.

Пример 11.2. Получение студентом положительной или отрицательной оценки на экзамене есть событие достоверное, если экзамен протекает согласно обычным правилам.

Событие называется невозможным, если оно не может произойти в результате данного испытания.

Пример 11.3. Извлечение из урны белого шара, в которой находятся лишь цветные (небелые) шары, есть событие невозможное. Отметим, что при других условиях опыта появления белого шара не исключается; таким образом, это событие невозможно лишь в условиях нашего опыта.

Далее случайные события будем обозначать большими латинскими буквами A,B,C... Достоверное событие обозначим буквой W, невозможное - Ø.

Два или несколько событий называются равновозможными в данном испытании, если имеются основания считать, что ни одно из этих событий не является более возможным или менее возможным, чем другие.

Пример 11.4. При одном бросании игральной кости появление 1, 2, 3, 4, 5 и 6 очков - все это события равновозможные. Предполагается, конечно, что игральная кость изготовлена из однородного материала и имеет правильную форму.

Два события называются несовместными в данном испытании, если появление одного из них исключает появление другого, и совместными в противном случае.

Пример 11.5. В ящике имеются стандартные и нестандартные детали. Берем наудачу одну деталь. Появление стандартной детали исключает появление нестандартной детали. Эти события несовместные.

Несколько событий образуют полную группу событий в данном испытании, если в результате этого испытания обязательно наступит хотя бы одно из них.

Пример 11.6. События из примера 2.4. образуют полную группу равновозможных и попарно несовместных событий.

Два несовместных события, образующих полную группу событий в данном испытании, называются противоположными событиями.

Если одно из них обозначено через A, то другое принято обозначать через`A (читается "не A").

Пример 11.7. Попадание и промах при одном выстреле по цели - события противоположные.

§11.2. Классическое определение вероятности

Рассмотрим в качестве примера испытание, состоящее в двукратном подбрасывании монеты. Каждый из возможных результатов испытания назовем элементарным исходом (элементарным событием). В нашем примере возможны следующие четыре элементарных исхода

, , ,

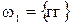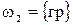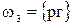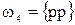
(р - решка, г - герб). Легко видеть,что эти исходы образуют полную группу попарно несовместных событий и они равновозможны. Помимо этих простейших событий с данным испытанием можно связать и более сложные события, в частности,

A= {оба раза монета выпадет одной и той же стороной}

B = { один раз выпадет герб и один раз - решка}

C= {хотя бы один раз выпадет герб}

D= {хотя бы один раз выпадет решка}

Условно эти события можно записать в виде

, , , ,

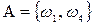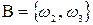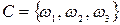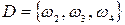где указываются, какие элементарные исходы данного испытания вызывают наступление событий A, B, C и D.

Те элементарные исходы, в которых интересующее нас событие наступает, назовём благоприятствующими этому событию.

Таким образом, событие наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих этому событию. В данном случае разумно считать событие С более возможным, чем событие А, так как благоприятствующих событию С исходов больше, чем событию А. Как видно из приведенного примера, каждое событие обладает определенной степенью возможности наступления, то есть определенной оценкой. Такую оценку события называют вероятностью события.

2 Вероятность события - это численная мера объективной возможности его появления.

По определению, событию можно поставить в соответствие определенное число - его вероятность. Однако приведенное определение не дает формулу для нахождения этого числа. Во многих случаях проблема решается, если применить классическую формулу вероятности, которая дается ниже.

Классическая схема теории вероятностей охватывает те испытания, элементарные исходы (или элементарные события) которых удовлетворяют следующим трем условиям.

1. Элементарные исходы образуют конечное множество: .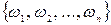

2. Элементарные исходы образуют полную группу попарно несовместных исходов.

3. Элементарные исходы равновозможны.

В условиях 1 - 3 вероятность Р(А) случайного события А определяется как

,

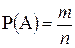где n - число элементарных исходов испытания, а m - число исходов, благоприятствующих событию А. Такое определение вероятности называется классическим.

В рассмотренном выше испытании с двукратным подбрасыванием монеты

n = 4, m_A = m_B= 2, m_C = m_D = 3

и, следовательно,

Р(А) = Р(В) = 2/4 = 1/2,

Р(С) = Р(D) = 3/4.

Классическое определение вероятности долгое время рассматривалось действительно как определение вероятности. В настоящий момент его следует рассматривать не столько как определение, а как метод вычисления вероятностей для испытаний, сводящихся к классической схеме.

Из определения вероятности вытекают следующие ее свойства:

1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n и, следовательно,

.

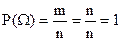2. Вероятность невозможного события равно нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0 и, следовательно,

Р(Ø) .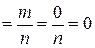

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, а, значит, 0<m/n<1 и, следовательно,

0 < P(A) < 1.

Итак, вероятность любого события удовлетворяет неравенствам

0 £ P(A) £ 1.

Замечание. Ограниченность классического определения вероятности, в частности, заложена в равновозможности исходов. Действительно, даже небольшое усложнение практической ситуации немедленно войдет в противоречие с равновозможностью, которая может рассматриваться скорее как частный случай более общей ситуации.

Приведем теоретико-множественную трактовку понятий теории вероятностей. Ограничимся изложением на языке теории множеств тех понятий, которые рассмотрены выше.

Построение математической модели случайного эксперимента состоит из трех этапов (мы ограничимся конечной схемой с неравновозможными исходами).

I. Первый этап - описание множества элементарных исходов.

Среди всех возможных событий, которые в данном испытании могут произойти, можно выделить множество так называемых элементарных событий ( или элементарных исходов), выделяемых из множества всех событий по следующим признакам:

1) все они взаимно исключают друг друга, и в результате испытаниям обязательно происходит одно из этих событий;

2) каково бы ни было событие А, по наступившему элементарному событию можно судить о том, что наступило или не наступило событие А.

Множество всех элементарных событий, которые могут появиться в испытании, назовем пространством элементарных событий и обозначим .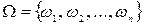

Так, в примере с игральной костью множество элементарных событий состоит из шести элементарных событий 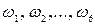, заключающихся в том, что на верхней грани брошенной кости выпало 1,2,…,6 очков соответственно.

II. Второй этап построения модели - описание множества событий.

Для конечных моделей (W - конечное множество) введем следующее определение

2Любое подмножество пространства элементарных исходов называется событием.

Пусть w - наблюдаемый исход эксперимента. Будем говорить, что событие А (А 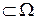) произошло, если 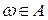. Если же 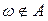, то говорят, что А не произошло.

Событие U = 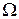называется достоверным. Событие V=Æ называется невозможным. Так в примере с игральной костью U - появление числа очков меньше семи, V - появление отрицательного числа очков.

III. Третий этап построение модели - задание вероятностей на множестве событий. В конечных моделях вероятности событий задаются с помощью следующих определений и аксиом.

2Каждому 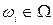соответствует число Р(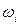), называемое вероятностью элементарного исхода .

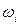Аксиома 1. .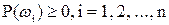

Аксиома 2. .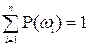

2Вероятностью Р(A) любого события 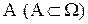называется .

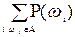Эта схема является обобщением классической схемы. В самом деле, рассмотрим частный случай, когда все элементарные исходы равновозможны, то есть 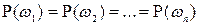. Сумма вероятностей всех элементарных исходов равна единице, следовательно, 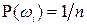, 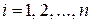. Пусть 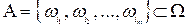. Вероятность Р(A) вычисляется по формуле:

.

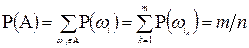Получено классическое определение вероятности.

Аксиомы теории вероятностей позволяют вычислить вероятность любых событий через вероятности элементарных событий. Вопросом о том, откуда берутся вероятности элементарных событий, при аксиоматическом построении теории вероятностей не рассматриваются. На практике они определяются с помощью классического определения или статического определения (см. § 11.3).

В случае, когда 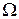- произвольное множество (бесконечное), построение математической модели случайного эксперимента, основано на аксиоматическом определении случайного события и его вероятности. Аксиоматика, предложенная А.Н. Колмогоровым, существенно использует теоретико-множественные понятия. Это довольно сложные построения, которые выходят за рамки данного учебного пособия.