Исследование процессов в системах автоматического управления как процессов передачи информации приводит к необходимости количественно описывать два видимых (качественных) изменения информации при прохождение через звенья системы: изменение величины сигналов и их задержку в силу инерционности элементов.
Совместное описание этих изменений требует адекватного математического аппарата, которым являются функции комплексного переменного. Комплексного - значит сложного, позволяющего отразить одновременно два указанных изменения.
Понятие комплексный связано с мнимой единицей: 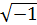 , которая для удобства восприятия и компактности обозначается через j, т.е. j=
, которая для удобства восприятия и компактности обозначается через j, т.е. j= 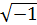 . Введенное обозначение требует запомнить как и необходимые в дальнейших математических выкладках отношения:
. Введенное обозначение требует запомнить как и необходимые в дальнейших математических выкладках отношения:
j= 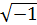 ;
;
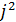 = -1;
= -1;
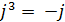 ;
;
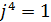 .
.
Представить физический аналог для j не представляется возможным.
Остается вспомнить слова академика Французской академии Анри Пуанкаре о математике:
«Математика дает возможность получать конкретные результаты и этому надо радоваться. Почему? Это никому не известно».
«..получать конкретные результаты..» - это то, что должно вполне удовлетворить инженера, исследующего процессы в системах управления.
Существует две формы записи комплексных чисел: в декартовой и полярной системах координат:
z= x + jy (декартовая) и 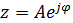 (полярная),
(полярная),
чему соответствуют соответствующие изображения комплексных чисел
на комплексной плоскости
j
y z
0 X
Рис. 23.1. Комплексная плоскость: x = Im z - вещественная часть комплексного числа z, y – Re z - мнимая часть комплексного числа z;
и в полярной системе координат (рис.23.2)
| φ |
A
Рис. 23.2. Полярная система координат: A – модуль (величина вектора z), а φ – аргумент комплексного числа z (угол, характеризующий направление вектора z)
Две формы представления комплексных чисел связаны с выбором той или иной их формы при расчетах.
Сложение (вычитание) комплексных чисел проводится в декартовой форме, а умножение (деление) в полярной форме записи.
Так, имеем z1= x1 +j y1, z2= x2 +j y2, z = z1 + z2= x1 +j y1 +x2 +j y2=
= (x1 +x2)+j(y1 +y2)=x+jy, и результат сложения имеет форму отображаемую в декартовой системе координат.
В другом случае
z1=A1 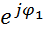 * A2
* A2 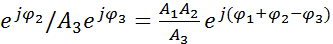 =A
=A 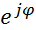
результат отображается в полярной системе координат.
Из проделанного видно, что только применение разных форм к разным арифметическим операциям позволяет приводить результаты к компактным формам, однозначно отображаемым на графиках.
В случае нахождения j в знаменателе домножают и числитель и знаменатель на комплексно сопряженное знаменателю выражение, приводя результат к исходной, отображаемой на графике декартовой системы координат форме.
Так, имеем z = 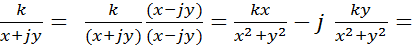 X – jY,
X – jY,
где X = Re z = 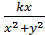 и Y= Im z =
и Y= Im z = 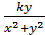 .
.
Параметры вектора z в декартовой системе координат однозначно связаны с параметрами полярной системы (рис. 23.3)
A= 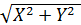 , φ =
, φ = 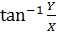
| φ |
Y
A
0 X
Рис. 23.3. Комплексная плоскость, совмещенная с полярной системой координат
В литературе можно встретиться со следующими обозначениями
A = mod z=  , φ = arg z, z =
, φ = arg z, z = 
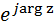 .
.
Наряду с комплексными числами существуют и комплексные функции. Эти функции представляют собой набор значений комплексных чисел, графически представляемых на комплексной плоскости в виде точек, соединенных линиями.
Примером такой функции является
W(jω)= 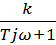 . (23.1)
. (23.1)
Здесь ω независимый аргумент, W(jω) функция аргумента ω.
j лишь подчеркивает комплексный характер функции.
Рассмотрим построение такой функции в различных системах координат.
Для декартовой системы получим
W(jω)= 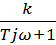 =
= 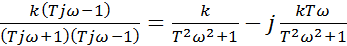 . (23. 2)
. (23. 2)
Введем обозначения
U(ω) = Re W(jω), где U(ω) – вещественная часть функции W(jω),
V(ω)= Jm W(jω), где V(ω) – мнимая часть функции W(jω).
В рассматриваемом случае
U(ω) = 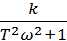 , V(ω) =
, V(ω) = 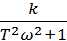
Для полярной системы координат (экспоненциальная форма записи)
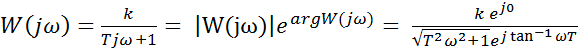 =
=  , (23. 3)
, (23. 3)
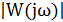 = A(ω) =
= A(ω) = 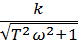 - функция носит название амплитудно-частотной характеристики,
- функция носит название амплитудно-частотной характеристики,
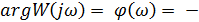
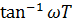 - функция носит название фазочастотной характеристики.
- функция носит название фазочастотной характеристики.
То, что в качестве аргумента функции берется частота, связано с частотными методами исследования систем, рассмотренных в …
В отличии от U(ω) и V(ω), A(ω) и 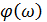 имеют конкретный физический смысл, рассмотренный в ч1, разд.15, и потому наиболее часто используются в расчетах.
имеют конкретный физический смысл, рассмотренный в ч1, разд.15, и потому наиболее часто используются в расчетах.
Графики для 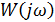 строятся при ω меняющемся от 0 до
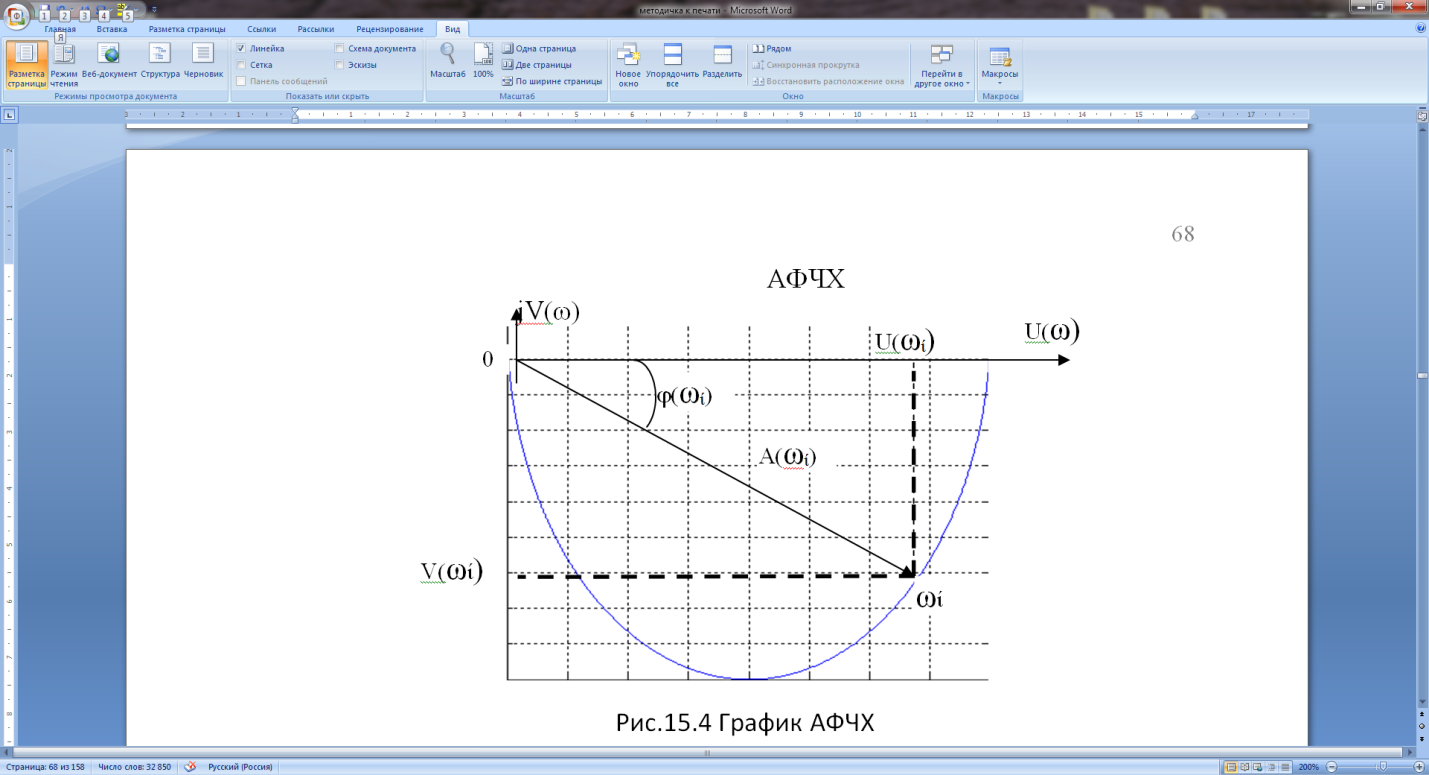
строятся при ω меняющемся от 0 до  . При этом направление построения графика отмечается стрелками, как показано на рис. Данные графики носят название амплитудно-фазачастотных характеристик – АФЧХ.
. При этом направление построения графика отмечается стрелками, как показано на рис. Данные графики носят название амплитудно-фазачастотных характеристик – АФЧХ.
| ω6 |
| ω5 |
ω= 
|
| ω=0 |
| ω6 |
| ω1 |
| ω2 |
| ω5 |
Рис. 23.4. Амплитудно-фазочастотная характеристика – АФЧХ.
 2015-04-17
2015-04-17 585
585








