Соотношение между социально-экономическими явлениями и процессами не всегда можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки.
Так, например, нелинейными оказываются производственные функции (зависимость между объемом произведенной продукции и основными факторами производства - трудом, капиталом и т.п.), функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом) и другие.
Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Примерами нелинейной регрессии по включаемым в нее объясняющим переменным являются следующие функции:
- полиномы разных степеней: 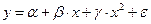 ,
, 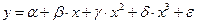 ;
;
- равносторонняя гипербола 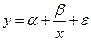 .
.
Примерами регрессий, нелинейных по оцениваемым параметрам, являются:
- степенная 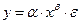 ;
;
- показательная 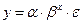 ;
;
- экспоненциальная 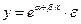 .
.
Для оценки параметров нелинейных моделей используют два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. Второй подход обычно применяется тогда, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.
Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам.
Если модель не линейна по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов.
Например, для параболы второй степени, которую запишем в виде 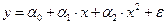 , заменяя переменные
, заменяя переменные 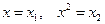 , получим двухфакторное уравнение регрессии
, получим двухфакторное уравнение регрессии 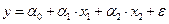 , для оценки которого используется МНК. Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:
, для оценки которого используется МНК. Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:
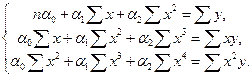
Система содержит 3 уравнения с 3 неизвестными коэффициентами и ее решение может быть произведено любым известным методом (Крамера, Гаусса и т.д.).
Еще один пример – гиперболическая регрессия 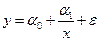 . Линеаризующее преобразование
. Линеаризующее преобразование 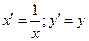 и последующая оценка при помощи МНК приводят к системе
и последующая оценка при помощи МНК приводят к системе
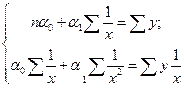 .
.
Следует, однако, отметить и недостаток такой замены переменных, связанный с тем, что оценки параметров получаются не из условия минимизации суммы квадратов отклонений от исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. В связи с этим необходимо определенное уточнение полученных оценок.
Более сложной проблемой является нелинейность по параметрам, так как непосредственное применение МНК для их оценивания невозможно. Однако, если нелинейная модель внутренне линейна, то с помощью соответствующих преобразований может быть приведена к линейному виду. Чаще всего для линеаризации используется логарифмирование.
Примеры внутренне линейных функций и формулы нахождения коэффициентов:
Экспоненциальная регрессия: 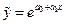 .
.
Линеаризующее преобразование: 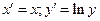 .
.
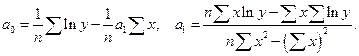
Степенная функция 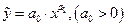 .
.
Линеаризующее преобразование: 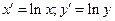 .
.
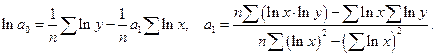
Показательная функция: 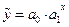 .
.
Линеаризующее преобразование 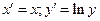 .
.
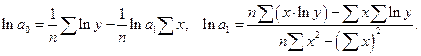
Линеаризующее преобразование 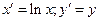 .
.
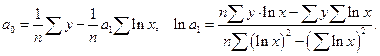
При этом во всех рассмотренных моделях (кроме логарифмической) предполагается, что случайная ошибка 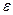 мультипликативно связана с объясняющей переменной
мультипликативно связана с объясняющей переменной 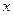 . Если же модель представить, например, в виде
. Если же модель представить, например, в виде 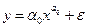 , то она становится внутренне нелинейной и не может быть представлена в линейном виде. Если модель внутренне нелинейна, то используют специальные (итеративные) процедуры оценивания параметров.
, то она становится внутренне нелинейной и не может быть представлена в линейном виде. Если модель внутренне нелинейна, то используют специальные (итеративные) процедуры оценивания параметров.
Из нелинейных функций, которые могут быть приведены к линейному виду, в качестве нелинейной регрессии широко используется степенная функция 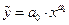 . Это объясняется тем, что параметр
. Это объясняется тем, что параметр 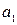 в ней является коэффициентом эластичности, показывающим, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Коэффициент эластичности Э для регрессии вычисляется по формуле
в ней является коэффициентом эластичности, показывающим, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Коэффициент эластичности Э для регрессии вычисляется по формуле
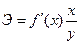
Коэффициент эластичности может быть вычислен и для других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру 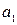 . В других функциях коэффициент эластичности зависит от значений фактора
. В других функциях коэффициент эластичности зависит от значений фактора 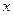 и показывает, насколько процентов изменится
и показывает, насколько процентов изменится 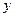 относительно уровня
относительно уровня 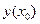 при увеличении
при увеличении 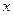 на 1% от уровня
на 1% от уровня 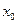 . В силу этого обычно рассчитывают средний показатель эластичности
. В силу этого обычно рассчитывают средний показатель эластичности
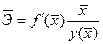 .
.
| Таблица формул расчета коэффициентов эластичности для различных форм зависимости. | ||
| Вид зависимости | Точечный коэффициент эластичности | Средний коэффициент эластичности |
Линейная 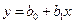 | 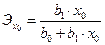 | 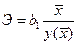 |
Парабола 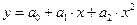 | 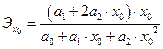 | 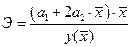 |
Равносторонняя гипербола 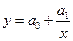 | 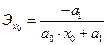 | 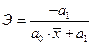 |
Степенная 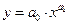 | 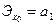 | 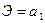 |
Показательная 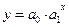 | 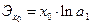 | 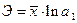 |
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, бессмысленно определять, на сколько процентов изменится заработная плата с ростом стажа рабочего на 1%. В такой ситуации, даже если степенная форма зависимости оказывается наилучшей по формальным соображениям, она не может быть экономически интерпретирована.
Уравнение нелинейной регрессии, так же как и в случае линейной зависимости, дополняется показателями корреляции, а именно индексом детерминации 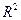 и индексом корреляции
и индексом корреляции 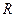 :
:
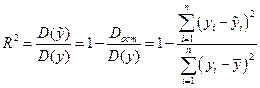 ,
, 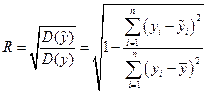 .
.
Величина индекса корреляции 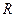 находится в границах от 0 до 1.Чем ближе эта величина к единице, тем теснее связь рассматриваемых признаков.
находится в границах от 0 до 1.Чем ближе эта величина к единице, тем теснее связь рассматриваемых признаков.
Поскольку в расчете индекса корреляции используется соотношение объясненной и общей суммы квадратов отклонений, то 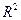 имеет тот же смысл, что и коэффициент детерминации. Оценка существенности индекса корреляции производится так же, как и оценка надежности коэффициента корреляции.
имеет тот же смысл, что и коэффициент детерминации. Оценка существенности индекса корреляции производится так же, как и оценка надежности коэффициента корреляции.
Индекс детерминации 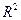 используется для проверки существенности уравнения нелинейной регрессии в целом по F -критерию Фишера:
используется для проверки существенности уравнения нелинейной регрессии в целом по F -критерию Фишера:
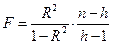 ,
,
где 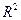 - индекс детерминации;
- индекс детерминации;
n- число наблюдений;
h- число параметров в уравнении.
Индекс детерминации 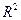 можно сравнивать с коэффициентом детерминации
можно сравнивать с коэффициентом детерминации 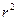 для обоснования возможности использования линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации
для обоснования возможности использования линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации 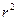 меньше индекса детерминации
меньше индекса детерминации 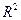 . Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически, если величина
. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически, если величина 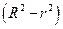 не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различий
не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различий 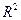 , вычисленных по одним и тем же исходным данным, через t- критерий Стьюдента:
, вычисленных по одним и тем же исходным данным, через t- критерий Стьюдента:
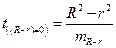 ,
,
где 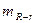 - ошибка разности между
- ошибка разности между 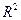 и
и 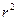 , определяемая по формуле:
, определяемая по формуле:
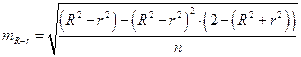 .
.
Если 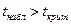 , то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически, если величина
, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически, если величина 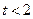 , то различия между
, то различия между 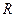 и
и 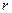 несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.
несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.
 2015-04-01
2015-04-01 3314
3314

 .
.