Задача 2. Нахождение гамильтонова цикла в графе

Гамильтонов цикл – цикл, проходящий в точности по одному разу через каждую вершину графа. Эта задача тесно связана с задачей о коммивояжере: требуется найти маршрут кратчайшей длины, проходящий через все пункты по одному разу и возвращающийся в исходный. Такая задача сформулированная в общем виде часто встречается на практике там, где нужно найти наименьшее упорядочение действий или объектов, например, при планировании локальной сети на предприятии. Для решения поставленной задачи используется метод ветвей и границ, который является центральным среди методов оптимального решения экстремальных комбинаторных задач.

Экстремальной комбинаторной задачей называется задача о нахождении минимума функции y=s(z), z ÎZ – некоторое конечное множество.

Пусть Z(n) – множество всех гамильтоновых контуров p, отвечающих матрице порядка n*n. Зафиксируем некоторую дугу (x_i,x_j) и разобьем множество Z(n) на два непересекающихся подмножества. Z₁⁽¹⁾(n-1) всех контуров, содержащих дугу (x_i,x_j), и Z₂⁽¹⁾(n-1) контуров, не содержащих дугу (x_i,x_j). Тогда получаем две задачи для этих подмножеств, которые с меньшим числом сравниваемых контуров. Для множества Z₁⁽¹⁾(n-1) соответствующая матрица расстояний А₁ получается из А вычёркиванием i–й строки и j-го столбца, дуга (x_i,x_j) исключается, этот процесс называется стягиванием дуги (x_i,x_j). Продолжаем процесс ветвления Z₁⁽¹⁾(n-1) и Z₂⁽¹⁾(n-1), пока не придем к подмножествам, состоящим из одного гамильтонова контура, причем длина этого контура меньше или равна нижних границ всех ранее построенных подмножеств.

Операция приведения над матрицей А состоит в следующем:

1. Из любого элемента каждой строки вычитают минимальный элемент этой же строки (приведение по строкам).

2. Из каждого элемента любого столбца, после приведения по строкам вычитают минимальный элемент этого же столбца (приведение по столбцам).

Полученную в результате матрицу обозначим B и назовем приведенной, B содержит в любых строке и столбце по крайней мере по одному нулевому элементу b_lm =0. Обозначим D = {(l,m) / b_lm =0}. Длина оптимального контура s₀(B) связана с длиной оптимального контура s₀(А) в исходной матрице А соотношением s₀(А)= s₀(B) + (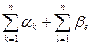), где a_к, к Î(1; n) минимальный элемент k-й строки А, b_е, l Î(1; n) минимальный элемент l-го столбца А, после приведения по строкам. Величина 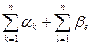= h – константа приведения.

Выбор дуги осуществляется так, чтобы величина а_lm, выражающая увеличение длины контура при невключении в него дуги (l,m), была бы максимальной по всем дугам (l, m), для которых в приведенной матрице B, b_lm = 0, т.е. если 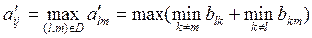, то выбирается дуга (i, j) и b_ml заменяем на бесконечность.

Алгоритм метода ветвей и границ.

I Цикл.

1. Приведение матрицы А.

2. Получение границы множества Z(n): g(z(n)) = h

3. Выбор дуги ветвления.

4. Оценка нижней границы множества Z₂: g(z₂⁽ⁱ⁾) = h_i + a^/_ij

Оценка границы множества Z₁ : g(z₁⁽ⁱ⁾) = h_i-1 + h_i

5. Стягивание матрицы по дуге ветвления.

Процесс повторяем до тех пор, пока множество Z_i не будет содержать только один контур p₁

II. Ветвление множества Z₂^(k), если g(z₂^(k))<s(p₁), тогда получаем контуры p₂, p₃,… p_m, сравниваем их длины между собой и выбираем оптимальный контур.

Пример. Известна матрица стоимостей путешествия между пятью городами:

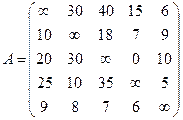. Построить маршрут посещения всех городов с возвращением в исходный пункт наименьший по стоимости.

Решение. Применим алгоритм решения задачи коммивояжёра (метод ветвей и границ).

I 1)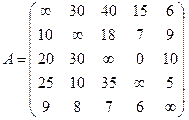

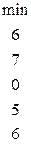
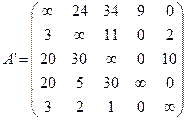
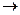
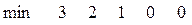
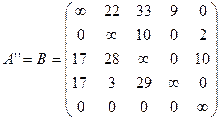- приведённая (редуцированная) матрица

2) h=(6+7+0+5+6)+(3+2+1+0+0)=30=g(z(n))

3) Выбираем дугу ветвления из множества

D={(1;5),(2;1),(2;4),(3;4),(4;5),(5;1),(5;2),(5;3),(5;4)}:

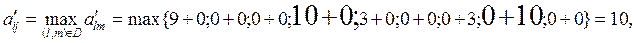
тогда дуга ветвления (3;4) или (5;3). Для определенности примем дугой ветвления (3;4), положим в новой матрице элемент a₄₃=∞.

4) g(z₁⁽ⁱ⁾)=30+10=40.

5) Произведем стягивание матрицы, вычеркнув строку 3 и столбец 4:

1 2 3 5

1 ∞ 22 33 0

2 0 ∞ 10 2

A1= 4 17 3 ∞ 0

5 00 0 ∞

Повторяем цикл I.

1)

1 2 3 5 min 1 2 3 5

1 ∞ 22 33 0 0 1 ∞ 22 33 0

2 0 ∞ 10 2 0 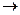A1'= 2 0 ∞ 10 2

A1= 4 17 3 ∞ 0 0 4 17 3 ∞ 0

5 00 0 ∞ 0 5 00 0 ∞

Min 0 0 0 0

1 2 3 5

1 ∞ 22 33 0

2 0 ∞ 10 2

A1''= 4 17 3 ∞ 0

5 00 0 ∞

2) h=0+0=0, тогда g(z(n))=30+0=30

3) Выбираем дугу ветвления из множества

D={(1;5),(2;1),(4;5),(5;1),(5;2),(5;3)}:

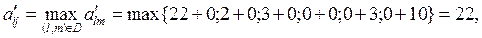
тогда дуга ветвления (1;5), положим в новой матрице элемент a₅₁=∞.

4) g(z₁⁽ⁱ⁾)=30+22=52.

5) Произведем стягивание матрицы, вычеркнув строку 1 и столбец 5:

1 2 3

2 0 ∞ 10

A2= 4 17 3 ∞

5 ∞0 0

Повторяем цикл I.

1) 1 2 3 min 1 2 3

2 0 ∞ 10 0 2 0 ∞ 10

A2= 4 17 3 ∞ 3 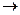A2'= 4 14 0 ∞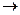

5 ∞0 0 0 5 ∞0 0

Min 0 0 0

1 2 3

2 0 ∞ 10

A2''= 4 14 0 ∞

5 ∞0 0

2) h=3+0=3, тогда g(z(n))=30+3=33

3) Выбираем дугу ветвления из множества

D={(2;1),(4;2),(5;2),(5;3)}:

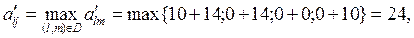
тогда дуга ветвления (2;1), положим в новой матрице элемент a₁₂=∞.

4) g(z₁⁽ⁱ⁾)=33+24=57.

5) Произведем стягивание матрицы, вычеркнув строку 2 и столбец 1:

2 3

A3 = 4 0 ∞

5 0 0

Повторяем цикл I.

1) 2 3 min 2 3 2 3

A3 = 4 0 ∞ 0 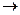A3' = 4 0 ∞ 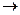A3'' = 4 0 ∞

5 0 0 0 5 0 0 5 0 0

min 0 0

2) h=0+0=0, тогда g(z(n))=33+0=33

3) Выбираем дугу ветвления из множества

D={(4;2),(5;2),(5;3)}:

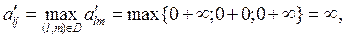
тогда дуга ветвления (4;2) или (5;3).

Итак, выписываем полученные дуги ветвления (3;4), (1;5), (2;1), (4;2), (5;3), получаем искомый гамильтонов цикл 1→5→3→4→2→1наименьшей стоимости 33.