Алгоритм Форда-Фалкерсона

1. Перенумеровать правильно вершины сети Т, отличные от s и t.

2. Построить произвольный поток φ сети Т, например, φ(u)=0 для всех ребер u.

3. Просмотреть пути, соединяющие s и t. Если поток полный, т.е. любой путь из s в t содержит хотя бы одну насыщенную дугу, для которой φ(u)=с (u), перейти к пункту 4.

В противном случае рассмотреть путь μ, все дуги которого ненасыщены и построить новый поток φ`:

φ(u), если u не принадлежит μ;

φ `(u)= φ(u)+k, если u принадлежит μ и k=min{с (u_i)-φ(u_i)},

где u_i- дуги пути μ.

Повторить этот процесс до получения полного потока φ.

4. Присвоить целочисленные метки вершинам сети Т и знаки «+» и «-» дугам по правилам:

а) вершине s присваиваем метку 0;

б) если вершина x_i получила некоторую метку, а вершина y ещё не помечена, тогда вершине y, концевой для дуги, выходящей из x_i, присваиваем метку i, если φ(u_i)<с (u_i), а дуге (x_i; y) присваиваем знак «+» (в этом случае дуга называется аугментальной или увеличивающей);

если вершина x_i получила некоторую метку, а вершина y ещё не помечена, тогда вершине y, начальной для дуги, входящей в x_i, присваиваем метку i, если φ(u_i)>0, а дуге (y; x_i) присваиваем знак «-»;

остальные непомеченные вершины и дуги метки и знака не получают;

в) повторять процесс пункта 4б) до тех пор, пока не прекратится появление новых меток. Если в результате вершина t не получила метки, то поток обладает наибольшей величиной, в противном случае перейти к пункту 5.

5. Рассмотреть последовательность помеченных вершин λ(t, …, s), каждая из которых имеет метку, равную номеру следующей вершины, и последовательность дуг υ, не обязательно являющуюся путем, соединяющих последовательные вершины из λ. Построить новый поток φ`:

φ(u), если u не принадлежит μ;

φ `(u)= φ(u)+1, если u принадлежит μ и имеет знак «+»;

φ(u)-1, если u принадлежит μ и имеет знак «-».

Перейти к пункту 4.

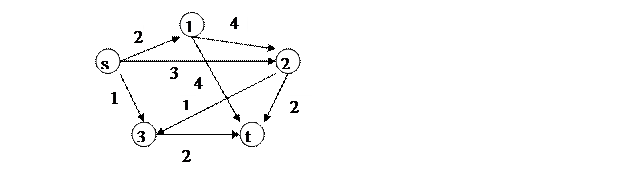
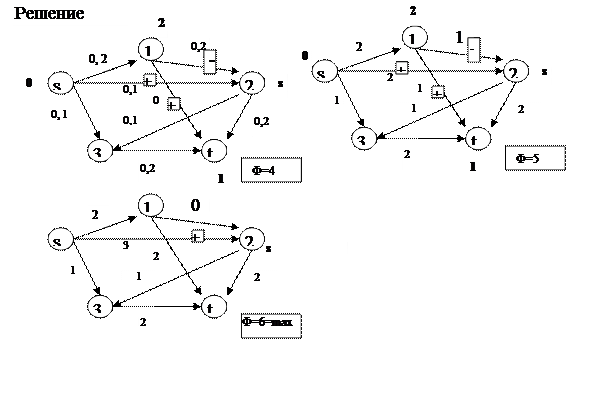
Пример. Оптимизировать поток информации по сети, если известны пропускные способности ее дуг.

Задача 5. Построение многополюсной кратчайшей цепи состоит в нахождении кратчайших путей между всеми парами узлов сети. Длиной d_ij дуги (i;j) считают расстояние между узлами i и j или стоимость потока по дуге. Если узлы i и j не соединены непосредственно, то d_ij:=∞. Для решения задачи используют алгоритм Флойда, основанный на преобразованиях матрицы расстояний D⁽⁰⁾=(d_ij) _nⁿ и матрицы маршрутов R⁽⁰⁾=(j) _nⁿ, согласно которому последовательно выбирают базовые строку и столбец k= 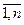и проверяют выполнение условия d_ij ^(k-1)> d_ik ^(k-1) +d_kj ^(k-1), тогда d_ij ^k:= d_ik ^(k-1) +d_kj ^(k-1) и r_ij ^k:= k.

Матрица D⁽ⁿ⁾ указывает кратчайшие расстояния между узлами i и j, матрица R⁽ⁿ⁾ указывает искомую кратчайшую цепь.

Задача 6. Построение о многополюсной цепи с максимальной пропускной способностью состоит в нахождении максимального потока между всеми парами узлов сети. Длиной d_ij дуги (i;j) считают поток между узлами i и j или пропускную способность дуги. Если узлы i и j не соединены непосредственно, то d_ij:=-∞. Для решения задачи используют модифицированный алгоритм Флойда (алгоритм Ху), основанный на преобразованиях матрицы расстояний D⁽⁰⁾=(d_ij)_nⁿ и матрицы маршрутов R⁽⁰⁾=(j) _nⁿ, последовательно выбирают базовые строку и столбец k= 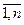и проверяют условие d_ij ^(k-1)< min{d_ik ^(k-1);d_kj ^(k-1)}, тогда d_ij ^k:= max{d_ij ^(k-1); min {d_ik ^(k-1);d_kj ^(k-1)}} и r_ij^k:= k. Матрица D⁽ⁿ⁾ указывает максимальное значение потока между узлами i и j, матрица R⁽ⁿ⁾ указывает искомую цепь.