Задания для самостоятельного решения

Для заданий 1-2 построить вариационный и статистический ряды. Найти эмпирическую функцию распределения, построить график эмпирической функции распределения и полигон частот.

1. 11, 15, 12, 0, 16, 19, 6, 11, 12, 13, 16, 8, 9, 14, 5, 11, 3.

2. 17, 18, 16, 16, 17, 18, 19, 17, 15, 17, 19, 18, 16, 16, 16, 18, 18.

Для заданий 3-4 построить полигон частот и гистограмму.

3.

Границы интервалов	[1;3)	[3;5)	[5;7)	[7;9)	[9;11)	[11;13]

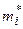4.

Границы интервалов	[5;7)	[7;9)	[9;11)	[11;13)	[13;15)	[15;17]

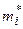Для заданий 5-12 найти оценки числовых характеристик.

5.

xi

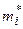6.

xi	-8	-2

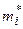7.

xi

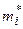8.

xi

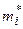9.

xi	-1

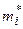10.

Границы интервалов	[61;65)	[65;69)	[69;73)	[73;77)	[77;81)

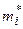11.

Границы интервалов	[0;0,02)	[0,02;0,04)	[0,04;0,06)	[0,06;0,08)

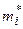12.

Границы интервалов	[-40;-30)	[-30;-20)	[-20;-10)	[-10;0]

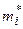13. Для представленной выборки составить интервальный статистический ряд. Для этого ряда построить полигон частот и гистограмму. Найти оценки числовых характеристик.

69 73 70 68 61 73 70 72 67 70

66 70 76 68 71 71 68 70 64 65

72 70 70 69 66 70 77 69 71 74

72 72 72 68 70 67 71 67 72 69

66 75 76 69 71 67 70 73 71 74.

14. По списку на предприятии числится 100 рабочих, которые имеют следующие разряды:

1, 5, 2, 4, 3, 4, 6, 4, 5, 1,

2, 2, 3, 4, 5, 3, 4, 5, 2, 1,

4, 5, 5, 4, 3, 4, 6, 1, 2, 4,

4, 3, 5, 6, 4, 3, 3, 1, 3, 4,

3, 4, 3, 1, 2, 4, 4, 5, 6, 1,

3, 4, 5, 4, 4, 3, 2, 6, 1, 2,

4, 5, 3, 3, 2, 3, 6, 4, 3, 4,

5, 4, 3, 3, 2, 6, 3, 3, 5, 4,

4, 3, 3, 2, 1, 2, 1, 6, 5, 4,

3, 2, 3, 4, 4, 3, 5, 6, 1, 5.

Составить статистический ряд распределения рабочих по разрядам. Построить полигон частот. Найти эмпирическую функцию распределения и построить ее график. Определить средний разряд рабочего, дисперсию и среднее квадратичное отклонение.

15. Имеются следующие данные о числе производственных подразделений на каждом из 100 сельскохозяйственных предприятий:

2,4,5,3,4,6,7,4,5,3,3,4,2,6,5,4,7,2,3,4,

4,5,4,3,4,6,6,5,2,3,4,3,5,6,7,2,4,3,4,5,

4,6,7,2,5,3,5,4,3,7,2,4,3,4,5,4,3,2,6,7,

6,4,3,2,3,4,5,4,3,5,4,3,2,6,4,5,7,5,4,3,

4,5,7,4, 3,4,5,6,5,3,4,2,2,4,3,7,5,6,4,5.

Составить статистический ряд распределения сельскохозяйственных предприятий по числу производственных подразделений на одно хозяйство. Построить полигон частот. Найти эмпирическую функцию распределения и построить ее график. Определить средний разряд рабочего, дисперсию и среднее квадратичное отклонение.

16. Путем устного опроса изучалось качество продукции, выпускаемой фирмой и реализуемой в магазине этой фирмы. Посетители давали оценку качества по десятибалльной шкале. Были получены сводные данные.

Балльная оценка продукции предприятия

Оценка качества продукции, балл	1-2	3-4	5-6	7-8	9-10
Число случаев

Определить средний балл качества продукции, среднее квадратичное отклонение.

17. По данным распределения студентов по результатам сдачи экзаменов определить: средний бал успеваемости студентов по каждому предмету и по всем предметам; дисперсии балла успеваемости по предмету и в целом по всем предметам.

Распределение студентов группы по результатам сдачи экзаменов

Оценка на экзамене	Число студентов, получивших оценку по предметам

18. Работники предприятия сгруппированы по возрасту. Распределение работников предприятия по возрасту представлено в таблице.

Категории работников	Возраст работников, лет	Всего работников
До 30	30-40	40-50	50-60	свыше 60
Рабочие
Руководители
Специалисты
Всего работников	48.

Определить: средний возраст работников предприятия в целом и по отмеченным категориям; дисперсию и среднее квадратичное отклонение возраста по категориям работников и предприятию.

2.2.Практическое занятие по теме «Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ. Выборочный коэффициент корреляции. Определение параметров линейных уравнений регрессии методом наименьших квадратов. Проверка гипотезы о распределении. Критерий Пирсона»

2.2.1. Доверительный интервал для оценки математического ожидания и дисперсии нормального распределения при неизвестном σ.

При малом числе наблюдений точечная оценка в значительной степени случайна, и замена истинного значения параметра на оценку может привести к серьезным ошибкам.

Чтобы дать представление о точности и надежности оценки в математической статистике используют так называемые доверительные интервалы и доверительную вероятность.

Пусть найденная по данным выборки величина ã служит оценкой неизвестного параметра а. Оценка ã определяет параметр а, тем точнее, чем меньше | а − ã |, т.е. чем меньше величина εв неравенстве | а − ã |<ε, ε > 0.

Так как оценка ã − случайная величина, то и разность | а − ã | − случайная величина. Поэтому неравенство | а − ã |<ε, при заданном ε, можетвыполняться только с некоторой вероятностью.

Доверительной вероятностью (надежностью) оценки ã параметра а называется вероятность β, с которой оценивается неравенство | а − ã |<ε.

Доверительную вероятность β назначают достаточно большой (0,9; 0,95; 0,99) такой, чтобы событие с вероятностью β можно было считать практически достоверным. Затем находят такое значение ε, для которого

Р (| а − ã |<ε)= β.

В этом случае диапазон возможных значений ошибки, возникающей при замене параметра а на оценку ã, будет ±ε. Большие по абсолютной величине ошибки будут появляться только с малой вероятностью α = 1−β, которую называют вероятностью риска или уровнем значимости.

Неравенство | а − ã |<εможно записать в виде

− ε < а − ã < εили ã − ε < а < ã + ε.

Доверительным интервалом называется интервал (ã − ε; ã + ε ), который покрывает неизвестный параметр а с заданной надежностью β. Доверительный интервал также можно рассматривать как интервал значений параметра а, совместимых с опытными данными и не противоречащих им.

Доверительный интервал для математического ожидания имеет вид:

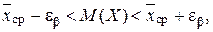(2.2.1)

где 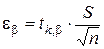и 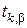−значение статистики Стьюдента для числа степеней свободы k= n- 1и доверительной вероятности β, которые находятся по таблице 4 приложения.

Для построения доверительного интервала для дисперсии используют распределение 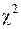. Вид этого закона распределения очень сложен, поэтому значения распределения представлены в таблице 3 приложения. Они зависят от числа степеней свободы и от доверительной вероятности.

Доверительный интервал для дисперсии имеет вид

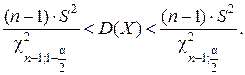(2.2.2)

Пример 1. Произведено 20 опытов над случайной величиной X, распределенной по нормальному закону. Требуется построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности β=0,8, если получены оценки математического ожидания и дисперсии:

S ² = 0,064.

Решение. По таблице 4 приложения находим значение распределения Стьюдента для числа степеней свободы k= n- 1 = 20-1=19и доверительной вероятности β = 0,8:

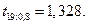
Тогда

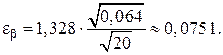
Доверительный интервал для математического ожидания принимает вид

10,78− 0,751 < M(Х) < 10,78 + 0,751,

10,029 < M(Х) < 11,531.

Если доверительная вероятность β=0,8, то уровень значимости α=0,2. По таблице 3 приложения найдем значения распределения :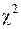

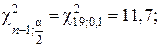
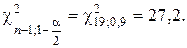
Доверительный интервал для дисперсии:

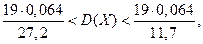
0,0447 < D(X) < 0,1039.