Пусть U – компактное множество, а g 1,…, gm – непрерывные функции, gi: U ®  .
.
Теорема (Гермейер). Пусть x0 – эффективная точка, причем gi (x 0)>0 для всех i= 1,…, m. Тогда существуют положительные числа l1,…l m такие, что 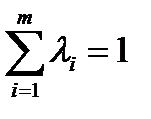 и x 0 является точкой максимума функции
и x 0 является точкой максимума функции 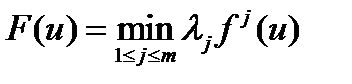 .
.
Доказательство. Положим 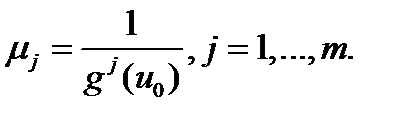 Тогда
Тогда 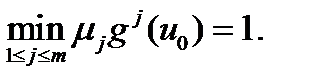
Пусть u – любая точка. Так как точка u 0 – эффективна, найдется номер i, для которого gi (u)£ gi (u 0), или, что то же самое, migi (u)£1. Значит, 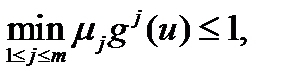 а это означает, что u 0 – одна из точек максимума функции
а это означает, что u 0 – одна из точек максимума функции 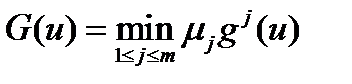 .
.
Остается положить 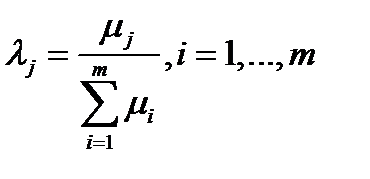 и заметить, что тогда u 0 – одна из точек максимума функции F (u). Теорема доказана.
и заметить, что тогда u 0 – одна из точек максимума функции F (u). Теорема доказана.
К сожалению, нельзя утверждать, что всякая точка максимума функции 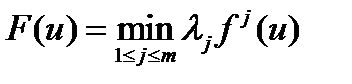 будет эффективной точкой многокритериальной задачи. Пусть U – компактное множество, а g 1,…, gm – непрерывные функции, gi: U ®
будет эффективной точкой многокритериальной задачи. Пусть U – компактное множество, а g 1,…, gm – непрерывные функции, gi: U ®  .
.
Теорема (Гермейер). Пусть u 0 – эффективная точка, причем gi (u 0)>0 для всех i= 1,…, m. Тогда существуют положительные числа l1,…l m такие, что 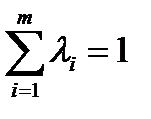 и x 0 является точкой максимума функции
и x 0 является точкой максимума функции 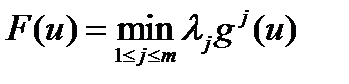 .
.
Доказательство. Положим 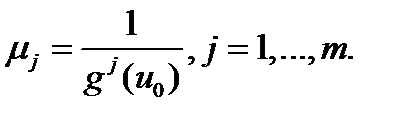 Тогда
Тогда 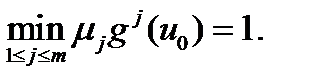
Пусть u – любая точка. Так как точка u 0 – эффективна, найдется номер i, для которого gi (u)£ gi (u 0), или, что то же самое, migi (u)£1. Значит, 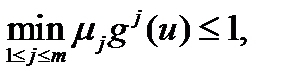 а это означает, что u 0 – одна из точек максимума функции
а это означает, что u 0 – одна из точек максимума функции 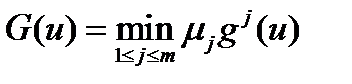 .
.
Остается положить 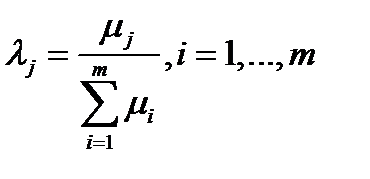 и заметить, что тогда u 0 – одна из точек максимума функции F (u). Теорема доказана.
и заметить, что тогда u 0 – одна из точек максимума функции F (u). Теорема доказана.
К сожалению, нельзя утверждать, что всякая точка максимума функции 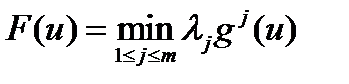 будет эффективной точкой многокритериальной задачи.
будет эффективной точкой многокритериальной задачи.
Пример. Пусть U ={(u 1, u 2): 0£ u 1£1, 0£ u 2£1}, g 1(u)= u 1, g 2(u)= u 2. При 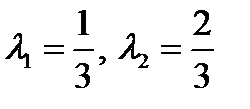 точки максимума функции
точки максимума функции 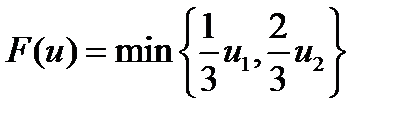 образуют отрезок
образуют отрезок
{(u 1, u 2): u 1=1, 0.5£ u 2£1}, но только одна его точка (1,1) является эффективной.
Теорема. Пусть существуют такие положительные числа l1,…l m, что 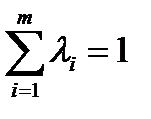 и x 0 является точкой максимума функции
и x 0 является точкой максимума функции 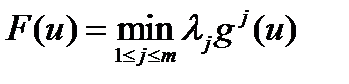 . Тогда точка x 0 является слабо эффективной.
. Тогда точка x 0 является слабо эффективной.
Доказательство. Допустим противное. Тогда найдется такая точка u 1, что gi (u 1)> gi (u 0) для всех i =1,…, m. Но тогда F (u 1)> F (u 0), что противоречит условию.
Пусть теперь множество U выпукло, а функции g 1,…, gm вогнуты.
Теорема (Карлин). Пусть x 0 – эффективная точка. Тогда существуют неотрицательные числа p 1,…, p m такие, что 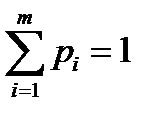 и x 0 является точкой максимума функции
и x 0 является точкой максимума функции 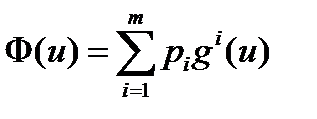 .
.
Доказательство. Не ограничивая общности, можем считать, что gi (u)>0 для всех i= 1,…, m. В силу теоремы Гермейера существуют положительные числа l1,…l m для которых u 0 реализует максимум функции 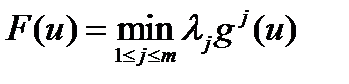 .
.
Тогда (u 0, F (u 0)) является решением задачи математического программирования
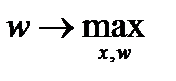 ,
,
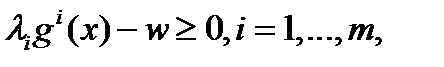
u Î U, w Î  .
.
В силу теоремы Куна–Такера найдутся такие неотрицательные числа a i, i= 1,…, m, для которых (u 0, F (u 0)) будет точкой максимума функции
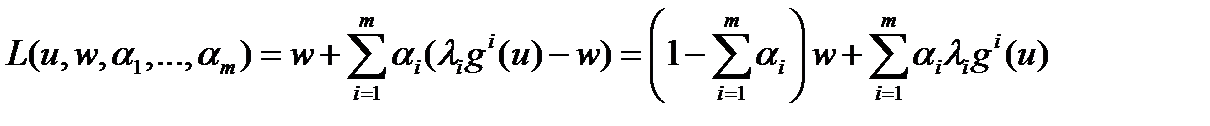
на множестве U ´  . Но это возможно, только если
. Но это возможно, только если
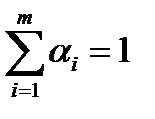 , (*)
, (*)
а тогда u 0 является точкой максимума функции  .
.
Остается заметить, что в силу равенства (*), по крайней мере, одно ai не равно нулю. А тогда мы можем положить 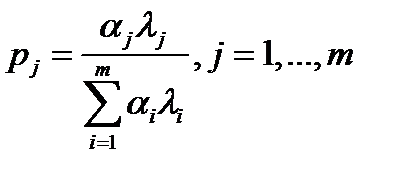 .
.
Теорема. Пусть существуют положительные числа p 1,…, p m такие, что 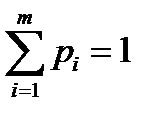 и u 0 является точкой максимума функции
и u 0 является точкой максимума функции 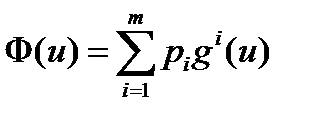 . Тогда точка u 0 является эффективной.
. Тогда точка u 0 является эффективной.
Доказательство. Допустим противное. Тогда найдется такая точка u 1, что gi (u 1)³ gi (u 0) для всех i =1,…, m, причем, по крайней мере, одно из этих неравенств не обращается в равенство. Умножая эти неравенства на pi и суммируя, получим неравенство F(u 1)>F(u 0), что противоречит условию.
Нельзя утверждать, что всякая эффективная точка может быть найдена в результате максимизации функции 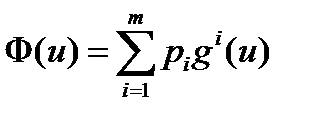 с положительными коэффициентами p 1,…, p m.
с положительными коэффициентами p 1,…, p m.
Пример. Пусть 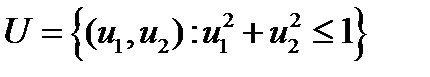 , g 1(u)= u 1, g 2(u)= u 2.Максимум функции
, g 1(u)= u 1, g 2(u)= u 2.Максимум функции 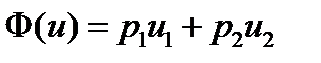 достигается в точке
достигается в точке 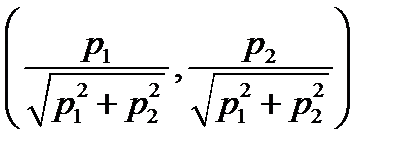 . В то же время, точка (1,0) является эффективной.
. В то же время, точка (1,0) является эффективной.
С другой стороны, при неотрицательных коэффициентах p 1,…, pm, точка максимума функции 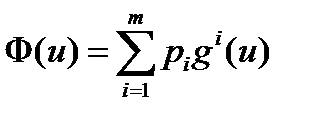 может быть неэффективной в многокритериальной задаче.
может быть неэффективной в многокритериальной задаче.
Пример. Пусть U ={(u 1, u 2): 0£ u 1£1, 0£ u 2£1}, g 1(u)= u 1, g 2(u)= u 2. Точки максимума функции F(u)=1× g 1(u)+0× g 2(u) образуют отрезок {(u 1, u 2): u 1=1, 0£ u 2£1}, а эффективной является только одна точка (1,1) этого отрезка.
Теорема. Пусть существуют неотрицательные числа p 1,…, p m такие, что 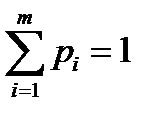 и u 0 является точкой максимума функции
и u 0 является точкой максимума функции 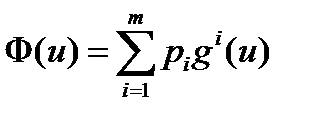 . Тогда точка u 0 является слабо эффективной.
. Тогда точка u 0 является слабо эффективной.
Доказательство. Допустим противное. Тогда найдется такая точка u 1, что gi (u 1)> gi (u 0) для всех i =1,…, m. Умножая эти неравенства на pi и суммируя, получим неравенство F(u 1)>F(u 0), что противоречит условию.
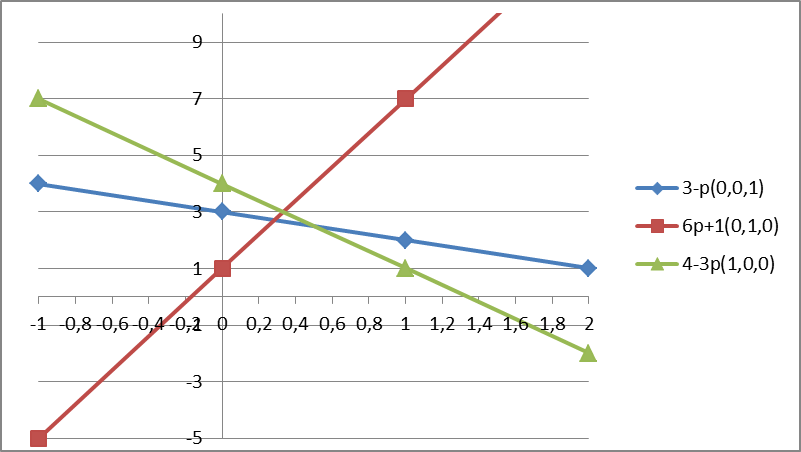
Пример
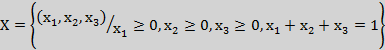
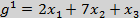
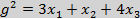
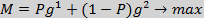
Подставим крайние точки единичного треугольника трехмерного пространства 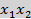
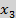
((0,0,1) (0,1,0),(1,0,0)) в систему уравнений 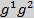 , затем полученные значения
, затем полученные значения  подставим в М и получим 3 прямы
подставим в М и получим 3 прямы
М
Р
Max значение достигается при пересечении прямых 4-3Р и 6р+1, следовательно приравняв их найдет оптимальное значение р
4-3р=6р+1 → р = 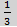 →
→ 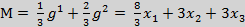
При (1,0,0) М = 
При (0,1,0) М = 3
Значение М в точке (0,1,0) является максимальным и оптимальным по Парето
 2015-04-01
2015-04-01 732
732








