Электромагнитное поле, возникающее в некоторой области пространства, не заполняет его мгновенно, а распространяется с конечной скоростью, зависящей от свойств среды. При распространении периодического процесса с конечной скоростью происходит запаздывание его по фазе. Следствием этого является волновой характер распространения электромагнитного поля.
С целью установления волнового характера электромагнитного поля рассмотрим гармонический во времени процесс в области, не содержащей источников. Кроме того, положим, что среда является идеальным диэлектриком. Для того чтобы учесть эти условия, вектор плотности сторонних токов и токов проводимости в уравнениях (5.6) и (5.7) надо положить равным нулю:
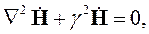
| (5.8) |
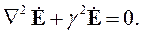
| (5.9) |
В уравнениях (5.8) и (5.9) введено обозначение γ. Это волновое число:
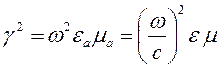
| (5.10) |
Однородные уравнения (5.8) и (5.9) называют волновыми. В такой записи волновое число является действительным, однако может быть и комплексным. Действительное волновое число соответствует среде без потерь.
|
|
|
|
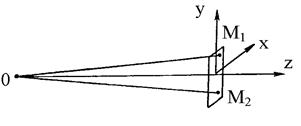
| Рис. 5.1. Плоская волна |
Получим простейшее решение волнового уравнения. Для этого рассмотрим источник, расположенный в безграничной изотропной среде в точке 0 (рис. 5.1). От источника через исследуемую область проведем ось z и рассмотрим площадку, перпендикулярную этой оси. Будем полагать, что площадка расположена так далеко от источника, что любые две ее точки можно считать находящимися на одинаковых расстояниях. В пределах этого допущения отрезки 0М1 и 0М2 равны и параллельны, а точки М1 и М2 по отношению к источнику совершенно равноправны. Следовательно, электромагнитное поле не изменяется при переходе от точки М1 к точке М2 и на всей площадке процесс не зависит от поперечных координат. Поэтому частные производные по этим координатам равны нулю:
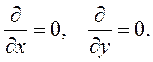
| (5.11) |
Оператор Лапласа существенно упростится:
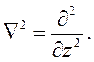
| (5.12) |
Упростятся и волновые уравнения. Например, уравнение (5.8) принимает следующий вид:
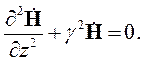
| (5.13) |
Решение такого уравнения хорошо известно:
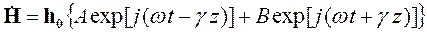
| (5.14) |
| где | h0- орт, указывающий ориентацию вектора напряженности магнитного поля в пространстве, |
| А и В - произвольные коэффициенты, | |
| ωt – γz – фаза процесса в момент времени t на расстоянии z от источника. |
Это решение описывает плоскую однородную волну. Смысл определения «плоская» состоит в том, что в любой плоскости, перпендикулярной направлению распространения, в фиксированный момент времени фаза процесса одинакова. Наблюдатель, двигающийся в такой плоскости, не обнаружит наличия волнового процесса. Эта поверхность равных фаз, в данном случае – плоскость, называется фронтом волны. Определение «однородная» отражает тот факт, что амплитуда волны на поверхности волнового фронта не зависит от координат.
|
|
|
Необходимо обратить внимание на следующее. В формулу (5.14) расстояние входит только в мнимый показатель степени экспоненты. Это значит, что амплитуда плоской волны в среде без потерь не зависит от расстояния.
Мы получили решение волновых уравнений в декартовой системе координат, у которой координатная поверхность – плоскость. Это наиболее простой, но весьма важный случай. Однако для описания всех случаев, встречающихся в практической радиотехнике одного приближения плоской волны недостаточно. Поэтому коротко рассмотрим еще два решения – цилиндрические и сферические волны.
У цилиндрической волны фронт имеет форму кругового цилиндра. Цилиндрические волны обладают осевой симметрией. Они могут возбуждаться, например, бесконечной прямой нитью источников.
Пусть источники расположены вдоль оси z цилиндрической системы координат. В этом случае на расстоянии от оси, значительно превышающем длину волны, справедливо следующее приближенное равенство:
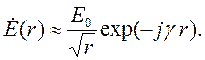
| (5.15) |
Значит, в среде без потерь амплитуда цилиндрической волны обратно пропорциональна корню квадратному из расстояния.
Сферические волны возникают тогда, когда точечный источник возбуждает неограниченное однородное пространство. Зависимость комплексной амплитуды сферической волны от расстояния описывается следующей формулой:
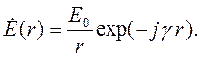
| (5.16) |
Следовательно, амплитуда сферической волны в среде без потерь обратно пропорциональна расстоянию.
Для того чтобы описать электромагнитное поле в естественных условиях, надо знать поведение векторов поля на границе раздела сред с разными электродинамическими характеристиками ε, μ и σ.
 2015-04-01
2015-04-01 2793
2793
