2015-04-08
2202
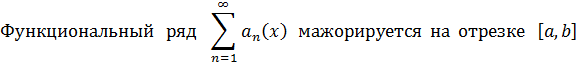
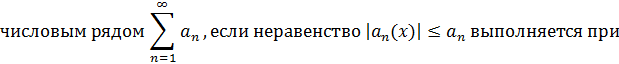
любом n и при всех значениях аргумента x, принадлежащих отрезку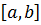 
.
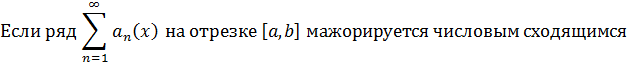
рядом, то исследуемый степенной ряд равномерно сходится на этом отрезке.
Область сходимости степенного ряда обычно находят с помощью признака Даламбера:
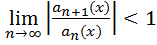(2.1)
или с помощью признака Коши:
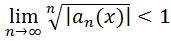(2.2)
Решая неравенства (2.1) или (2.2) находят диапазон изменения аргумента x, при котором неравенства удовлетворяются. Внутри области сходимости ряды сходятся абсолютно и равномерно.
Пример: определить интервал сходимости степенного ряда и исследовать поведение ряда на концах интервала сходимости.
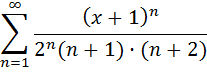
1. Определим интервал сходимости по признаку Даламбера (2.1).
Рассмотрим
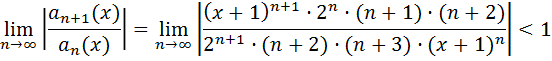
Произведя сокращения, получим:
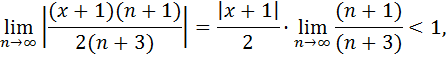
т.к.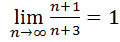 
(по 3-ему замечательному пределу), то получим область сходимости
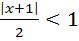или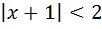 
, т.е.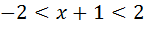 
и окончательно -3 <x< 1. Внутри интервала сходимости (-3; 1) исследуемый ряд сходится абсолютно и равномерно.
2. Исследуем поведение ряда на концах интервала сходимости.
а) Пусть х =-3, тогда на левом конце интервала сходимости получим числовой знакочередующийся ряд
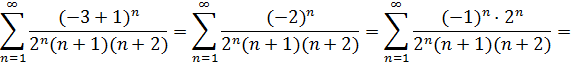
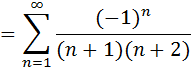
Исследуем полученный знакочередующийся числовой ряд по признаку Лейбница:
; 
; 
; …
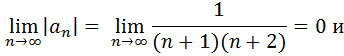
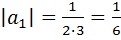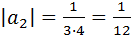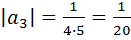Получим, что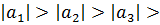 
…- монотонно убывающая последовательность, составленная из модулей членов числового ряда. Следовательно, по признаку Лейбница ряд сходится.
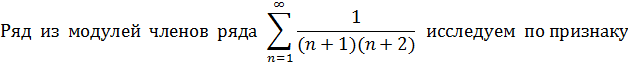
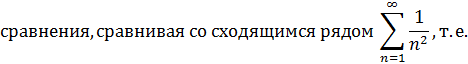
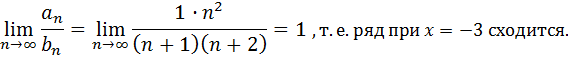
Следовательно, при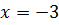 
исходный степенной ряд сходится абсолютно.
б) Пусть х =1, тогда на правом конце интервала сходимости получим знакопостоянный числовой ряд:
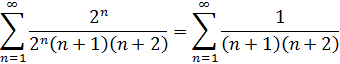
Полученный ряд по признаку сравнения сходится. Ответ: область сходимости [-3;1].
Пример: определить интервал сходимости степенного ряда
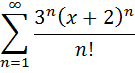
Определим интервал сходимости по признаку Даламбера.
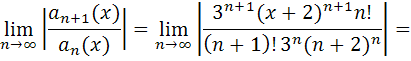
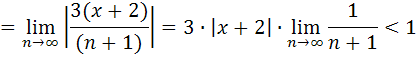
Т.к.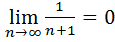 
, следовательно, неравенство справедливо при любых значениях аргумента x, т.е. область сходимости ряда (-∞; +∞) – вся числовая ось.
Пример: найти область сходимости степенного ряда
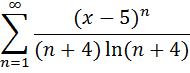
1. Находим область сходимости ряда по признаку Коши:
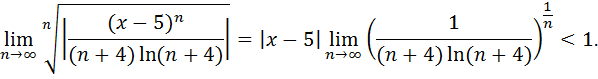
Т.к. предел стремится к единице, то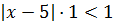 
, т.е. область сходимости 
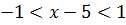или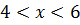 
.
Внутри полученной области сходимости ряд сходится абсолютно и равномерно.
2. Исследуем поведение ряда на концах интервала сходимости.
a) Пусть x =4, на левом конце области сходимости получаем знакочередующийся числовой ряд:
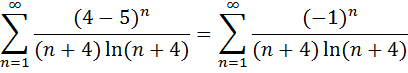
Исследуем знакочередующийся числовой ряд по признаку Лейбница:
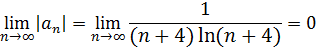
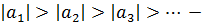монотонно убывающая последовательность, следовательно, по признаку Лейбница ряд сходится.
Исследуем ряд из модулей членов ряда по интегральному признаку Коши.
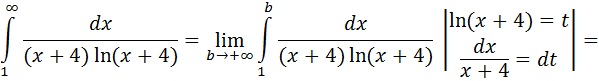
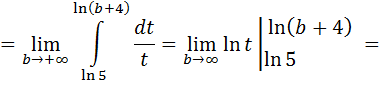
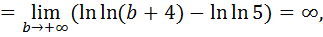
следовательно, ряд из модулей членов ряда расходится. Т.е. при x =4 имеем условную сходимость.
б) Пусть x =6.
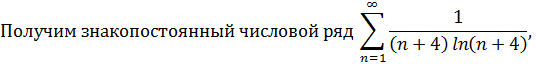
соответствующий ряду из модулей членов исходного ряда. Но по интегральному признаку Коши такой знакопостоянный числовой ряд расходится, т.е. при x =6 исследуемый ряд расходится.
Ответ: область сходимости заданного ряда [4; 6). На левом конце интервала сходимости при x =4 сходимость условная, точка x =6 в область сходимости не входит. Внутри области сходимости (4;6) исследуемый ряд сходится абсолютно и равномерно.
