Более полный и надежный способ оценивания параметров распределений заключается в определении не единственного точечного значения, а интервала, который с заданной вероятностью содержит истинное значение оцениваемого параметра. Для заранее выбранного уровня значимости 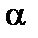 ,
, 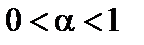 по выборке определяются два числа
по выборке определяются два числа 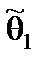 и
и 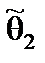 ,
, 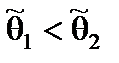 , между которыми с вероятностью
, между которыми с вероятностью 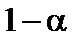 находится неизвестный параметр
находится неизвестный параметр 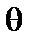 :
: 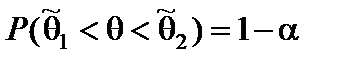 .
.
Число  называется доверительной вероятностью (надежностью),
называется доверительной вероятностью (надежностью), 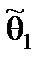 ,
, 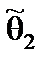 – доверительными нижней и верхней границами. Величины
– доверительными нижней и верхней границами. Величины 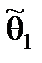 ,
, 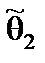 определяются по результатам выборки, следовательно, являются случайными.
определяются по результатам выборки, следовательно, являются случайными.
Если 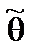 – точечная оценка неизвестного параметра q, то
– точечная оценка неизвестного параметра q, то 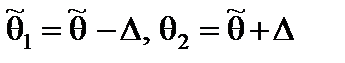 , где
, где 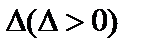 – предельная ошибка (уровень надежности) выборки, которая либо задается заранее, либо вычисляется.
– предельная ошибка (уровень надежности) выборки, которая либо задается заранее, либо вычисляется.
На практике часто используются односторонние доверительные интервалы, которые определяются из условий 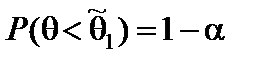 или
или 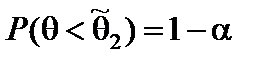 и называются правосторонними и левосторонними соответственно.
и называются правосторонними и левосторонними соответственно.
Длина доверительного интервала, характеризующая точность интервальной оценки, зависит от объема выборки 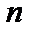 и надежности
и надежности 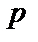 . При увеличении
. При увеличении 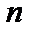 длина доверительного интервала уменьшается, а с приближением надежности к 1 – увеличивается. В качестве
длина доверительного интервала уменьшается, а с приближением надежности к 1 – увеличивается. В качестве 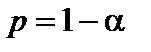 принимают значения 0,9; 0,95; 0,99, что соответствует 90, 95, 99%-ым доверительным интервалам соответственно.
принимают значения 0,9; 0,95; 0,99, что соответствует 90, 95, 99%-ым доверительным интервалам соответственно.
Задача определения доверительного интервала может быть решена только тогда, когда удается найти закон распределения случайной величины, используемой в качестве оценки. В общем случае этот закон зависит от самого неизвестного параметра. Однако иногда удается перейти от оценки 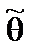 к таким функциям выборочных значений, закон распределения которых зависит только от объема выборки
к таким функциям выборочных значений, закон распределения которых зависит только от объема выборки 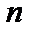 и закона распределения случайной величины и не зависит от неизве-стных параметров.
и закона распределения случайной величины и не зависит от неизве-стных параметров.
Пусть выборка 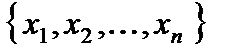 произведена из генеральной совокупности значений нормально распределенной с параметрами
произведена из генеральной совокупности значений нормально распределенной с параметрами 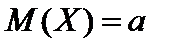 и
и 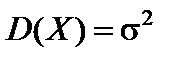 случайной величины
случайной величины 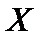 , т.е.
, т.е. 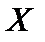 ~
~ 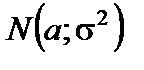 .
.
Доверительный интервал для математического ожидания 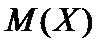 при известной дисперсии
при известной дисперсии 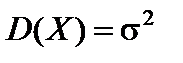 с доверительной вероятностью
с доверительной вероятностью 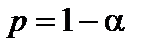 имеет вид:
имеет вид:
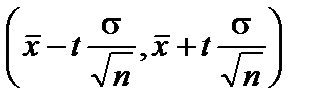 или
или  .
.
Здесь 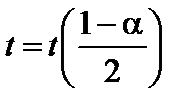 – квантиль порядка
– квантиль порядка 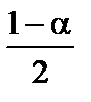 нормального распределения, заданного функцией распределения вероятностей
нормального распределения, заданного функцией распределения вероятностей
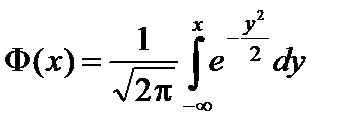 , т. е.
, т. е. 
Выражение 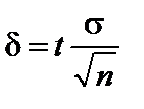 – точность оценки. Из соотношения
– точность оценки. Из соотношения 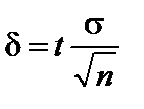 находится минимальный объем
находится минимальный объем 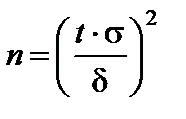 выборки, который обеспечивает заданную точность
выборки, который обеспечивает заданную точность 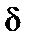 .
.
Число  , как правило, неизвестно, поэтому его заменяют приближенным значением:
, как правило, неизвестно, поэтому его заменяют приближенным значением: 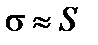 .
.
Пример 7.4. Автомат наполняет пакеты с чипсами. Установлено по выборочным данным, что стандартное отклонение веса пакетов 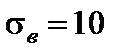 г. Среднее значение веса пакета
г. Среднее значение веса пакета 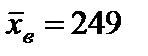 г (при n = 36). В каком интервале с надежностью 95% лежит истинное значение веса, считая что вес подчиняется нормальному распределению
г (при n = 36). В каком интервале с надежностью 95% лежит истинное значение веса, считая что вес подчиняется нормальному распределению 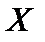 ~ N (m; 10).
~ N (m; 10).
Решение
Для определения 95% доверительного интервала найдем критическую точку 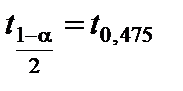 из уравнения
из уравнения 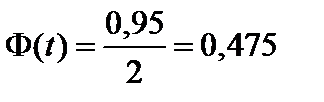 .
.
По таблицам функции Лапласа 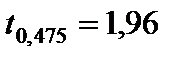 . Тогда доверительный интервал имеет вид
. Тогда доверительный интервал имеет вид 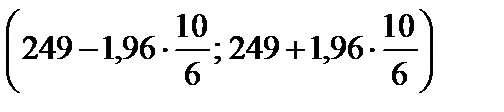 .
.
Тест 7.20. Доверительный интервал для оценки математического ожидания при выборочной средней 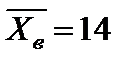 и точности оценки
и точности оценки 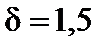 имеет вид:
имеет вид:
1) (12,5; 15,5);
2) (14,5; 17);
3) (0;14);
4) (14; 28).
Вопросы для самоконтроля
1. Какие числовые характеристики выборки относятся к показателям положения?
2. Какие числовые характеристики выборки относятся к показателям разброса?
3. Какой показатель характеризует симметрию распределения?
4. Что называется выборочным средним, выборочной модой, выборочной медианой, выборочной дисперсией?
5. Каким условиям должны удовлетворять точечные оценки?
6. Какие оценки называются интервальными?
7. Что называется доверительной вероятностью?
 2015-04-20
2015-04-20 1847
1847
