Методы упрощения систем

В ходе решения системных задач по разным причинам могут возникать потребности упрощения системы. Такими причинами являются сложность физической интерпретации результатов решения задачи, малый объем наблюдений или недостаточные вычислительные и временные ресурсы.

Известно два основных подхода к упрощению систем: сокращение множества переменных и объединение состояний системы в классы эквивалентности.

В общем виде задача упрощения состоит в следующем. Для системы заданной на множестве переменных X с полным множеством состояний С необходимо найти вариант упрощенной системы на подмножестве переменных X' ⊂ X или подмножестве состояний C' ⊂ C.

При исключении переменных общее число возможных вариантов упрощения равно

Л_X = 2^|X| - 2

Рассмотрим систему из трех переменных X₁, X₂, X₃. Варианты упрощения системы путем исключения переменных приведены на рис.

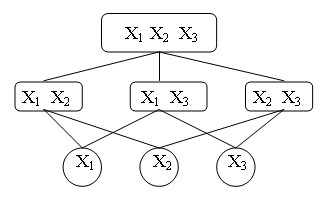
Рис. — Упрощение системы путем исключения переменных

При объединении состояний системы в классы эквивалентности общее число вариантов упрощения равно

Л_C = ∑Лⁱ_|C|

Целью упрощения является смещение уровня сложности системы при сохранении минимума нечеткости. Оба эти условия противоречивы. Поэтому выбор подходящего варианта необходимо производить по близости функций ограничения на полном множестве состояний исходной и упрощенной систем.

Рассмотрим функцию ограничения упрощенной системы. Пусть Х и X₁ ⊂ X', f и f' соответственно множество переменных и функции ограничения на множестве состояний исходной и упрощенной системы. Полное множество состояний С' упрощенной системы есть проекция вида

C' = Пр_X'•C

Поэтому функция ограничения f ' также является проекцией

f' = Пр_Х•f

Рассмотрим пример. Пусть дана система на множестве переменных X₁, X₂, X₃, X₄.В таблице приведено полное множество состояний и значение функций ограничения. Выберем вариант упрощения (X₁ X₂ X₃ X₄) → (X₁ X₂). У упрощенной системы состояние C_i включает состояния C₁, C₂, C₃ исходной системы, состояние C'₂ состояния C₄, C₅, C'₃ состояния C₆, C₇, C₈.

Ci X1 X2 X3 X4 fi           0,2           0,2           0,1           0,1           0,1           0,1           0,1           0,1	C' X1 X2 f'i       0,2+0,2+0,1=0,52       0,1+0,1=0,23       0,1+0,1+0,1=0,34

Полное множество состояний упрощенной системы и значение функции ограничения приведены в табл.

Аналогичным образом может быть найдена функция ограничения в случае упрощения путем объединения состояний системы в классы эквивалентности.

Близости функций ограничения может быть выражена через метрическое расстояние между ними. Существует много разных типов метрический расстояний. Поэтому ограничимся рассмотрением двух следующих модификаций.

Класс расстояний Минковского определяется следующей формулой [].

Структурированная система.

Структурирование системы заданной на множестве переменных Х представляет собой разделение исходного множества переменных на подмножества Xⁱ ⊂ X. Подмножество структурированной системы будет называть подсистемами структурированной системы.

Подмножество структурированной системы должны удовлетворять следующим условиям.

1. Все подмножества задаются на одном параметрическом множестве.
2. Каждое подмножество Хⁱ имеет общие переменные хотя бы с одним подмножеством т.е. справедливо следующее

X¹ ∩ (X₂ ∪ X₃ ∪ X^m) ≠ ∅

X² ∩ (X₁ ∪ X₃ ∪ X^m) ≠ ∅

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _

X^m ∩ (X₁ ∪ X₂ ∪ X^m-1) ≠ ∅

Имеет ряд причин требующих представления системы в виде структурированной. Во-первых нередко формирование системы происходит на множествах наблюдений полученных в разное время и в разных местах. Во-вторых должным образом обоснованная структурированная система может выявлять свойства, которые в явном виде не проявляются в исходной системы. В-третьих высокий уровень сложности системы может потребовать исследования системы по частям. Отсюда вытекают две возможные задачи:

1. Заданы системы на множество [X¹, X², X³,...]. Требуется сформировать структурированную систему и найти соответствующую исходную систему на множестве X = [X¹ ∪ X² ∪ α³ ∪...].
2. Задана система. Требуется найти структурированную систему, которая выявляет равные свойства.

Любая система может иметь множество соответствующих ей структурированных систем.

Пример. Задана система на множестве X = (X₁, X₂, X₃). Соответствующие ей варианты структурированных систем приведены на рис.

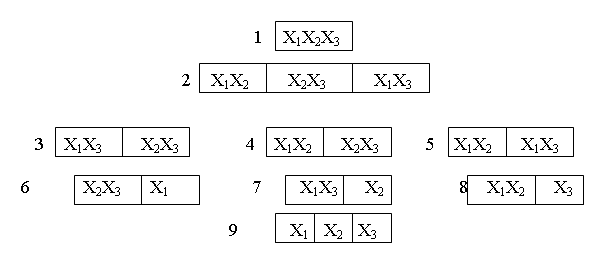
В этом множестве вариантов как видно не все удовлетворяют условиям структуризации (6,7,8,9).

Поэтому очевидно, что возникает вопрос, какой вариант структуризации наилучшим образом представляет заданную систему. Здесь возможны различные подходы. В самом общем виде условие выбора варианта можно сформулировать так. Лучшим вариантом структурированной системы является тот, который использует всю информацию исходной системы и не содержит ни какой другой.

Для систем, у которых определена функция поведения, это условие можно определить как принцип максимума нечетности. Конкретно для систем с вероятностной функцией поведение это принцип максимума энтропии т.е. лучший вариант структурированной системы обладает наибольшей величиной нечеткости или энтропии.

Однако в практических задачах нередко условие может потребовать минимизировать ошибку выбора варианта структуризации. Это условие можно сформулировать, как принцип минимального риска. В его основе лежит сравнение вариантов структуризации по близости функций поведения исходной и структуированной системы.

В ряде работ оценку близости функций поведения двух систем предлагается производить на основе класс метрических расстояний Минковского

d (f₁, f₂) = ∑ [f₁(d_k) - f₂(d_k)]^1/p

Функция ограничения полного множества состояний структурированной системы.

Пусть для исходной системы S = (X, T, C, Z) сформирована структурированная система S' = [(X¹, X²,..., Xm), T, Z], где Xⁱ ⊂ X. Каждую подсистему заданную на подмножестве αⁱ можно рассматривать как вариант упрощения исходной путем исключения переменных. Тогда если исходная система имеет функцию ограничения f, то подсистема будет иметь функцию ограничения вида

fⁱ = Пр_Xⁱ f

Это соотношение можно конкретизировать исходная система S имеет полное множество состояний С = (Ck, k=1,k), а каждая подсистема Sⁱ структуированной системы Cⁱ М C, тогда для значений fⁱ и f

f'(CX) = f(Ck)

Пример. Дана система S' с переменными a₁, a₂, a₃ и функцией поведения f_n.Найти функции поведения подсистем S₁ и S₂ c переменными соответственно a₁, a₂ и a₂, a₃.

dk a1 a2 a3 fn(dk)	d'k a1 a2 f'       fn(1)+fn(2)=       fn(3)+fn(4)=       fn(5)+fn(6)=       fn(7)+fn(8)
d''k a2 a3 f''       fn(1)+fn(5)=       fn(2)+fn(6)=       fn(3)+fn(7)=       fn(4)+fn(8)=

Пример. Даны три системы S₁, S₂, S₃ с переменными (a₁, a₂), (a₂, a₃), (a₁,a₃) с функциями поведения f_n', f_n'', f_n'''. Найти функцию поведения f_n системы S с переменными (a₁ a₂ a₃).

Из уравнения f^X(d) = ∑ f(d) следует система уравнений

d' a1 a2 fn'       0,4       0,3       0,2       0,1	d'' a2 a3 fn''       0,4       0,2       0,1       0,3	d''' a1 a3 fn'''       0,4       0,3       0,1       0,2
1. fn'(1) = fn(1) + fn(2) 2. fn'(2) = fn(3) + fn(4) 3. fn'(3) = fn(5) + fn(6) 4. fn'(4) = fn(7) + fn(8)	5. fn''(1) = fn(1) + fn(5) 6. fn''(2) = 7. fn''(3) = 8. fn''(4) =	9. fn'''(1) = 10. fn'''(2) = 11. fn'''(3) = 12. fn'''(4) =

Подставим в систему уравнений исходные данные для f^X(d) и учитывая ограничения

0 ≤ f_n(d) ≤ 1

Получим решение в виде неравенства

0,3 ≤ f_n(1) ≤ 0,4

Пример. Этот пример содержит описание исследования политической ситуации и уровня цен на бирже США.

• a₁ — политическая партия президента. Демократическая-0. Республиканская-1.
• a₂ — Большинство в палате представителей. Демократическая-0. Республиканская-1.
• a₃ — Большинство в сенате. Демократическая-0. Республиканская-1.
• a₄ — Уровень цен на бирже. Падает-0. Растет-1

Данные наблюдения регистрировались в период 1897—1921г. каждые 4 года т.е. в 21 интервале. Результаты наблюдения приведены в таблице.

Поскольку имеется 21 наблюдение и 16 состояний системы, т.о. ограничение на множество состояний задается в виде функций распределения возможностей

d1	a1	a2	a3	a4	N(dk)	f(dk)=N(dk)/maxn(dk)
						1,0
						0,33
						0,66
						0,165
						0,165
						0,165
						1,0

Варианты структурированных систем приведены в таблице в порядке возрастания меры расстояния δ = ∑ (f(d_k)-f_C(d_k))^1/p, где f_C(d_k) функции поведения структурированной системы.

N		δ
	123/134, 123/13/124/14 124/13	0,00072
	123/13/124	0,01383
	123/124/3	0,02774
	124/3/23	0,03335
	12/3/23/24	0,05796
	1/3/23/24, 12/3/23/4	0,16677
	1/3/23/4	0,28058
	1/23/4	0,41389
	1/2/3/4	0,5610

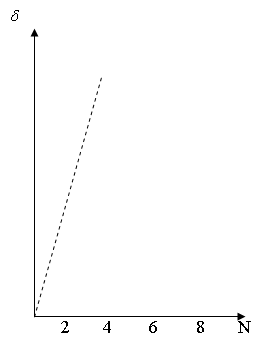
Интерпретация результатов решение задачи состоит в следующем. Из графика зависимости меры расстояния δ(f,f_C) от варианта структуризации видно, что он имеет характерную точку N=5. Структуированная система для варианта N=5 приведена ниже.

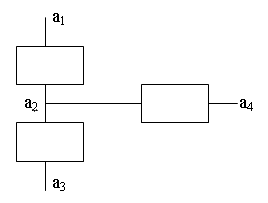
Из рисунка видно переменная a₂ является связующим звеном системы т.е. фактором определяющим цены на бирже в наибольшей степени.