Переменные, относящиеся к порядковой шкале или переменные, относящиеся к интервальной шкале, но не подчиняющиеся нормальному распределению

Количество сравниваемых выборок	Зависимость	Гест
	Независимые	U-тест Манна и Уитни
	Зависимые	тест Уилкоксона
>2	Независимые	Н-тест Крускала и Уоллиса
>2	Зависимые	тест Фридмана

Для каждой из этих двух групп тестов в SPSS имеются отдельные пункты меню, а именно Analyze (Анализ) Compare Means (Сравнение средних) или Analyze (Анализ) Nonparametric Tests (Непараметрические тесты)

Исключение составляет простой дисперсионный анализ с повторными измерениями. Этот метод нельзя найти в разделе Compare Means. Он вызывается командой меню General Linear Model (Общая линейная модель).

18. Дисперсионный анализ

Дисперсионный анализ – анализ влияния качественных факторов на количественные (Пр.: влияет ли качество – уровень обслуживания на посещаемость – обращение клиентов в банк).

Результат анализа – да/нет. Т.е. влияет качественный фактор или нет.

Проверяется нулевая гипотеза: Н0: сигма1 в квадрате=сигма2 в квадрате = сигма житое в квадрате = 0!!! Если применяется эта гипотеза, то качественный фактор НЕ оказывает влияние на количественный.

Н1: сигма1 в квадрате ≠сигма2 в квадрате ≠сигма житое в квадрате ≠ 0. Значит качественный фактор оказывает влияние на количественный.

Диперсионный анализ (МОДЕЛЬ):

Фактор – качество, либо свойство, в соответствии с которым классифицируется данные. Каждый фактор имеет несколько уровней (высокий, низкий уровень обслуживания)

Уровень – общий термин, используемый для описания конкретного свойства, определяющего каждую категорию рассматриваемой классификации.

Модель факторной системы:

Модель однофакторного анализа:Уij = M + τj + ξij

Уij – значение наблюдаемое. i – номер наблюдения, j – номер класса.

M – общая средняя по выборке

τj – эффект столбца

Если не будет влияния качественного фактора, то: Уij = M + ξij

Модель двуфакторная: оценивает влияет или нет два качественных фактора. Пр.: оценить влияет ли образование (гуманит, технич,..) и опыт работы (с….; без… - это уровни фактора) на уровень зарплаты.

Уij = M +αi + βj + ξij

Yij – наблюдаемое значение.

M – средний уровень (Хср зарплаты, например)

αi – влияние iго фактора

βj – jго фактора

ξij – случайная составляющая

Модель двуфакторная с взаимодействием факторов: Уij = M +αi + βj + ϒij + ξij

ϒij – совместное влияние iго и jго фактора.

Ограничения: - мат ожидание СВ равно 0. – остаточные СВ взаимно независимые E_ij. – все остаточные случайные величины имеют одинаковую дисперсию. – кажд св распределена по нормальному закону распределения.

В SPSS дисперсионный анализ выполняется так: Выберите в меню Analyze (Анализ) General Linear Model (Общаялинейнаямодель) Univariate... (Одномерная) Откроется диалоговое окно Univariate (Одномерная), Далее выбираются зависимые и независимые переменные и т.д.

Оценка значимости уравнения регрессии в целом дается с по­мощью F-критерия Фишера. При этом выдвигается нулевая ги­потеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у. Непосредственному расчету F-критерия предшествует анализ дисперсии.

Центральное место в нем занимает разложе­ние общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:

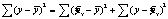
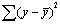- общая сумма квадратов отклонений

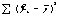- сумма квадратов

отклонения объясненная регрессией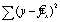

- остаточная сумма квадратов отклонения.

Статистическая гипотеза – это предположение о распределении

вероятностей, которое мы хотим проверить по имеющимся данным. Статистические гипотезы подразделяются на нулевые и альтернативные. ″Статистический критерий – это решающее правило, обеспечивающее надежное поведение, то есть принятие истинной и отклонение ложной гипотезы с высокой вероятностью″ Будем придерживаться следующего правила отклонения гипотезы об отсутствии различий (Н0 – нулевая гипотеза) и принятии гипотезы о статистической достоверности различий (Н1 -альтернативная).

19. Критерий Фишера

F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия вычисляется по формул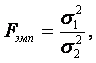е: где 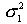- большая дисперсия, 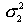- меньшая дисперсия рассматриваемых вариационных рядов. Если вычисленное значение критерия Fэмп больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Иными словами, проверяется гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H0={Dx=Dy}. Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости α и степеней свободы числителя (n1-1) и знаменателя (n2-1). Проиллюстрируем применение критерия Фишера на следующем примере. Дисперсия такого показателя, как стрессоустойчивость для учителей составила 6,17 (n1=32), а для менеджеров 4,41 (n2=33) (однородность – люди делятся по 1 признаку – профессия?). Определим, можно ли считать уровень дисперсий примерно одинаковым для данных выборок на уровне значимости 0,05 (0,05 - это вероятность, связанная с F-распределением, станд). Для ответа на поставленный вопрос определим эмпирическое значение критерия: 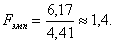При этом критическое значение критерия Fкр(0,05;31;32)=2. Таким образом, Fэмп=1,4<2=Fкр, поэтому нулевая гипотеза о равенстве генеральных дисперсий на уровне значимости 0,05 принимается. Fрасч>Fтабл, то принимается Н1. Если Fрасч<Fтабл, то принимается Н0.Однородность=отсутсвие различий в выборках:

Нулева́я гипо́теза — гипотеза, которая проверяется на согласованность с имеющимися выборочными (эмпирическими) данными. Часто в качестве нулевой гипотезы выступают гипотезы об отсутствии взаимосвязи или корреляции между исследуемыми переменными, об отсутствии различий (однородности) в распределениях (параметрах распределений) двух и/или более выборках. В стандартном научном подходе проверки гипотез исследователь пытается показать несостоятельность нулевой гипотезы, несогласованность её с имеющимися опытными данными, то есть отвергнуть гипотезу. При этом подразумевается, что должна быть принята другая, альтернативная (конкурирующая), исключающая нулевую, гипотеза. Используется при статистической проверке.

Стандартная ошибка коэффициента регрессии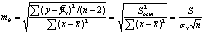

Для оценки существенности коэффициента регрессии его ве­личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: 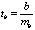которое затем сравнивается с табличным значением при определенном уровне значимости 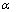и числе степеней свободы (n- 2).

Стандартная ошибка параметра а:

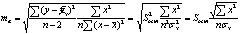
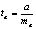
Значимость линейного коэффициента корреляции проверя­ется на основе величины ошибки коэффициента корреляции т_r:

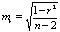
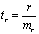
Общая дисперсия признака х: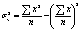

Коэф. регрессии 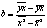Его величина показывает ср. изменение результата с изменением фактора на 1 ед.

Ошибка аппроксимации: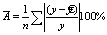

Проверка нулевой гипотезы

Признаки А и В будут независимыми, если значение, принятое признаком А не влияет на вероятности возможных значений признака В:

P (B_j / A_i) = P (B_i) или P (A_i, B_j) = P (A_i) P (B_j) (6.1)

Значения использованных вероятностей нам неизвестны, однако, по теореме Бернулли, при большом объеме выборки (n  ) частоты в ячейках таблицы сопряженности будут являться оценками этих вероятностей. При выполнении гипотезы о независимости признаков справедливо

p_ij = p_i.  p._j, (6.2)

где следующие величины трактуются как ожидаемые частоты:

,

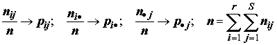(замена индекса точкой означает результат суммирования по этому индексу). Тогда проверка нулевой гипотезы сводится к оценке, насколько близки значения фактических и ожидаемых частот, т.е.

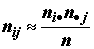. (6.3)

Методы сравнения эмпирических (H) и теоретических (T) частот по А. Брандту (А. Brandt) и Г. Снедекору (G.Snedecor) основываются на расчете критерия согласия  ², оценивающего меру близости по всем ячейкам таблицы сопряженности:

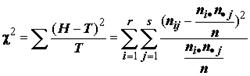. (6.4)

Если в конкретном опыте величина  ² оказывается чрезмерно большой, то приходится признать, что ожидаемые частоты слишком сильно отличаются от наблюдаемых. Ответ на естественный вопрос, о том, какие значения статистики следует считать чрезмерно большими, дает теорема К. Пирсона – Р. Фишера, из которой следует:

· для независимых признаков при неограниченном росте числа наблюдений распределение случайной величины  ² стремится к распределению “хи-квадрат”;

· гипотезу о независимости можно принять, если  ² не превосходит критического для заданного уровня табличного значения с (r –1)(s –1) степенями свободы;

· для зависимых признаков  ² неограниченно возрастает с увеличением n.

В 1934 г. Ф. Иэйтс (F.Yates) предложил ввести в выражение для статистики  ² так называемую поправку на непрерывность, которая связана с тем, что непрерывные распределения хи-квадрат и, соответственно, нормальное распределение используются для представления дискретных выборочных частот. С учетом такой поправки данное выражение примет следующий вид:

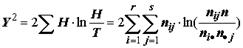. (6.5)