2015-05-05
2499
Если в пространстве V существует конечный набор векторов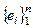 
такой что, ℒ 
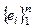º V, то система векторов 
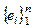называется полной системой в V, а пространство называется конечномерным. Таким образом, система векторов e 1, e 2, …, en Î V называется полной в V системой, т.е. если
" х Î V $ a1,a2, … a n ÎK такие, что x = a1 e 1 + a2 e 2 + … + a nen.
Если в пространстве V не существует конечной полной системы (а полная существует всегда – например, множество всех векторов пространства V), то пространство V называется бесконечномерным.
9°. Если 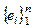полная в V система векторов и y Î V, то { e 1, e 2, …, en, y } – также полная система.
◀ Достаточно в линейных комбинациях коэффициент перед y брать равным 0. ▶
10°. Пусть { e 1, e 2, …, en } полный в V набор векторов, т.е. ℒ(e 1, e 2, …, en) º V и пусть $ a1,a2, … a n, такое, что en = a1 e 1 + a2 e 2 + … + a n –1 en –1. Тогда набор e 1, e 2 , …, en –1, тоже полный, т.е. ℒ(e 1, e 2 , …, en) º ℒ(e 1, e 2 , …, en –1) º V.
◀ { e 1, e 2, …, en } – полный Þ" х Î V $b1, b1, …, b n, что x = b1 e 1+ b2 e 2 +…+ b n en =
= b1 e 1 + b2 e 2 + … + b n –1 en –1 + b n (a1 e 1 + a2 e 2 + … + a n –1 en –1) =
|
|
|
= (b1 + b n a1) e 1 + (b2 + b n a2) e 2 + … + (b n –1 + b n a n –1) en –1 что и требовалось доказать. ▶
Используя, основанный на теореме 10°, процесс «прополки» (выбрасывание векторов, являющихся линейными комбинациями других векторов системы) можно построить минимальный полный набор векторов в пространстве V.
