Def: Оператор А, действующий в вещественном линейном пространстве называется линейным, если " x, y Î V, "aÎ R
1) A (x + y) = Ax + Ay
2) A (a x) = a A (x)
Def: Вектор x Î V, x ¹ 0 называется собственным вектором оператора А, если $aÎ R такое, что Ax = a x и a при этом называется собственным значением оператора А.
1°. Собственные значения оператора А являются корнями характеристического уравнения det(A – l Е) = 0. Наоборот, вообще говоря, неверно. Корень характеристического уравнения является собственным значением оператора А только в случае, когда этот корень вещественен.
Def: Оператор А * называется сопряженным к оператору А, если " х, y Î V, (Ax, y) = (x, A * y).
2°. Каждый линейный оператор А имеет единственный сопряженный оператор, который также является линейным.
При доказательстве этой теоремы в комплексном пространстве используется понятие полуторалинейной формы. В вещественном пространстве используется понятие билинейной формы.
Def: Функция В (x, y) называется билинейной формой в V, если " x, y Î V, "a, bÎ R:
1) B (a1 x 1 + a2 x 2, y) = a1 B (x 1, y) + a2 B (x 2, y)
2) B (x, b1 y + b2 y 2) = b1 B (x, y 1) + b2 B (x, y 2)
3°. Для любой билинейной формы В (x, y) существует линейный оператор А такой, что В (x, y) = (Ax, y).
Aналогом эрмитовых форм в вещественном пространстве служат симметричные билинейные формы.
Def: Билинейная форма В (x, y) называется симметричной, если B (x, y) = B (y, x). Билинейная форма В (x, y) называется кососимметричной, если B (x, y) = - B (y, x).
4°. Любую билинейную форму можно представить в виде суммы симметричной и кососиметричной билинейной формы.
5°. Для того, чтобы билинейная форма B (x, y), заданная в вещественном евклидовом пространстве V, была симметричной необходимо и достаточно, чтобы оператор А в представлении B (x, y) = (Ax, y) был самосопряженным.
Т°. Все корни характеристического многочлена самосопряженного линейного
оператора А в евклидовом пространстве – вещественны.
◀ Пусть l = a + b i – корень характеристического уравнения det(A – l E) = 0. Пусть (aik) – элементы матрицы оператора в некотором базисе { eik }, (aik Î R). Будем искать решение системы 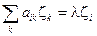 , где l = a + b i. Система имеет решение i =1, 2, 3, …, n, ибо определитель системы равен 0. Пусть решение
, где l = a + b i. Система имеет решение i =1, 2, 3, …, n, ибо определитель системы равен 0. Пусть решение 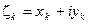 , k = 1, 2, 3, …, n. Подставляя в систему и приравнивая вещественные и мнимые части выражений, стоящих в левой и правой частях равенства, имеем:
, k = 1, 2, 3, …, n. Подставляя в систему и приравнивая вещественные и мнимые части выражений, стоящих в левой и правой частях равенства, имеем: 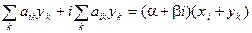 ,
,
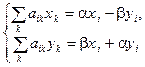 , или в векторном виде
, или в векторном виде 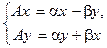 .
.
Умножим скалярно первое уравнение на y, а второе на x:
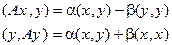 .
.
Учитывая, что (Ax, y) = (x, Ay) (ведь А – самосопряженный) имеем
a(x, y) – b(y, y) = a(x, y) + b(x, x), т.е. b((x, x) + (y, y)) = 0 Þ b = 0, т.е. l = aÎR ▶
6°. У каждого линейного самосопряженного оператора А в n – мерном евклидовом пространстве существует ортонормированный базис из собственных векторов.
7°. В базисе из нормированных ортогональных собственных векторов матрица линейного самосопряженного оператора А имеет диагональный вид и по диагонали стоят собственные значения.
8°. В произвольном ортонормированном базисе матрица самосопряженного оператора будет симметричной (АТ = А). Верно и обратное. Этим вещественный случай отличается от комплексного: в комплексном случае оператор А является эрмитовым, когда матрица этого оператора эрмитова (т.е. 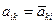 ).
).
 2015-05-05
2015-05-05 376
376








