Дипрогулка, дитропа, дипуть, дицикл

Дипрогулкой называется последовательность дуг, соединяющая две вершины. Каждая дуга в прогулке исходит из предыдущей вершины и заходит в последующую вершину ({v_i_-1, v_i} E). В дипрогулке вершины и дуги могут повторяться несколько раз.

Если наложить ограничения на повтор дуг или вершин, то получим:

Дитропа - дипрогулка, в которой запрещены повторы дуг;

дипуть- дитропа, в которой запрещены повторы вершин.

Замкнутая дипрогулка (дитропа, дипуть) начинается и заканчивается на одной и той же вершине.

Замкнутый дипуть называется дициклом (простым дициклом).

Каркасной дипрогулкой(дитропой, дипутем) называется дипрогулка (дитропа, дипуть), содержащая все вершины диграфа.

· k - длина дипрогулки(дитропы, дипути) диграфа - число дуг, составляющих дипрогулку (дитропу, дипуть) с учётом повторения.

· C^k – длина дицикла. Равна числу входящих в дицикл k дуг.

· g(D) – обхват диграфа. Является минимальной длиной дицикла, содержащегося в D.

· С(D) – окружность диграфа. Является максимальной длиной дицикла диграфа D.

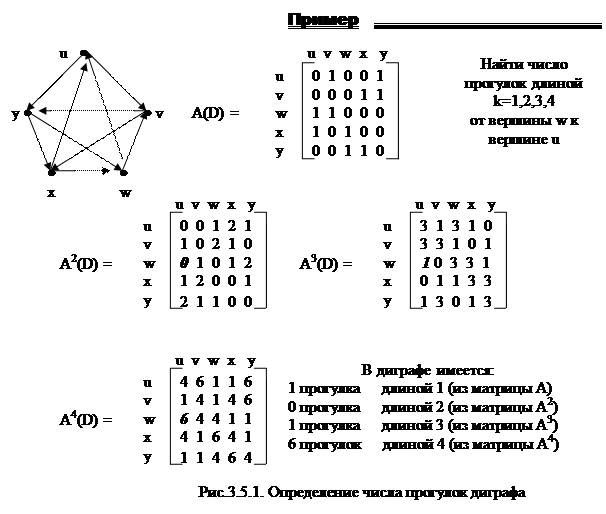
Число прогулок длиной r из вершины I в вершину j в диграфе D с n вершинами задаётся ij-ым элементом матрицы [A]^k,

где [A]- матрица связности диграфа,

[A]^k- k-ая степень этой матрицы.

Каждая дипрогулка содержит дипуть.

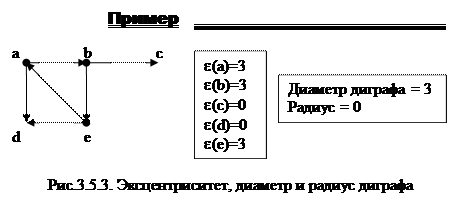
Эксцентриситет e(u) вершины u диграфа D=(V,A) определяется как максимальный из возможных всех путей от этой вершины до всех остальных вершин диграфа.

Эксцентриситеты вершин диграфа образуют вектор, максимальный элемент которого равен диаметру D диграфа, а минимальный – радиусу R направленного мультиграфа.

Вершины диграфа, эксцентриситет которых равен радиусу, образуют центр диграфа, а вершины с эксцентриситетом, равным диаметру, находятся на периферии диграфа.