МАТЕМАТИКА ДЛЯ ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ
Методические указания и контрольные задания для студентов-заочников
Якутск 2005
Утверждено научно-методическим советом университета
Научный редактор: д.т.н., профессор Ю.И.Трофимцев
Составитель
Г.П. Пермяков, доцент кафедры высшей математики ИМиИ ЯГУ
Методические указания составлены в соответствии с действующей программой по курсу «Математика» для студентов-заочников инженерно-технических специальностей. Они содержат перечень теоретических вопросов, литературу и 7 контрольных работ по следующим разделам: линейная и векторная алгебра, аналитическая геометрия, введение в математический анализ, дифференциальное и интегральное исчисление функции одной и нескольких переменных, ряды, дифференциальные уравнения, а также рекомендации по выполнению и оформлению контрольных работ.
Якутский государственный университет, 2005
Рекомендации по выполнению
И оформлению контрольных работ
Цель курса – научить студентов применению математики в специальных дисциплинах и изучении практических явлений.
|
|
|
Предназначено для студентов-заочников и содержит теоретические вопросы и контрольные задания. Каждое задание состоит из 20 вариантов. Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса по рекомендованным учебным пособиям.
Каждая контрольная работа должна быть выполнена в отдельной тетради, на обложке которой студенту следует написать свою фамилию, инициалы, адрес, шифр (номер зачетной книжки), название дисциплины и дату сдачи работы.
Решения необходимо приводить в той же последовательности, в какой даны условия задач. При этом условие задачи полностью переписывается перед её решением, в него вставляются необходимые данные.
В незачтенной работе студент должен исправить отмеченные ошибки и недочеты, учесть рекомендации и советы рецензента.
Студент должен выполнять контрольную работу по варианту, номер которого определяется следующим образом: а) если предпоследняя цифра в номере зачетной книжки четное число, то номер варианта совпадает с последней цифрой номера зачетной книжки; б) если предпоследняя цифра нечетная, то выбирается номер варианта с 11 по 20, последняя цифра которого совпадает с последней цифрой номера зачетной книжки.
Контрольная работа, выполненная с нарушением изложенных выше требований или выполненная студентом не по своему варианту, не зачитывается и возвращается без проверки.
Программа курса
I курс
Глава 1. Линейная и векторная алгебра ([1] Гл.: 9 п. 1-8, 10, гл.: 14 п.6 пп. 1, 2)
Векторы: определения, свойства, линейные операции над ними. Базис, размерность пространства. Разложения вектора по базису. Скалярное произведение векторов. Евклидово n-мерное пространство. Линейные нормированные пространства. Геометрическое изображение векторов в трехмерном пространстве. Координаты векторов, разложение вектора по прямоугольному базису. Нелинейные операции: скалярное, векторное, смешанное произведения векторов, свойства и применения произведений. Матрицы, операции над ними. Определители, их свойства. Обратная матрица. Системы линейных уравнений. Ранг матрицы, совместность систем уравнений. Отыскание решений линейной системы с помощью обратной матрицы. Правило Крамера, метод Гаусса.
|
|
|
Комплексные числа в алгебраической, тригонометрической и показательной формах. Геометрическое изображение комплексного числа. Модуль и аргумент комплексного числа. Операции над комплексными числами. Формула Муавра. Извлечение корня. Формулы Эйлера.
Глава 2. Аналитическая геометрия ([1] Гл.: 3, 9 пп. 9 – 14)
Прямоугольная декартовая система координат на плоскости и в пространстве. Простейшие задачи: расстояние между двумя точками, деление отрезка в данном отношении, площадь треугольника. Полярная система координат.
Линии и плоскости. Линии и поверхности в пространстве. Уравнения прямой на плоскости: общее, с угловым коэффициентом, через две точки, в «отрезках», нормальное. Кривые второго порядка на плоскости, их канонические уравнения. Плоскость и прямая в пространстве, различные виды их уравнений. Взаиморасположение прямой и плоскости в пространстве. Канонические уравнения поверхности второго порядка. Исследование формы поверхностей методом сечений.
Глава 3. Введение в математический анализ. Дифференциальное исчисление функции одной переменной ([1] Гл.: 1, 2, 4 – 6)
Множество действительных чисел. Модуль действительного числа. Погрешности вычисления. Функция.
Предел функции, свойства пределов. Первый замечательный предел. Последовательность, определение предела последовательности. Теорема Вейерштрасса о монотонной ограниченной последовательности. Размещения, сочетания, сочетания с повторениями. Бином Ньютона.
Число е. Второй замечательный предел. Бесконечно малые и бесконечно большие.
Сравнение бесконечно малых функций. Непрерывность функции. Арифметические действия над непрерывными функциями. Непрерывность
основных элементарных функций. Точки разрыва, их классификация. Свойства непрерывных функций. Равномерная непрерывность.
Производная функции. Приращение функции, определение производной, геометрическая и физическая интерпретации, правила дифференцирования. Производные элементарных функций. Таблица производных. Производные сложной и обратной функций. Дифференцируемость функции одной переменной. Связь между дифференцируемостью и непрерывностью, дифференцируемостью и существованием производных. Дифференциал функции одной переменной, его геометрический смысл. Инвариантность формы дифференциала. Производные и дифференциалы высших порядков. Физический и геометрический смысл второй производной. Производная функции, заданной с помощью параметра. Теоремы Ферма, Ролля, Лагранжа, Коши. Правило Лопиталя. Формула Тейлора для функции одной переменной.
Исследование и построение графиков функций. Возрастание и убывание функции на промежутки. Экстремумы. Наибольшее и наименьшее значения функции на отрезке. Выпуклость графика функции, точки перегиба. Асимптоты графика функции.
Глава 4. Интегральное исчисление функции одной переменной ([1] Гл.: 7, 8)
Неопределенный интеграл. Задача интегрирования, первообразная функция. Теорема о множестве первообразных. Неопределенный интеграл и его свойства, таблица интегралов. Методы интегрирования: непосредственное интегрирование, замена переменной и интегрирование по частям. Интегрирование некоторых классов функций. Разложение рациональных дробей на простейшие. Интегрирование простейших дробей и рациональных функций. Интегрирование иррациональных и тригонометрических функций. Дифференциальный бином.
|
|
|
Определенный интеграл как предел интегральных сумм. Суммы Дарбу и их свойства. Критерий интегрируемости. Свойства определенного интеграла. Оценки интеграла. Теорема о среднем.
Связь между определенным и неопределенным интегралами. Теорема Барроу о производной интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле. Интегрирование по частям. Приложения определенного интеграла к вычислению: а) Площади в декартовых и полярных координатах; б) Объема тела и поверхности вращения; в) Длины дуги кривой; г) Пути; д) Работы силы; е) Давления жидкости; ё) Количества электричества и т. д. Несобственные интегралы с бесконечными пределами и от неограниченных функций. Теоремы сравнения. Абсолютная и условная сходимость.
Курс
Глава 5. Дифференциальное и интегральное исчисление функции нескольких переменных ([1] Гл.: 12, 13)
Предел функции нескольких переменных. Непрерывность функции нескольких переменных. Частные приращения функции нескольких переменных, частные производные. Производные сложной и неявной функций.
Полное приращение функции. Полный дифференциал, его геометрическое истолкование. Частные производные высших порядков. Независимость смешанных производных от порядка дифференцирования. Дифференциалы высших порядков. Формула Тейлора для функции двух переменных. Экстремумы функции двух переменных. Необходимое условие экстремума, достаточные условия экстремума. Условный экстремум, метод множителей Лагранжа. Наибольшее и наименьшее значения функции.
Дифференциальная геометрия. Касательная и нормаль. Кривизна плоской кривой. Огибающая. Эволюта, эвольвента. Кривые в пространстве. Кривизна, кручение. Касательная, нормаль, бинормаль поверхности. Касательная плоскость.
|
|
|
Задачи, приводящие к понятиям кратных, криволинейных и поверхностных интегралов.
Двойной и тройной интегралы, их свойства. Вычисление кратных интегралов повторным интегрированием. Замена переменных в двойном и тройном интегралах. Площадь поверхности. Определение криволинейных интегралов первого и второго рода, их свойства, примеры вычисления. Определение поверхностных интегралов, их свойства, примеры вычисления. Интегралы, зависящие от параметра. Непрерывность, дифференцирование и интегрирование по параметру. Несобственные интегралы, зависящие от параметра. Гамма- и бета- функции.
Глава 6. Дифференциальные уравнения ([1] Гл.: 15)
Дифференциальные уравнения как модели основных законов природы. Определения дифференциального уравнения, его порядка, решения. Дифференциальные уравнения первого порядка. Задача Коши. Основные классы уравнений, интегрируемых в квадратурах. Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
Линейные дифференциальные уравнения. Свойства дифференциального оператора. Линейные однородные дифференциальные уравнения, свойства их решений. Линейно-независимые системы функций. Определитель Вронского. Фундаментальная система решений. Структура общего решения линейного однородного дифференциального уравнения. Линейные неоднородные дифференциальные уравнения, структура общего решения. Метод Лагранжа. Линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение для линейного однородного уравнения. Виды общего решения линейного однородного дифференциального уравнения в зависимости от корней характеристического уравнения. Метод неопределенных коэффициентов для решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами. Системы линейных дифференциальных уравнений в нормальной форме.
Глава 7. Теория рядов ([1] Гл. 14)
Числовые ряды. Сходимость и сумма ряда. Геометрическая прогрессия. Необходимое условие сходимости ряда. Действия над сходящимися рядами. Ряды с положительными членами. Теоремы сравнения. Признаки сходимости Даламбера, Коши. Интегральный признак сходимости. Знакочередующиеся ряды, признак Лейбница. Абсолютная и условная сходимость знакопеременных рядов. Свойства абсолютно сходящегося ряда.
Функциональные ряды, область сходимости, равномерная сходимость. Признак Вейерштрасса. Степенные ряды. Теорема Абеля, интервал и радиус сходимости. Равномерная сходимость степенных рядов. Интегрирование и дифференцирование. Ряд Тейлора. Единственность разложения функции в степенной ряд. Разложение функций в степенные ряды. Нормированные и гильбертовы пространства. Сходимость по норме. Полнота. Ортонормированные системы, полнота и замкнутость. Ряд Фурье. Равенство Парсеваля. Неравенство Бесселя. Тригонометрический ряд Фурье. Интеграл Фурье.
Контрольная работа 1. Линейная и векторная алгебра ([2] Гл. 4, 2)
Задача 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти её решение с помощью формул Крамера; 2) решить методом Гаусса; 3) записать систему в матричной форме и решить её средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение.
1. 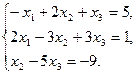 2.
2. 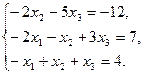
3. 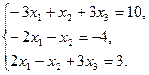 4.
4. 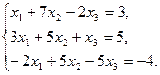
5. 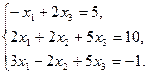 6.
6. 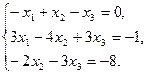
7. 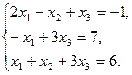 8.
8. 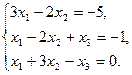
9. 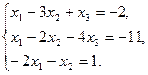 10.
10. 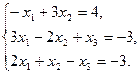
11. 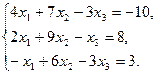 12.
12. 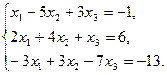
13. 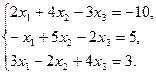 14.
14. 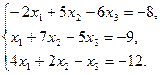
15. 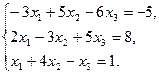 16.
16. 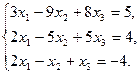
17. 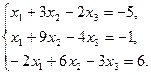 18.
18. 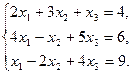
19. 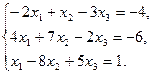 20.
20. 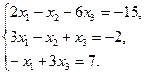
Задача 2. Коллинеарны ли векторы 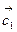 и
и 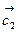 , построенные по векторам
, построенные по векторам 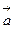 и
и 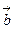 ?
?
1. 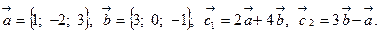
2. 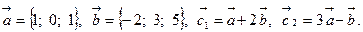
3. 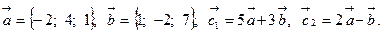
4. 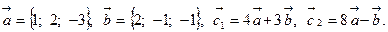
5. 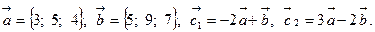
6. 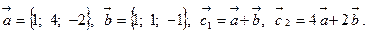
7. 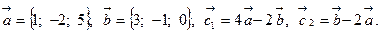
8. 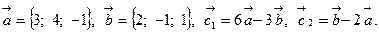
9. 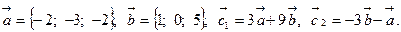
10. 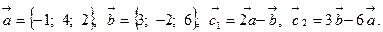
11. 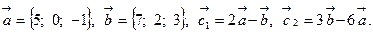
12. 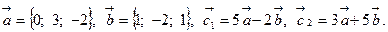
13. 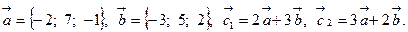
14. 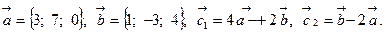
15. 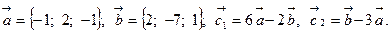
16. 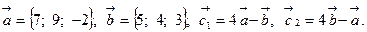
17. 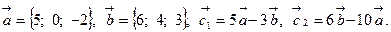
18. 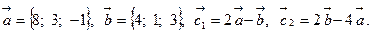
19. 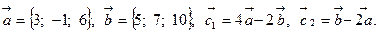
20. 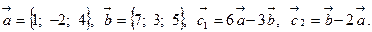
Задача 3. Найти косинус угла между векторами 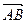 и
и 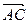 .
. 
1. 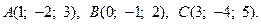 2.
2. 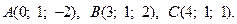
3. 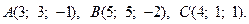 4.
4. 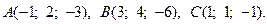
5. 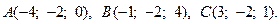 6.
6. 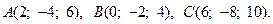
7. 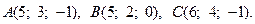 8.
8. 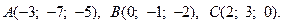
9. 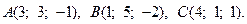 10.
10. 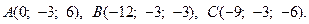
11. 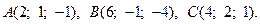 12.
12. 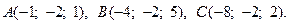
13. 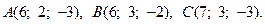 14.
14. 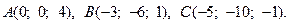
15. 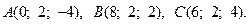 16.
16. 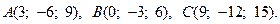
17. 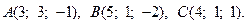 18.
18. 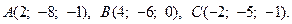
19. 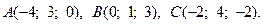 20.
20. 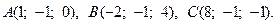
Задача 4. Вычислить площадь параллелограмма, построенного на векторах 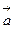 и
и 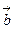 .
.
1. 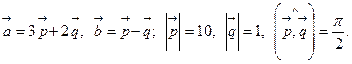
2. 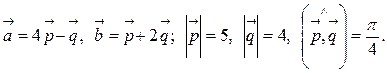
3. 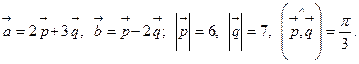
4. 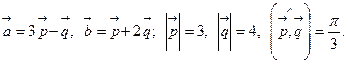
5. 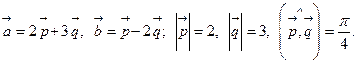
6. 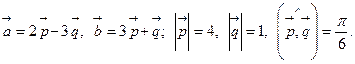
7. 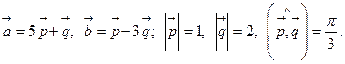
8. 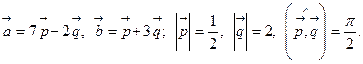
9. 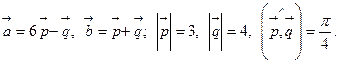
10. 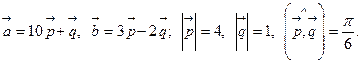
11. 
12. 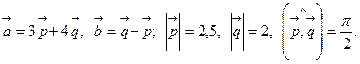
13. 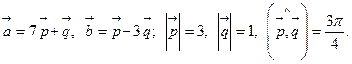
14. 
15. 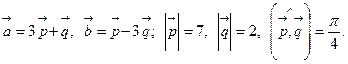
16. 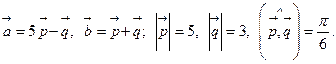
17. 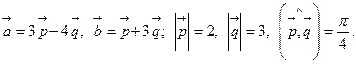
18. 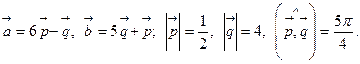
19. 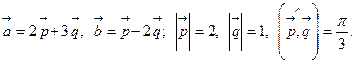
20. 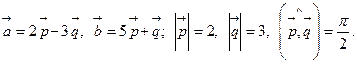
Задача 5. Написать разложение вектора 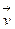 по векторам
по векторам 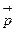 ,
, 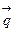 и
и 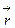 .
.
1. 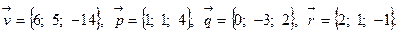
2. 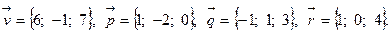
3. 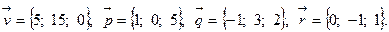
4. 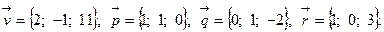
5. 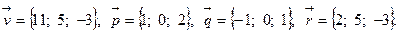
6. 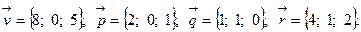
7. 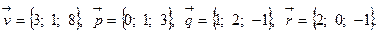
8. 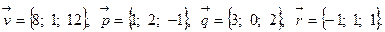
9. 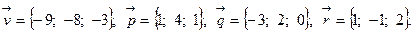
10. 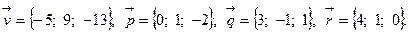
11. 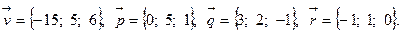
12. 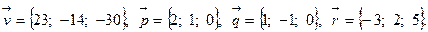
13. 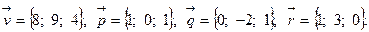
14. 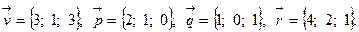
15. 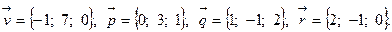
16. 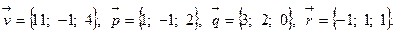
17. 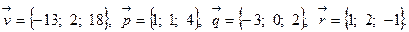
18. 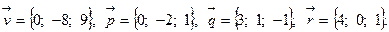
19. 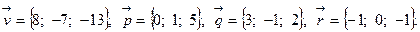
20. 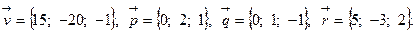
Задача 6. Определить собственные значения и собственные векторы матрицы третьего порядка.
1. 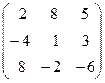 . 2.
. 2. 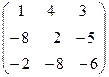 . 3.
. 3. 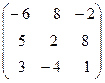 . 4.
. 4. 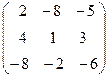 .
.
5. 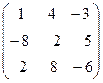 . 6.
. 6. 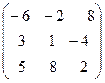 . 7.
. 7. 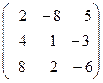 . 8.
. 8. 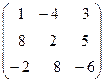 .
.
9. 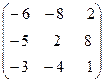 . 10.
. 10. 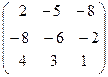 . 11.
. 11. 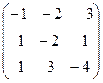 . 12.
. 12. 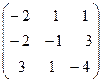 .
.
13. 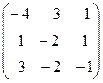 . 14.
. 14. 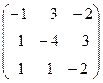 . 15.
. 15.  . 16.
. 16. 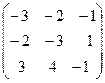 .
.
17. 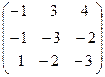 . 18.
. 18. 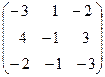 . 19.
. 19. 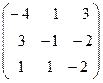 . 20.
. 20. 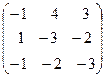 .
.
Контрольная работа 2. Аналитическая геометрия ([2] Гл. 1, 3)
Задача 1. Привести уравнение кривой второго порядка 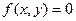 к каноническому виду и найти точки пересечения её с прямой:
к каноническому виду и найти точки пересечения её с прямой: 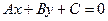 . Найти уравнение серединного перпендикуляра отрезка между точками пересечения, а также длину отрезка. Построить графики кривой, прямой и перпендикуляра.
. Найти уравнение серединного перпендикуляра отрезка между точками пересечения, а также длину отрезка. Построить графики кривой, прямой и перпендикуляра.
1. 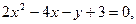
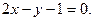 2.
2. 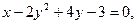
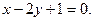
3. 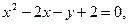
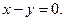 4.
4. 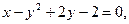
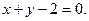
5. 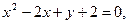
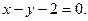 6.
6. 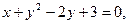
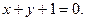
7. 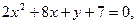
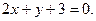 8.
8. 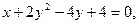
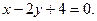
9. 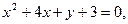
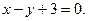 10.
10. 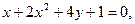
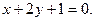
11. 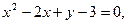
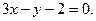 12.
12. 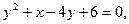
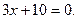
13. 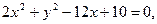
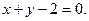 14.
14. 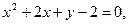
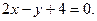
15. 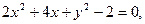
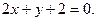 16.
16. 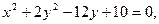
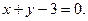
17. 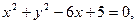
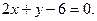 18.
18. 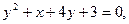
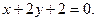
19. 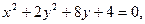
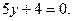 20.
20. 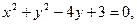
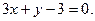
Задача 2. Необходимо: 1) построить по точкам график функции 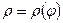 в полярной системе координат. Значения функции вычислить в точках
в полярной системе координат. Значения функции вычислить в точках 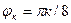 ; 2) найти уравнение кривой в прямоугольной декартовой системе координат, начало которой совмещено с полюсом, а положительная полуось
; 2) найти уравнение кривой в прямоугольной декартовой системе координат, начало которой совмещено с полюсом, а положительная полуось 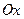 - с полярной осью; 3) определить вид кривой.
- с полярной осью; 3) определить вид кривой.
1. 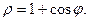 2.
2. 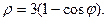 3.
3. 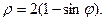 4.
4. 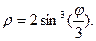
5. 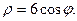 6.
6. 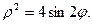 7.
7. 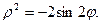 8.
8. 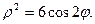
9. 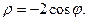 10.
10. 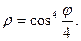 11.
11. 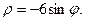 12.
12. 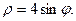
13. 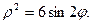 14.
14. 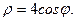 15.
15. 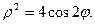 16.
16. 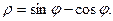
17. 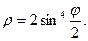 18.
18. 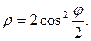 19.
19. 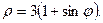 20.
20. 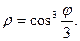
Задача 3. По координатам вершин пирамиды 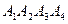 найти: 1) длину ребра
найти: 1) длину ребра 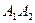 ; 2) угол между ребрами
; 2) угол между ребрами 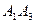 и
и 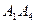 ; 3) угол между гранями
; 3) угол между гранями 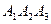 и
и 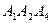 ; 4) уравнение прямой, проходящей через вершину
; 4) уравнение прямой, проходящей через вершину 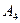 и центр тяжести грани
и центр тяжести грани 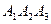 ; 5) длину и уравнение высоты из вершины
; 5) длину и уравнение высоты из вершины 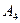 на грань
на грань 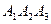 ; 6) расстояние между скрещивающимися ребрами
; 6) расстояние между скрещивающимися ребрами 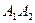 и
и 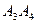 .
.
1. 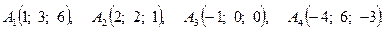
2. 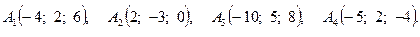
3. 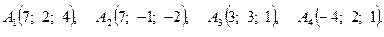
4. 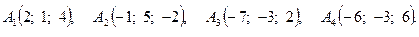
5. 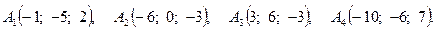
6. 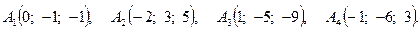
7. 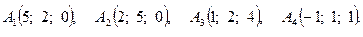
8. 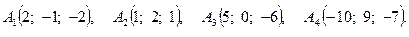
9. 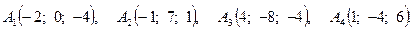
10. 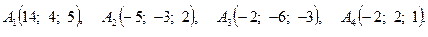
11. 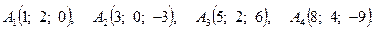
12. 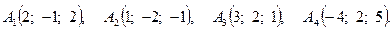
13. 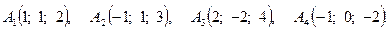
14. 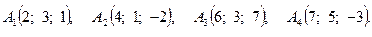
15. 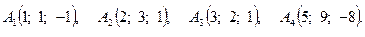
16. 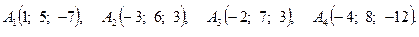
17. 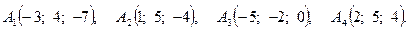
18. 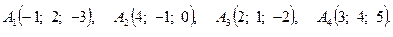
19. 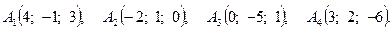
20. 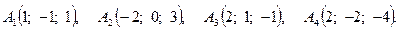
Задача 4. Написать канонические и параметрические уравнения заданной прямой, а также уравнение плоскости в «отрезках», перпендикулярной данной прямой и проходящей через точку 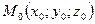 . Построить плоскость.
. Построить плоскость.
1. 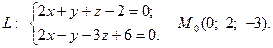 2.
2. 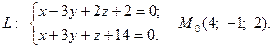
3. 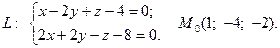 4.
4. 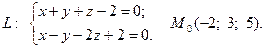
5. 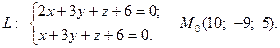 6.
6. 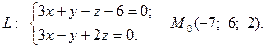
7. 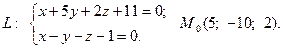 8.
8. 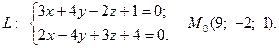
9. 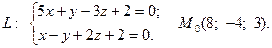 10.
10. 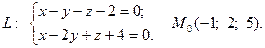
11. 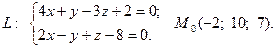 12.
12. 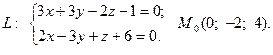
13. 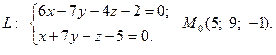 14.
14. 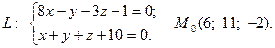
15. 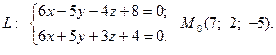 16.
16. 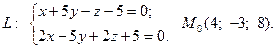
17. 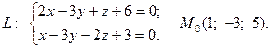 18.
18. 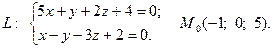
19. 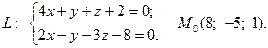 20.
20. 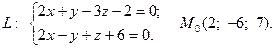
Задача 5. Найти точку пересечения прямой и плоскости, а также угол между ними.
1. 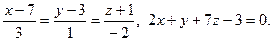 2.
2. 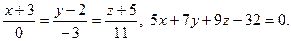
3. 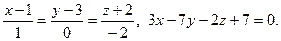 4.
4. 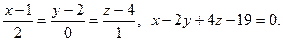
5. 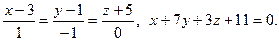 6.
6. 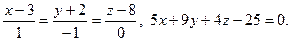
7. 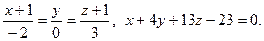 8.
8. 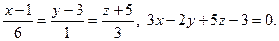
9. 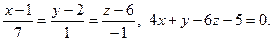 10.
10. 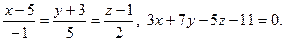
11. 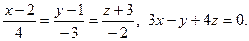 12.
12. 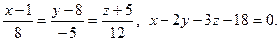
13. 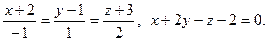 14.
14. 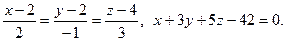
15. 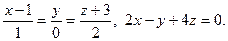 16.
16. 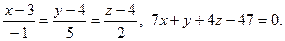
17. 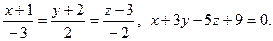 18.
18. 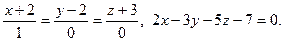
19. 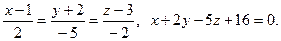 20.
20. 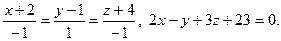
Контрольная работа 3. Введение в математический анализ.
Дифференциальное исчисление функции одной переменной ([2] Гл.6, 7)
Задача 1. Доказать, что:
1. 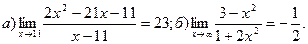 2.
2. 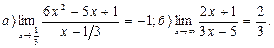
3. 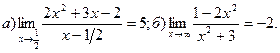 4.
4. 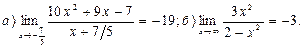
5. 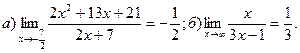 6.
6. 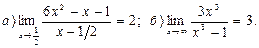
7. 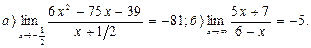 8.
8. 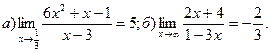
9. 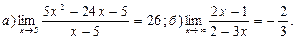 10.
10. 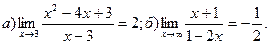
11. 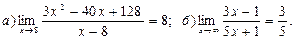 12.
12. 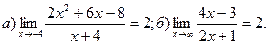
13. 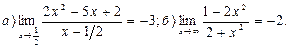 14.
14. 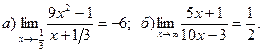
15. 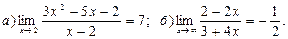 16.
16. 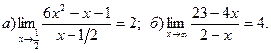
17. 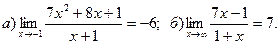 18.
18. 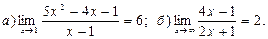
19. 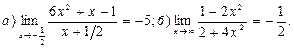 20.
20. 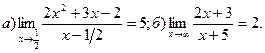
Задача 2. Вычислить пределы функций, не пользуясь правилом Лопиталя.
1. 
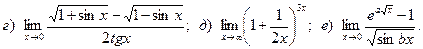
2. 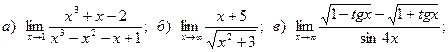
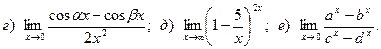
3. 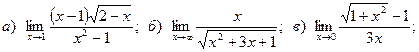
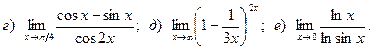
4. 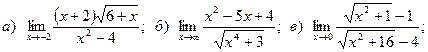
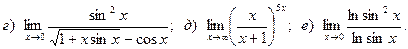
5. 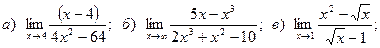
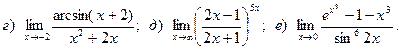
6. 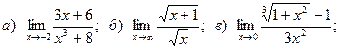
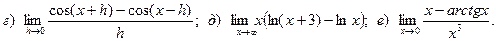
7. 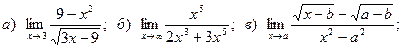
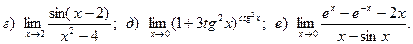
8. 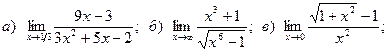
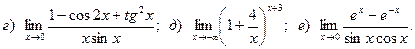
9. 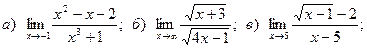
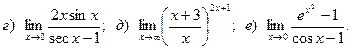
10. 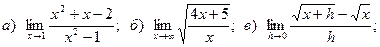
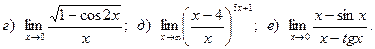
11. 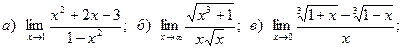
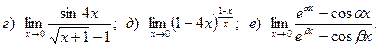
12. 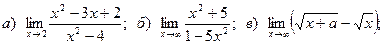
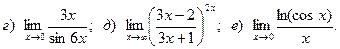
13. 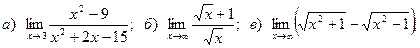
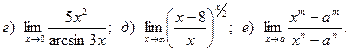
14. 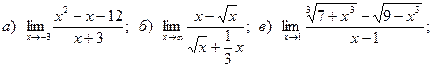
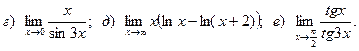
15. 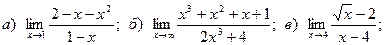
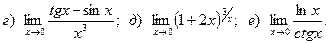
16. 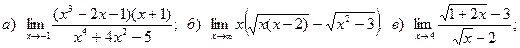
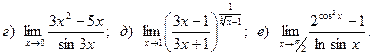
17. 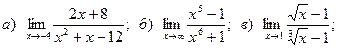
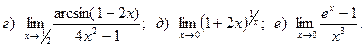
18. 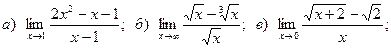
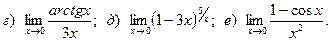
19. 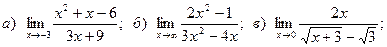
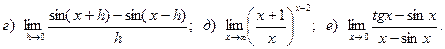
20. 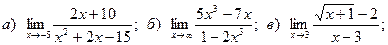
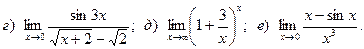
Задача 3. Доказать, что функция 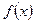 непрерывна в точке
непрерывна в точке 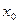 (найти
(найти 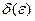 ) и, исходя из определения производной, найти производную
) и, исходя из определения производной, найти производную 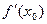 в точке
в точке 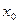 .
.
1. 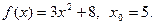 2.
2. 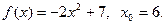 3.
3. 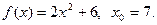
4. 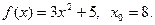 5.
5. 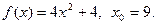 6.
6. 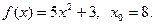
7. 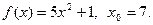 8.
8. 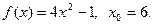 9.
9. 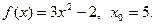
10. 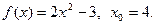 11.
11. 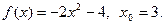 12.
12. 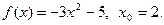
13. 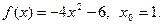 14.
14. 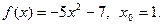 15.
15. 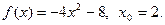
16. 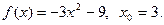 17.
17. 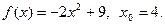 18.
18. 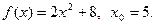
19. 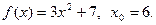 20.
20. 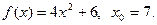
Задача 4. Найти производные функций.
1. 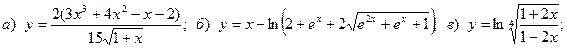
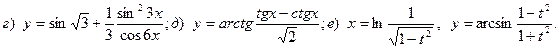
2. 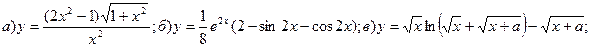
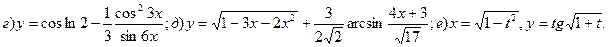
3. 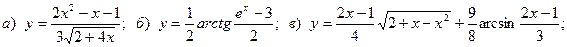
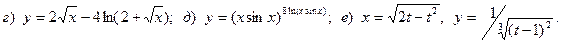
4. 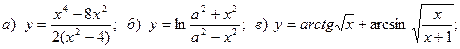
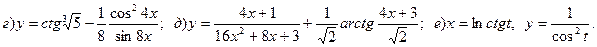
5. 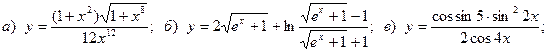
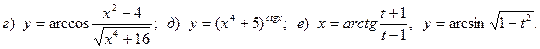
6. 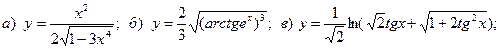
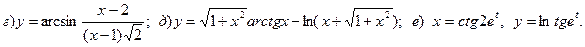
7. 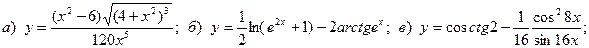
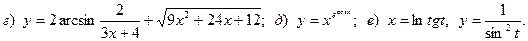
8. 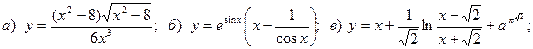
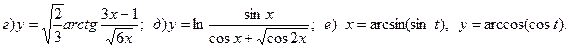
9. 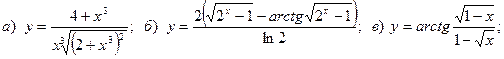
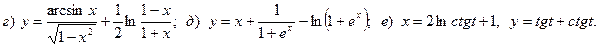
10. 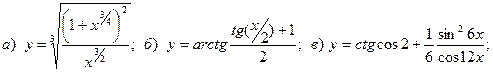
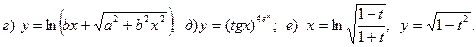
11. 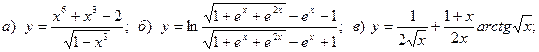
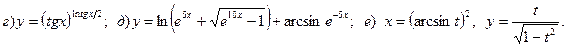
12. 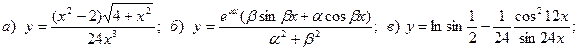
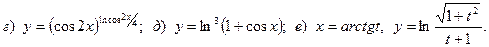
13. 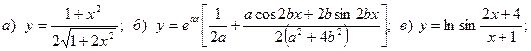
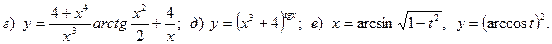
14. 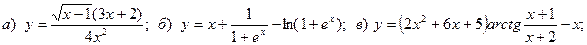
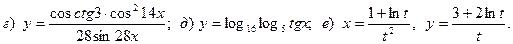
15. 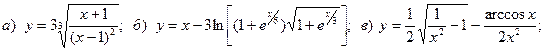
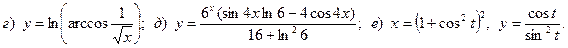
16. 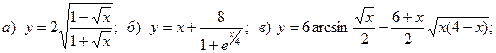
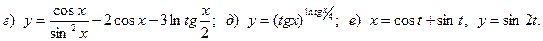
17. 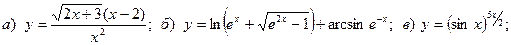
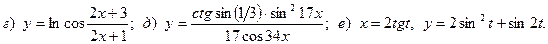
18. 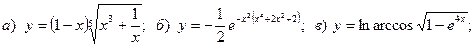
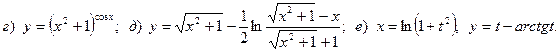
19. 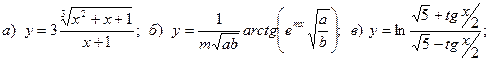
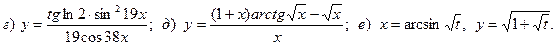
20. 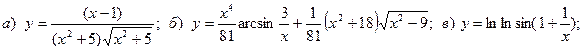
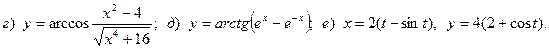
Задача 5. Провести полное исследование функций методами дифференциального исчисления и построить их графики.
1. 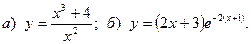 2.
2. 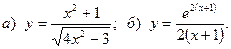
3. 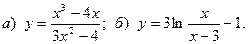 2.
2. 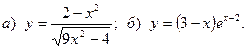
5. 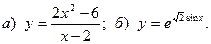 6.
6. 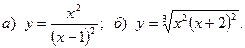
7. 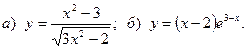 8.
8. 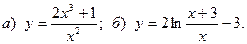
9. 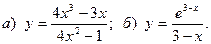 10.
10. 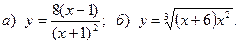
11. 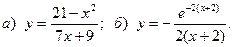 12.
12. 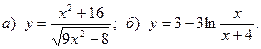
13. 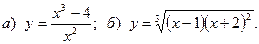 14.
14. 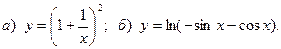
15. 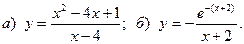 16.
16. 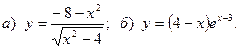
17. 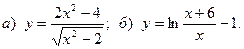 18.
18. 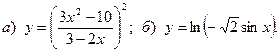
19. 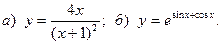 20.
20. 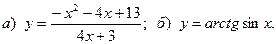
Задача 6 ([3] Гл. 3, п.7). а). Начертить в комплексной плоскости линии, точки которых удовлетворяют заданным уравнениям.
1. 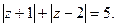 2.
2. 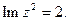 3.
3. 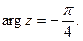 4.
4. 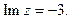
5. 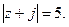 6.
6. 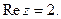 7.
7. 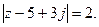 8.
8. 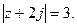
9. 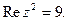 10.
10. 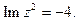
б). Определить, какие множества точек удовлетворяют заданным неравенствам.
11. 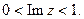 12.
12. 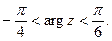 13.
13. 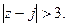 14.
14. 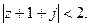
15. 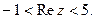 16.
16. 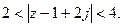 17.
17. 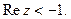 18.
18. 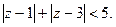
19. 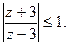 20.
20. 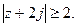
Контрольная работа 4. Неопределенный и определенный интегралы
([2] Гл. 9, 10)
Задача 1. Найти неопределенный интеграл.
1. 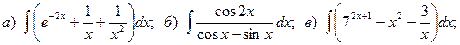
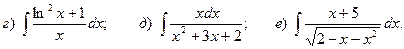
2. 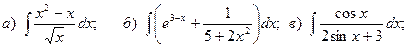
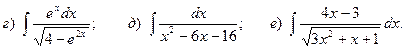
3. 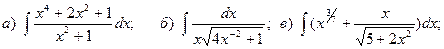
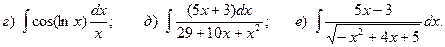
4. 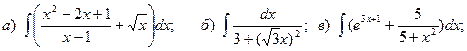
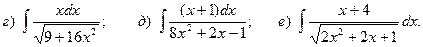
5. 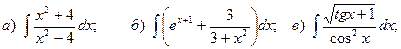
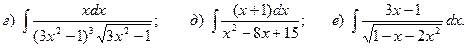
6. 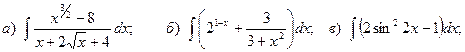
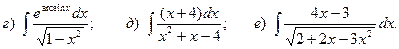
7. 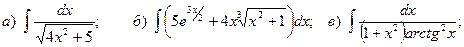
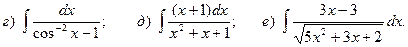
8. 
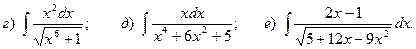
9. 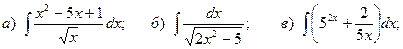
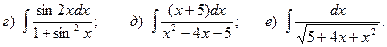
10. 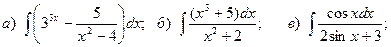
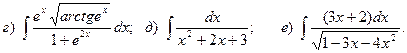
11. 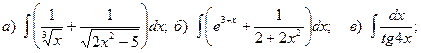
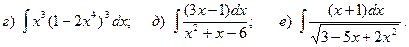
12. 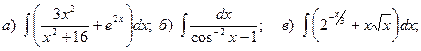
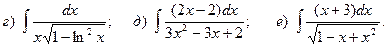
13. 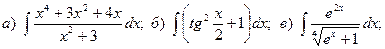
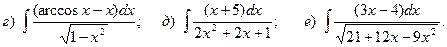
14. 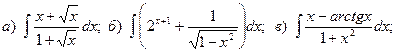

15. 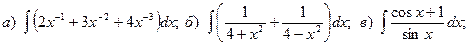
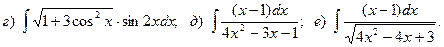
16. 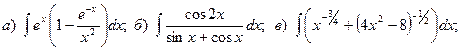
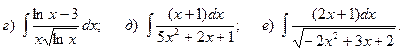
17. 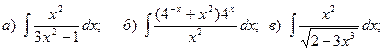
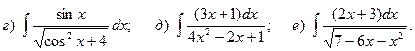
18. 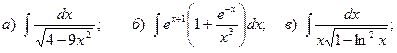
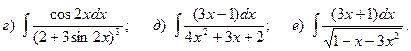
19. 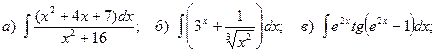
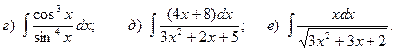
20. 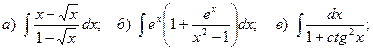
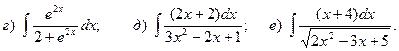
Задача 2. Найти неопределенный интеграл.
1. 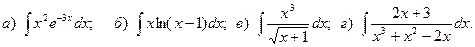
2. 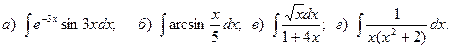
3. 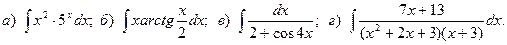
4. 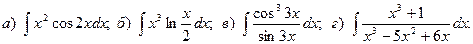
5. 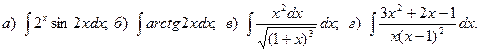
6. 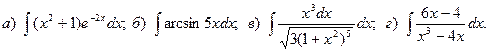
7. 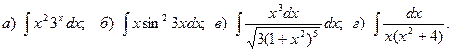
8. 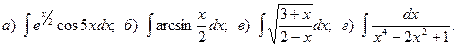
9. 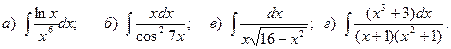
10. 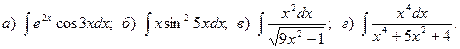
11. 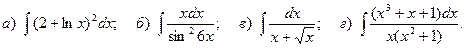
12. 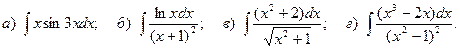
13. 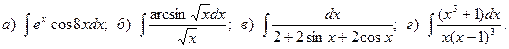
14. 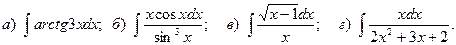
15. 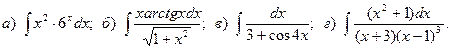
16. 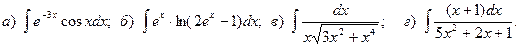
17. 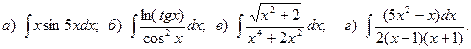
18. 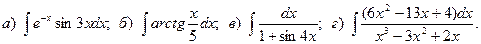
19. 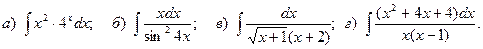
20. 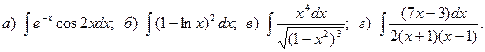
Задача 3. Нарисовать область, ограниченную данными линиями, и вычислить её площадь.
1. 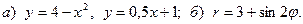 2.
2. 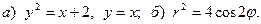
3. 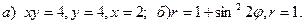 4.
4. 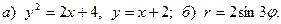
5. 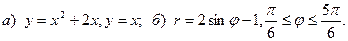 6.
6. 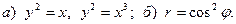
7. 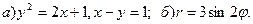 8.
8. 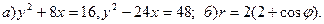
9. 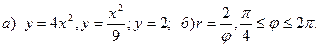 10.
10. 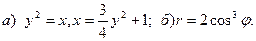
11 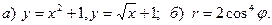 12.
12. 
13. 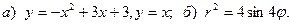 14.
14. 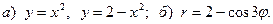
15. 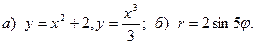 16.
16. 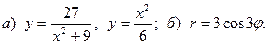
17. 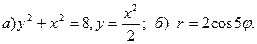 18.
18. 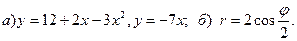 19.
19. 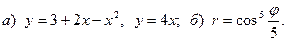 20.
20. 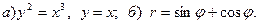
Задача 4. Вычислить объёмы тел, образованных вращением фигуры, (вокруг осей 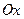 ,
, 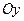 ), ограниченной заданными линиями.
), ограниченной заданными линиями.
1. 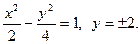 2.
2. 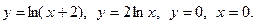
3. 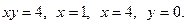 4.
4. 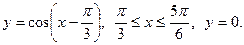
5. 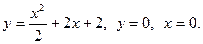 6.
6. 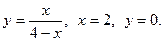
7. 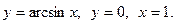 8.
8. 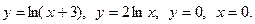
9. 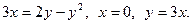 10.
10. 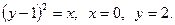
11. 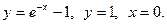 12.
12. 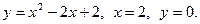
13.
 2015-05-06
2015-05-06 286
286






