Уравнения Колмогорова. Предельные вероятности состояние

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем на примере случайного процесса из, в котором мы изобразили граф. Будем полагать, что все переходы системы из состояния S_i в S_j происходят под воздействием простейших потоков событий с интенсивностями l_ij (i, j =0, 1, 2, 3); так, переход системы из состояния S ₀ в S ₁ будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния S ₁ в S ₀ — под воздействием потока «окончаний ремонтов» первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис.). Рассматриваемая система S имеет четыре возможных состояния: S ₀, S ₁, S ₂, S ₃.

Вероятностьюi - го состояния называется вероятность p_i (t) того, что в момент t система будет находиться в состоянии S_i. Очевидно, что для любого момента t сумма вероятностей всех состояний равна единице:

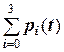=1. (8)

Рассмотрим систему в момент t и, задав малый промежуток D t,:найдём вероятность р ₀(t +D t) того, что система в момент t +D t будет находиться в состоянии S ₀. Это достигается разными способами.

1. Система в момент t с вероятностью р ₀(t) находилась в состоянии S ₀, а за время D t не вышла из него.

Вывести систему из этого состояния (см. граф на рис.) можно суммарным простейшим потоком с интенсивностью (l ₀₁+ l ₀₂), то есть в соответствии с (7), с вероятностью, приближенно равной (l ₀₁+ l ₀₂)D t. А вероятность того, что система не выйдет из состояния S ₀, равна [1-(l ₀₁+ l ₀₂)D t ]. Вероятность того, что система будет находиться в состоянии S ₀ по первому способу (т.е. того, что находилась в состоянии S ₀ и не выйдет из него за время D t), равна по теореме умножения вероятностей: р ₀(t)[1-(l ₀₁+ l ₀₂)D t ].

2. Система в момент t с вероятностями р ₁(t) (или р ₂(t)) находилась в состоянии S ₁ или S ₂ и за время D t перешла в состояние S ₀.

Потоком интенсивностью l ₁₀ (или l ₂₀ — см. рис.) система перейдет в состояние S ₀ с вероятностью, приближенно равной l ₁₀D t (или l ₁₀D t). Вероятность того, что система будет находиться в состоянии S ₀ по этому способу, равна р ₁(t) l ₁₀D t (или р ₂(t) l ₂₀D t).

Применяя теорему сложения вероятностей, получим

р ₀(t +D t)= р ₁(t) l ₁₀D t + р ₂(t) l ₂₀D t + р ₀(t)[1-(l ₀₁+ l ₀₂)D t ],

откуда

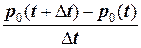= р ₁(t) l ₁₀+ р ₂(t) l ₂₀-(l ₀₁+ l ₀₂) р ₀(t),

Переходя к пределу при D t ®0 (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную 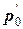(t) (обозначим ее для простоты ):

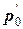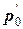= l ₁₀ р ₁+ l ₂₀ р ₂-(l ₀₁+ l ₀₂) р ₀,

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы S можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

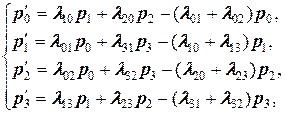(9)

Сформулируем правило составления уравнений Колмогорова: В левой части каждого из них стоит производная вероятности i - го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i - го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент t =0. Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии S ₀ т.е. при начальных условиях р ₀(0)=1, р ₁(0)= р ₂(0)= р ₃(0)=0.

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы р_i (t) в предельном стационарном режиме, т.е. при t ® 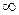, которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния S_i имеет четкий смысл: она называет среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния S ₀, т.е. р ₀=0,5, то это означает, что в среднем половину времени система находится в состоянии р ₀.

Так как предельные вероятности постоянны, то, заменяя в нениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы S с графом состояния, изображенном выше, такая система уравнений имеет

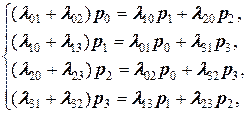(10)

Пример 2. Найти предельные вероятности для системы S из примера 1, граф состояний которой приведен на рис. выше, при l ₀₁=1, l ₀₂=2, l ₁₀=2, l ₁₃=2, l ₂₀=3, l ₂₃=1, l ₃₁=3, l ₃₂=2.

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

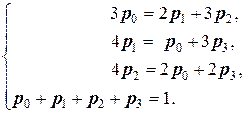(11)

(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим р ₀=0,40, р ₁=0,20, р ₂=0,27, р ₃=0,13, т.е. в предельном, стационарном режиме система S в среднем 40% времени будет находиться в состоянии S ₀ (оба узла исправны), 20% — в состоянии S ₁ (первый узел ремонтируется, второй работает), 27% — в состоянии S ₂ (второй узел ремонтируется, первый работает) и 13% времени — в состоянии S ₃ (оба узла ремонтируются).