Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
· факторы, формирующие тенденцию ряда;
· факторы, формирующие циклические колебания ряда;
· случайные факторы.
При различных сочетаниях в изучаемом процессе или явлении этих факторов зависимость уровней ряда от времени может принимать различные формы. Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую долговременное совокупное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное влияние на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию.
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку деятельность ряда отраслей экономики и сельского хозяйства зависит от времени года. При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой временного ряда.
Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты.
Существуют две основные цели анализа временных рядов: определение природы ряда и прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана.
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача статистического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем чтобы использовать полученную информацию для прогнозирования будущих значений ряда.
Ана́лиз временны́х рядо́в — совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования.
Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
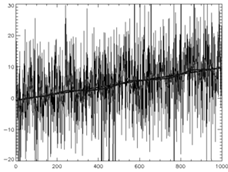
Пример временного ряда
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней:
- ряды абсолютных показателей;
- относительных показателей;
- средних величин.
- по количеству показателей, для которых определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды;
- временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины.
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Все модели временных рядов имеют общее свойство, которое основано на предположении значительной зависимости текущего значения уровня показателя yt от его предыстории. Иными словами уровень показателя yt генерируется значениями yt–1, yt–2,... на базе характерных для данного временного ряда закономерностях.
Указанное допущение выражается общим уравнением:
yt = f(yt-1, yt-2, …) + et (1.1)
где et – ошибка модели в момент t.
Здесь функция f отражает характер взаимосвязей, существующих в рассматриваемом временном ряду уt, t=1,2,... Удачный подбор функции f обусловливает высокую степень приближения правой «детерминированной» части выражения (1.1) к реальным значениям ряда. Степень этого приближения обычно характеризуется оценками и свойствами ошибки ряда et, t=1,2,... в данном случае имеется в виду, прежде всего минимальная дисперсия, соответствие белому шуму и т. п.
Для широкого круга процессов функция f имеет линейный вид. Например,
yt = а1yt-1 + аnyt-n + et.
Линейные модели временных рядов применяются, как правило, для описания стационарных процессов, при этом имеются в виду стационарные процессы второго порядка. У стационарного процесса n-го порядка значения всех своих моментов порядка n и ниже на всех временных отрезках, входящих в интервал t=1,2,..., Т отличаются постоянством. Строго стационарные процессы отличаются тем, что у них моменты всех порядков постоянны. Из сказанного следует, что для любых двух интервалов времени (Т1, Т2) и (Т3, Т4) для стационарного процесса второго порядка уt должны выполняться условия:
равенство математических ожиданий;
- равенство дисперсий;
- равенство однопорядковых коэффициентов автокорреляций.
Математически данные условия выражаются соотношениями:
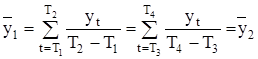 (1.2)
(1.2)
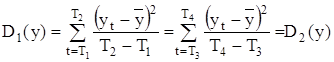 (1.3)
(1.3)
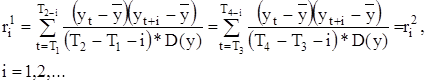 (1.4)
(1.4)
где 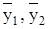 – оценки математических ожиданий;
– оценки математических ожиданий;
D1(y), D2(y) – оценки дисперсий;
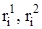 – оценки коэффициентов автокорреляции i-го порядка процесса уt на 1-ом и на 2-ом интервалах соответственно;
– оценки коэффициентов автокорреляции i-го порядка процесса уt на 1-ом и на 2-ом интервалах соответственно;
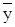 – среднее значение процесса (оценка математического ожидания) на интервале (1,Т);
– среднее значение процесса (оценка математического ожидания) на интервале (1,Т);
D(y) – оценка дисперсии процесса на интервале (1,Т).
При реальном изучении стационарных временных рядов равенства (1.2)–(1.4) рассматриваются в статистическом смысле. Это дает основания утверждать, что даже при неполном соответствии равенство 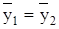 гипотеза о постоянстве математического ожидания процесса уt может быть принята в случае удовлетворения значений
гипотеза о постоянстве математического ожидания процесса уt может быть принята в случае удовлетворения значений 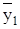 и
и 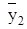 определенному статистическому критерию.
определенному статистическому критерию.
С целью проверки соответствия временного ряда уt, t=1,2,... стационарному процессу и выполнимости условий (1.2)–(1.4) применяются различные тесты. Если результаты одного из них не дают возможности утверждать об истинности или ложности выдвинутой гипотезы, то может возникнуть необходимость использовать несколько тестов для проверки одного и того же условия.
Всю совокупность тестов на стационарность временных рядов можно разделить на три основные группы: непараметрические, полупараметрические и параметрические тесты.
Непараметрические тесты не выдвигают заранее каких-либо сведений о законе распределения тестируемого временного ряда, его параметрах. Они основаны на изучении взаимосвязей между порядками следования образующих его значений, позволяют выявить наличие или отсутствие закономерностей в продолжительности и (или) чередовании их серий, образованных, например, последовательностями единиц совокупности с одинаковыми знаками, сменой знаков у этих единиц и т.п.
В полупараметрических тестах используются относительно слабые предположения о характере распределения значений временного ряда. Они отражают общие свойства функции распределения приростов значений ряда – симметричности, расположения квантилей.
При использовании методов этой группы оценки параметров распределения оцениваются по порядковым статистикам: среднее по медиане, среднеквадратическое отклонение – по размаху уровней ряда и т. п.
Параметрические тесты используют при относительно строгих предположениях о законе распределения временного ряда и его параметров. Данные тесты позволяют оценить степень приближенности эмпирических (наблюдаемых) характеристик распределения временного ряда к рассчитанным теоретическим уровням.
Именно эта степень приближенности позволяет принять или отвергнуть гипотезу о соответствии свойств рассматриваемого ряда стационарному процессу.
ПАРАМЕТРИЧЕСКИЕ ТЕСТЫ СТАЦИОНАРНОСТИ
При проверке гипотезы о постоянстве математического ожидания, интервал времени (1,Т) (и соответственно временной ряд уt, t=1,2,...Т) разбивается на две части, не обязательно одинаковые по количеству содержащихся в них значений уt, с количеством наблюдений Т1 (t=1,2,..., Т1) и Т2 (t=Т1+1,..., Т), Т2=Т–Т1.
Для каждой из частей определяются оценки 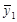 и
и 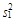 ,
, 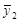 и
и 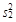 – выборочных математического ожидания и дисперсии переменной уt соответственно. Далее рассчитывается значение критерия Стьюдента по формуле:
– выборочных математического ожидания и дисперсии переменной уt соответственно. Далее рассчитывается значение критерия Стьюдента по формуле:
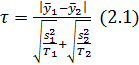
если предполагается, что значения дисперсий на этих участках не равны между собой, т. е. 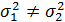 ,
,
и по формуле
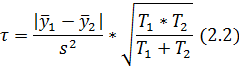
если 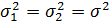
Если оказывается справедливым неравенство
t < t* (р* ,n), (2.3)
где р* – заданный уровень доверительной вероятности (р*=0,95; 0,97...); n=Т1+Т2–2 – число степеней свободы;
t*(р*,n) – критическое значение критерия Стьюдента, соответствующее значениям р* и n. то гипотезу о постоянстве математического ожидания процесса уt целесообразно принять. Вероятность ошибки такого решения при этом составляет 1–р*. В противном случае, т. е. при t>t*(р*,n), эта гипотеза отвергается.
Для большей достоверности вывода о постоянстве математического ожидания временного ряда уt, t=1,2,...,Т интервал наблюдений разделяется на несколько частей (если количество наблюдений достаточно велико). В этом случае проверяется гипотеза о равенстве оценок средних значений ряда, рассчитанных на этих частях. Для этих целей используется критерий Фишера. Его расчетное значение в тесте определяется как отношение взвешенной суммы квадратов отклонений этих оценок от средней временного ряда в целом к средней дисперсии временного ряда:
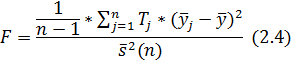
где n – число частей разбиения интервала (1,Т);
Тj – число измерений переменной уt на j-й части; j=1,2,..., n;
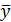 – среднее значение временного ряда в целом;
– среднее значение временного ряда в целом;
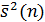 – средняя дисперсия, значение которой рассчитывается на основании следующей формулы:
– средняя дисперсия, значение которой рассчитывается на основании следующей формулы:
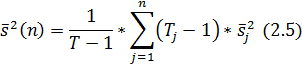
Где 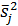 – дисперсия, рассчитанная на j-й части интервала (1,Т).
– дисперсия, рассчитанная на j-й части интервала (1,Т).
Если оказывается справедливым соотношение
F<F(р*,n1,n2), (2.6)
где F(р*,n1,n2) – табличное значение критерия Фишера для уровня доверительной вероятности p* и числе степеней свободы n1=n–1, n2=Т1+Т2+...+Тn–n то гипотеза о постоянстве математического ожидания временного ряда на всем интервале (1,Т) принимается с вероятностью р*. В противном случае она отвергается.
Тестирование дисперсии
Проверка гипотезы о постоянстве дисперсии временного ряда уt, t=1,2,...,Т в случае разбиения исходного интервала на две части осуществляется с использованием двухстороннего критерия Фишера. Обязательным условием при этом также является нормальный закон распределения значений уt .
Расчетное значение критерия Фишера определяется по следующей формуле:
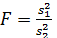 (2.7)
(2.7)
где 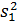 и
и 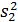 – оценки дисперсии ряда на первой и второй частях соответственно с числом измерений Т1 и Т2.
– оценки дисперсии ряда на первой и второй частях соответственно с числом измерений Т1 и Т2.
Если для заданного уровня доверительной вероятности р* оказывается, что значение F удовлетворяет неравенству
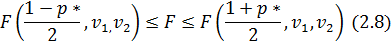
то гипотеза о постоянстве дисперсии временного ряда может быть принята, т. е. предположение о том, что 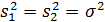 является обоснованным с вероятностью р*.
является обоснованным с вероятностью р*.
В выражении (2.8) значения 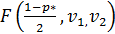 и
и 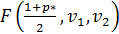 являются табличными (левосторонним и правосторонним) значениями критерия Фишера, соответствующими вероятности ошибки второго рода
являются табличными (левосторонним и правосторонним) значениями критерия Фишера, соответствующими вероятности ошибки второго рода 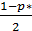 с числом степеней свободы
с числом степеней свободы 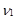 =Т1–1 и
=Т1–1 и 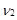 =Т2–1. Эти значения удовлетворяют следующему соотношению:
=Т2–1. Эти значения удовлетворяют следующему соотношению:
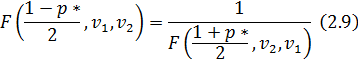
Вследствие этого обычно проверяется только соотношение:
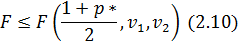
при условии, что 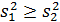 .
.
При средних (Т£100) и больших (Т>100) объемах временного ряда вместо критерия Фишера для проверки гипотезы о постоянстве его дисперсии используется стандартизованное нормальное распределение. В первом случае, т. е. при средних выборках, принимается во внимание, что закону N(0,1) подчиняется случайная величина, определяемая как
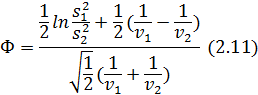
Во втором случае (при больших выборках) расчетное значение стандартизованной случайной величины оценивается следующим образом:
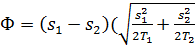 ) (2.12)
) (2.12)
В обоих случаях, если оказывается справедливым соотношение
|F|<F(р*), (2.13)
где F(р*) – табличное значение стандартизованного нормального закона, соответствующего доверительной вероятности р*то гипотеза о постоянстве дисперсии принимается.
При разбиении временного ряда уt, t=1,2,...,Т на несколько частей (п>2) для проверки гипотезы о постоянстве дисперсий используется критерий Кокрена, основанный на распределении Фишера. Он обычно применяется в предположении, что объемы этих частей равны между собой, т. е. Т1=Т2=... =Тп=N. Расчетное значение этого критерия определяется по следующей формуле:
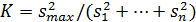 (2.14)
(2.14)
где 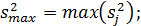
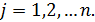
Табличное значение критерия Кокрена, соответствующее заданной доверительной вероятности и числам степеней свободы n1=п и n2=Т–1, определяется на основании табличного значения F-критерия следующим образом:
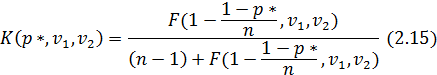
где p* – уровень доверительной вероятности, 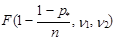 – табличное значение критерия Фишера, выбранное для уровня доверительной вероятности
– табличное значение критерия Фишера, выбранное для уровня доверительной вероятности 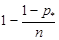 и числа степеней свободы n1=N–1 и n2=(п –1)×n1.
и числа степеней свободы n1=N–1 и n2=(п –1)×n1.
Если оказывается справедливым соотношение
К< К(p*, п,n1), (2.16)
то гипотеза о постоянстве дисперсии временного ряда уt, t=1,2,..., Т принимается с вероятностью p*.
Более мощным по сравнению с критерием Кокрена, но и одновременно более чувствительным по отношению к отклонениям от нормального вида закона распределения значений временного ряда уt, t=1,2,...,Т является критерий Бартлетта. Этот критерий обычно используется при проверке гипотезы о постоянстве дисперсии нормально распределенного ряда при разбиении на интервале (1,Т) на число частей, превышающее два.
Критерий Бартлетта основан на использовании распределения Пирсона – c2. Согласно этому критерию случайная величина l, рассчитанная на основе следующего выражения:
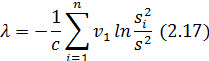
Где n – оценка дисперсии на i-м интервале;
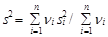 – средняя дисперсия на п интервалах;
– средняя дисперсия на п интервалах;
ni=Ti–1 – число степеней свободы на i-м интервале.
Величина с рассчитывается согласно следующей формулы:
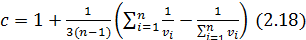
При больших значениях ni , с»1.
Для частного случая, когда n1=n2=...=nn=n и, таким образом, 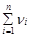 =T–n,
=T–n,
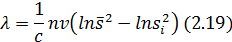
где с=1+[(n+1)/3k×n].
Если расчетное значение l не превышает табличного значения c2(p*,n), где p* – уровень доверительной вероятности и n=п–1 – число степеней свободы, то гипотеза о равенстве дисперсий s12 =s22=...=s2 на рассматриваемых частях временного интервала (1,Т), т. е. гипотеза о постоянстве дисперсии временного ряда уt, t=1,2,..., Т принимается. В противном случае, когда l³c 2 (p* , п –1), эта гипотеза отвергается.
2.3 Тестирование коэффициентов автокорреляции
Для проверки гипотезы о постоянстве коэффициентов автокорреляции используются те же процедуры (критерии), что и для проверки аналогичных гипотез для средних (автокорреляция) и дисперсии (автоковариация). К результатам такой проверки следует относиться с определенной осторожностью, особенно при использовании критерия Стьюдента. Это обусловлено тем, что дисперсии выборочных коэффициентов автокорреляции определяются с достаточно большой погрешностью, которая увеличивается с ростом значений самого коэффициента автокорреляции. Рост погрешности вызван, прежде всего, усиливающимися в этой ситуации несимметричностью закона распределения выборочного коэффициента автокорреляции и его расхождением с нормальным распределением. Увеличивает погрешность и возрастающая с увеличением значений выборочных коэффициентов автокорреляции ковариационная связь между ними. В частности, Бартлетт показал, что между парами выборочных коэффициентов автокорреляции существует достаточно сильная статистическая связь. Ее величина при больших задержках приблизительно может быть оценена на основании следующего выражения:
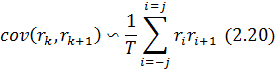
где ri – значений i-го выборочного коэффициента автокорреляции.
Наличие такой связи может вносить существенные смещения в оценки значений, как самих коэффициентов автокорреляции, так и в их дисперсии.
В общем случае, величина дисперсии коэффициента автокорреляции может быть оценена с использованием формулы Бартлетта:
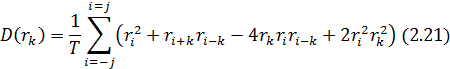
где индекс j зависит от длины ряда Т.
Его величина определяется требованием статистической достоверности используемых в выражении (2.21) значений коэффициентов автокорреляции, в первую очередь, значений 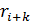 .
.
Для реальных временных рядов автокорреляционная функция часто имеет вполне определенный вид. Коэффициенты автокорреляции могут быть равны нулю после некоторой задержки, т. е. ri=0, i>k, затухать по экспоненте, rk=rik. В последнем случае, например, дисперсия первого коэффициента автокорреляции может быть определена приблизительно по следующей формуле:
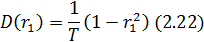
При небольших значениях коэффициента автокорреляции его распределение является приблизительно нормальным. Его дисперсия в этом случае может быть приблизительно оценена по следующей формуле:
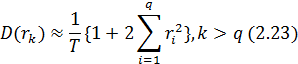
где индексы k принадлежат приближающимся к нулю коэффициентам автокорреляции после некоторой задержки q.
В практических расчетах используют упрощенную формулу дисперсии коэффициентов, имеющую следующий вид:
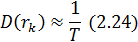
Выражения (2.23) и (2.24) могут быть применены при определении значимости (отличности от нуля) коэффициентов автокорреляции с использованием критерия Стьюдента. Его значение рассчитывается на основании следующей формулы:
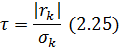
НЕПАРАМЕТРИЧЕСКИЕ ТЕСТЫ СТАЦИОНАРНОСТИ
Параметрические критерии проверки стационарности достаточно неудобны в практических исследованиях и весьма ограничены в применении из-за своих достаточно строгих предположений относительно нормальности закона распределения временного ряда уt, t=1,2,.... Они требуют значительных вычислений.
На практике при проверке свойств стационарности процессов часто используются непараметрические критерии, которые не имеют подобных ограничений по закону распределения временного ряда уt, да и не столь сложны по своим вычислениям.
Тест Манна-Уитни (тестирование математического ожидания)
Вместо критерия Стьюдента может быть использован непараметрический критерий Манна-Уитни (критерий и*). Он чуть слабее критерия Стьюдента в случае временных рядов с нормальным распределением, однако, имеет неоспоримые преимущества по сравнению с параметрическими критериями в случае, если распределение временного ряда отличается от нормального.
Критерий и* применяется для проверки идентичности распределений двух совокупностей (в нашем случае, временных последовательностей одного временного ряда уt, определенных на разных временных частях интервала t=1,..., Т).
Предположим, что первая совокупность образована Т1 последовательными значениями уt, а вторая – Т2 его последовательными значениями, и эти последовательности не пересекаются.
Все значения этих совокупностей объединяются в один ряд, в котором они располагаются в порядке возрастания с первого по (Т1+Т2)-й вне зависимости от принадлежности к той или иной последовательности. Вместе с тем, в этой единой последовательности символом у1 отмечаются элементы первой последовательности, а символом у2 – второй. В результате формируется структурный временной ряд, состоящий из Т1+Т2 элементов, в котором символы у1 (Т1 элементов) и символы у2 (Т2 элементов) оказываются перемешанными между собой.
Логика теста состоит в следующем. Если ряд стационарный, то последовательности у1 и у2 практически не отличаются одна от другой и их элементы перемешаны между собой. При этом появление каждой из возможных структур имеет равную вероятность. Если же ряд отличается от стационарного, то общая последовательность будет разделена на более или менее однородные массивы, состоящие в основном из единиц той или иной совокупности.
Тест Манна-Уитни осуществляет проверку гипотезы о стационарности временного ряда уt на основе расчета статистики и* (значения критерия), представляющей собой число случаев, когда элементы из совокупности у1 предшествуют элементам совокупности у2.
Значение и* рассчитывается либо через сумму рангов элементов первой совокупности, либо через сумму рангов элементов второй совокупности, с которыми оно связано следующими соотношениями:
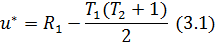
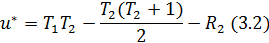
где R1 и R2 – суммы рангов элементов первой и второй совокупностей соответственно, определяемых по их общей последовательности.
Для больших последовательностей (Т>50; 100) случайная величина и* распределена по нормальному закону с математическим ожиданием
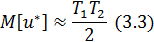
и дисперсией
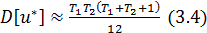
Таким образом, случайная величина z, определяемая как
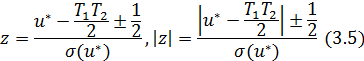
является нормированной величиной с нулевым средним и единичной дисперсией, распределенной по стандартизованному нормальному закону, z~N(0,1).
В формуле (3.5) поправка 1/2 вводится для обеспечения непрерывности величины z.
Она прибавляется, если z<0, и вычитается, при z>0.
Если обе совокупности идентичны, и их элементы будут перемешаны между собой, то можно ожидать, что значения и* будут находиться недалеко от своего среднего уровня (соответственно z – около нуля). Гипотеза о стационарности процесса уt, t=1,2,..., Т в этом случае может быть принята с доверительной вероятностью p*, если будет выполнено следующее неравенство:
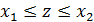 (3.6)
(3.6)
где х1 и х2 определяются из следующего равенства:
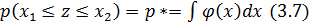
где 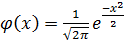
В частности, при p*=0,95, расчетное значение z должно находиться в следующем интервале: –1,96£ z£1,96.
Тест Сиджела-Тьюки
Вместо параметрического критерия Фишера (F-критерия) для проверки гипотезы о постоянстве дисперсии временного ряда уt на интервале t=1,2,...,Т используется непараметрический критерий Сиджела-Тьюки, который также основан на сопоставлении рангов элементов двух совокупностей из рассматриваемого интервала.
Исходный временной ряд уt, t=1,2,...,Т центрируется, т. е. определяются значения 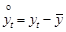 , где
, где 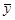 – среднее значение ряда уt. Далее интервал (1,Т) разделяется на две части (желательно равные), так что на первой из них располагаются элементы первой центрированной совокупности у1, а на второй – элементы второй совокупности – у2. Далее элементы из двух центрированных совокупностей у1 и у2 объединяются в одной таблице с запоминанием “своей совокупности” согласно следующему правилу ранжирования:
– среднее значение ряда уt. Далее интервал (1,Т) разделяется на две части (желательно равные), так что на первой из них располагаются элементы первой центрированной совокупности у1, а на второй – элементы второй совокупности – у2. Далее элементы из двух центрированных совокупностей у1 и у2 объединяются в одной таблице с запоминанием “своей совокупности” согласно следующему правилу ранжирования:
· Ранг 1 приписывается наименьшему отрицательному значению, которое располагается на первом месте вверху таблицы.
· Ранг 2 приписывается наибольшему положительному значению, которое располагается на последнем месте внизу таблицы.
· Ранг 3 приписывается значению, следующему за наименьшим, которое располагается на втором месте вверху таблицы.
· Ранг 4 – значению, следующему за наибольшим, которое располагается в таблице на втором месте снизу. Ранг 5 приписывается третьему по порядку наименьшему значению. Оно располагается в таблице на третьем месте сверху.
· Ранг 6 приписывается третьему по порядку наибольшему значению, которое располагается на третьем месте таблицы снизу и т. д.
Рассчитанная на основе этих рангов случайная величина w* оказывается приблизительно распределенной по нормальному закону с математическим ожиданием, оцениваемым как
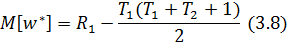
и дисперсией
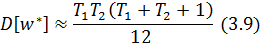
где R1 – сумма рангов элементов первой совокупности у1,
Т1+Т2 – количество элементов в первой и второй совокупности соответственно.
Из выражений (3.8) и (3.9) следует, что нормированная случайная величина z, определяемая как
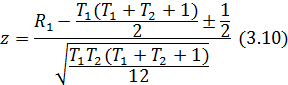
Гипотеза о равенстве дисперсий рассмотренных совокупностей принимается, если для z удовлетворяется соотношение (3.6).
Тест Вальда-Вольфовитца
Для проверки гипотезы о стационарном характере процесса (имеется в виду стационарность второго порядка) может быть использованы достаточно универсальные относительно закона распределения значений ряда уt, t=1,2,..., Т непараметрические тесты, основанные на анализе закономерностей серий этих значений (сериальные критерии). Необходимым условием их применения является достаточно большой объем временного ряда, что позволяет с определенной обоснованностью считать обнаруженные закономерности устойчивыми (характерными для данного ряда). При этом серией называют последовательность значений, предшествующая или следующая за некоторым значением, характерный признак которого отличается от признака элементов, входящих в серию. В качестве такого признака часто рассматривается расположение элемента последовательности относительно ее медианы. В этом случае серии с положительным знаком образуют элементы по уровню выше медианы, и серии с отрицательным знаком – элементы, чей уровень не превосходит медианы. Здесь следует иметь в виду, что один элемент – это тоже серия.
Примером сериального критерия является критерий Вальда-Вольфовитца, основанный на подсчете общего числа серий. Среднее значение числа серий определяется согласно следующему выражению:
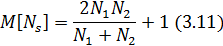
а его дисперсия – согласно формуле
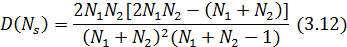
где N1 – количество элементов с положительным знаком;
N2 – количество элементов с отрицательным знаком;
N1+N2=Т – количество элементов во временном ряду. Ns – число серий.
При большом объеме временного ряда Т нормированная переменная z, определяемая как
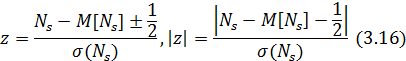
В этом случае для проверки гипотезы о стационарности используется двухсторонний критерий (3.6).
1. Кремер Н. Ш., Путко Б. А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2008
2. Практикум по эконометрике: Учебн. пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2009
3. Тихомиров Н.П., Дорохина Е.Ю. Эконометрика / Учебник. – М.: Изд-во Рос. экон. акад., 2008
4. Эконометрика. Учебник. Под ред. Елисеевой И.И. М., Финансы и статистика, 2010
 2015-04-23
2015-04-23 13133
13133