В транспортной задаче составить первоначальный план поставок и найти оптимальный план
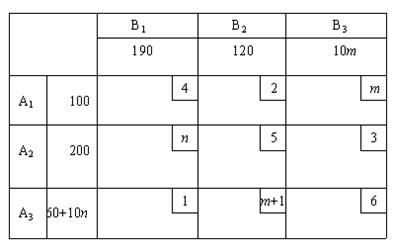
Решение
С учетом начального условия 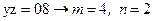 :
:
Таблица 3.1.
| Поставщики | Мощность поставщиков | Потребители и их спрос | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | ||||
| А3 |
Тогда задача водится к р ешению транспортной задачи вида
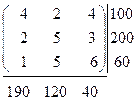 .
.
Для решения транспортной задачи необходимо
1) составить ее экономико-математическую модель и
2) найти оптимальное распределение поставок и минимальные затраты на перевозку.
Первоначальное распределение выполним методом наименьших затрат.
1. Экономико-математическая модель формулируется следующим образом: необходимо найти объемы перевозок для каждой пары «поставщик-потребитель» так, чтобы:
1) мощности всех поставщиков были реализованы;
2) спросы всех потребителей были удовлетворены;
3) суммарная стоимость затрат была минимальна.
1. Искомый объем перевозки от i-го поставщика к j-му потребителю обозначим 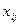 и назовем поставкой клетки (ij).
и назовем поставкой клетки (ij).
|
|
|
Заданные мощности поставщиков и спросы потребителей накладывают ограничения на значения 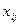 . Для реализации мощностей каждого поставщика и удовлетворения спроса потребителей составляем уравнения баланса для каждой строки и для каждого столбца таблицы поставок 3.2:
. Для реализации мощностей каждого поставщика и удовлетворения спроса потребителей составляем уравнения баланса для каждой строки и для каждого столбца таблицы поставок 3.2:
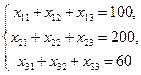 и
и 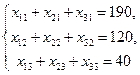
с ограничениями 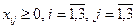 т.к. объем перевозок не может быть отрицательным.
т.к. объем перевозок не может быть отрицательным.
Таким образом, экономико-математическая модель задачи составлена.
2. Первоначальное распределение определяется методом потенциалов.
По условию задачи (см. таблицу 3.2) транспортная задача является открытой, т.к. суммарные мощности поставщиков 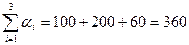 больше суммарного спроса потребителей
больше суммарного спроса потребителей 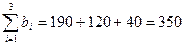 и часть поставщиков останется незагруженными.
и часть поставщиков останется незагруженными.
Для баланса спроса и предложения и для приведения системы к закрытому типу вводим фиктивного потребителя 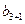 с нулевыми условными затратами на перевозку и объемом спроса, равным разности объемов поставок и потребления
с нулевыми условными затратами на перевозку и объемом спроса, равным разности объемов поставок и потребления
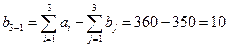 .
.
Таблица 3.2 – таблица поставок.
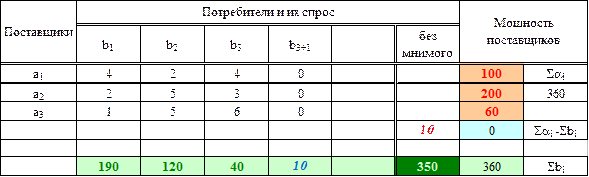
Находим в таблице поставок клетки с наименьшей ненулевой стоимостью затрат: (3.1)) и анализируем возможности поставок для этой клетки:
для клетки (3.1): 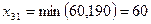 ;
;
для клетки (1.4): 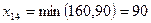 ;
;
для клетки (1.1): 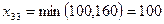 ;
;
Минимальную из максимально возможных поставок 60 для потребителя 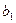 даем в клетку (3.1), поставку 190-60=130 даем в клетку (2.1) и исключаем из рассмотрения третью строку и первый столбец.
даем в клетку (3.1), поставку 190-60=130 даем в клетку (2.1) и исключаем из рассмотрения третью строку и первый столбец.
В оставшейся части таблицы поставок наименьшими затратами, равными 2, обладает клетка (1.2) с максимальной возможностью поставок 100. Отдаем поставку 100 для потребителя 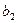 в клетку (1.2), оставшуюся часть поставки 120-100=20 даем в клетку (2.2) и исключаем из рассмотрения второй столбец
в клетку (1.2), оставшуюся часть поставки 120-100=20 даем в клетку (2.2) и исключаем из рассмотрения второй столбец
В оставшейся части таблицы наименьшие затраты 3 с максимальной (остаточной) возможностью поставок 200-130-20=50 имеет клетка (3.2). Для удовлетворения потребителя 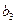 отдаем поставку 40 в клетку (3.2) и исключаем из рассмотрения 3 столбец.
отдаем поставку 40 в клетку (3.2) и исключаем из рассмотрения 3 столбец.
|
|
|
При этом поставщик 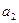 останется недогруженным в объеме 50-40=10 единиц.
останется недогруженным в объеме 50-40=10 единиц.
Таблица поставок
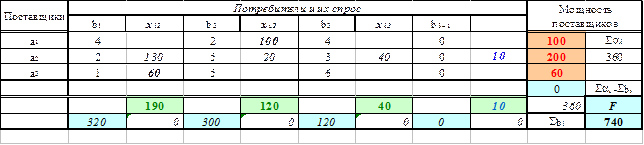
Минимальные затраты на перевозку согласно таблицы поставок составят
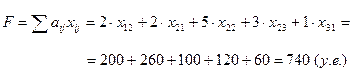
Ответ: Минимальные затраты на перевозку согласно таблицы поставок составят 740 у.е.
4. A={aij}‑ матрица прямых материальных затрат, y – вектор конечного выпуска. Требуется:
1) Построить таблицу межотраслевого баланса в стоимостном выражении.
2) Найти изменение валовых выпусков при увеличении конечного выпуска первой отрасли на 20%, третьей – на 25% и неизменном выпуске второй отрасли.
| № | а11 | а12 | а13 | а21 | а22 | а23 | а31 | а32 | а33 | y1 | y2 | y3 |
| 22 | 0,1 | 0,2 | 0,1 | 0,2 | 0,1 | 0,0 | 0,0 | 0,2 | 0,1 | 100 | 200 | 300 |
Задача об инвестировании предприятий. Капитал в 5 условных д.е. требуется распределить между четырьмя предприятиями. Номер варианта совпадает с номером студента в списке группы. каждый вариант представляет собой таблицу размера 5´4. Строки таблицы соответствуют размеру инвестиций х, которые может получить предприятие, х =1, 2, 3, 4 или 5 условных д.е. соответственно. Столбцы таблицы соответствуют прибыли, котрую принесут
1-е, 2-е, 3-е и 4-е предприятие соответственно, при таком объеме инвестиций. (строку с нулевой прибылью, соответствующей х =0, добавить самостоятельно).
Найти распределение инвестиций, обеспечивающее максимальную суммарную прибыль от четырех предприятий вместе
Систему уравнений, представляющих собой соотношения баланса, можно записать в матричном виде:
X = AX + Y,
где A – матрицей прямых затрат, X – вектор валового выпуска, Y – вектор конечного продукта.
Основная цель межотраслевого баланса состоит в том, чтобы отыскать такой вектор X, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта Y.
Система уравнений межотраслевого баланса легко решается методом обратной матрицы. Действительно,
X = AX + Y Þ EX = AX + Y Þ EX - AX = Y Þ (E – A)X = Y Þ
|
Þ (E-A)-1 (E – A)X = (E – A)-1 Y Þ EX = (E – A)-1 Y Þ.
где матрица S = (E – A)-1 называется матрицей полных затрат.
В соответствии с введенными обозначениями имеем:
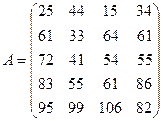 ,
, 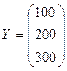
В задаче требуется найти такой вектор X, который при матрице А дал бы вектор конечного продукта.
Найдем матрицу E – A:
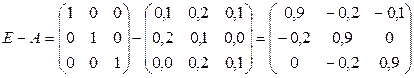
Определитель этой матрицы:
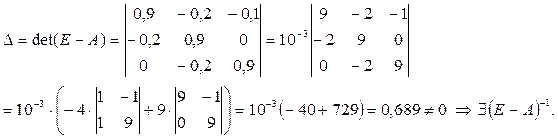 .
.
Найдем алгебраические дополнения Aij к элементам матрицы E – A:
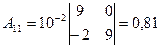 ,
, 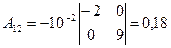 ,
, 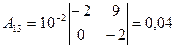 ,
,
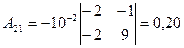 ,
, 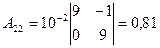 ,
, 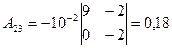 ,
,
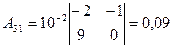 ,
, 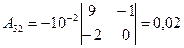 ,
, 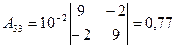
Присоединенная матрица, т.е. транспонированная матрица алгебраических дополнений:
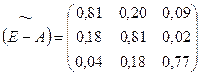
Тогда обратная матрица (E – A) -1 имеет вид:

Находим искомый вектор X:
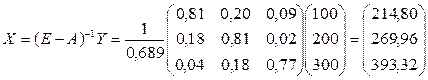 .
.
Проверим правильность нахождения обратной матрицы и вектора Х, применяя функции Microsoft Office System Professional 2003 «МОПРЕД», «МОБР», «МУМНОЖ»:

Таким образом, объем валового продукта для 1 отрасли составит 214,8 условных денежных единиц, 2 отрасли – 269,96 условных денежных единиц, а 3 отрасли – 393,32 условных денежных единиц.
Для построения таблицы межотраслевого баланса в стоимостном выражении необходимо определить величины xij – часть объема продукции i-той отрасли, потребляемая j-той отраслью
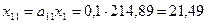 ,
, 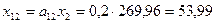 ,
, 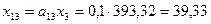 ,
,
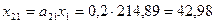 ,
, 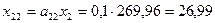 ,
, 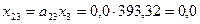 ,
,
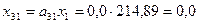 ,
, 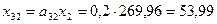 ,
, 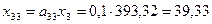 .
.
Таблица межотраслевого баланса в стоимостном выражении
| Отрасль | Потребление | Конечный продукт | Валовой продукт | |||
| 1 | 2 | 3 | ||||
| Производство | 1 | 21,49 | 53,99 | 39,33 | 100 | 214,80 |
| 2 | 42,98 | 26,99 | 0,0 | 200 | 269,96 | |
| 3 | 0,0 | 53,99 | 39,33 | 300 | 393,32 |
Данная таблица означает, что 1 отрасль производит 214,8 условных денежных единиц продукции, из них тратятся на нужды 1 отрасли 21,49 у.е., на нужды 2 отрасли 53,99 у.е., на нужды 3 отрасли 39,33 у.е. и 100 у.е. идут на потреблении; 2 отрасль производит 269,96 у.е. продукции, из них тратится на нужды 1 отрасли 42,98 у.е., на нужды 2 отрасли 26,99 у.е. и 200 у.е. идут на потребление; 32 отрасль производит 393,32 у.е. продукции, из них тратится на нужды 2 отрасли 53,99 у.е., на нужды 3 отрасли 39,33 у.е. и 300 у.е. идут на потребление.
|
|
|
2) Для того, чтобы вычислить изменение валовых выпусков при увеличении конечного выпуска первой отрасли на 20%, третьей – на 25% и неизменном выпуске второй отрасли, необходимо найти такой вектор 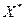 , который при матрице А дал бы вектор конечного продукта
, который при матрице А дал бы вектор конечного продукта 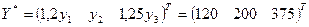 .
.
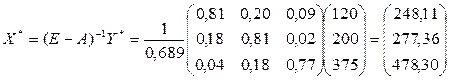 .
.
| Отрасль | Потребление | Конечный продукт | Валовой продукт | Абсолютное изменение ВП | Относительное изменение ВП | |||
| 1 | 2 | 3 | ||||||
| Производство | 1 | 21,49 | 53,99 | 39,33 | 120 | 248,11 | 33,31 | 15,51% |
| 2 | 42,98 | 26,99 | 0,0 | 200 | 277,36 | 7,40 | 2,74% | |
| 3 | 0,0 | 53,99 | 39,33 | 375 | 478,30 | 84,98 | 21,61% |
Таблица изменений межотраслевого баланса в стоимостном выражении
Ответ: валовой выпуск увеличится в 1 отрасли на 15,51%, во 2 отрасли – на 2,74%, а в 3 отрасли – на 21,61% и составит 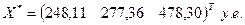
Задача №2. Решить задачу симплекс-методом.
Для производства двух видов изделий - изделий А и изделий В - предприятие использует три вида сырья.
Нормы расхода сырья каждого вида на изготовление единицы продукции приведены в таблице. В ней же указана прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.
Учитывая, что изделия А и В могут производиться в любых соотношениях (спрос обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий максимальна.
Таблица 2.1.
| Вид сырья | Нормы расхода сырья (кг) на одно изделие | Общее количество сырья (кг) | |
| А | В | ||
| Прибыль от реализации одного изделия (руб.) |
Решение.
Данные, представленные в таблице 1 удобно представить в виде
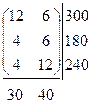
Задачу можно решить симплекс-методом ЗЛП. Для этого сформулируем задачу и запишем условие в каноническом виде.
1. Из анализа условия задачи следует, что целевая функция ЗЛП имеет вид
Q = 30x 1 + 40x 2 ® max (1)
при ограничениях:
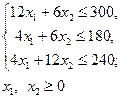 (2)
(2)
2. Приводим ЗЛП к каноническому виду, вводя по числу неравенств неотрицательные переменные x 5, x 6 и x 7 со знаком «+», так как все неравенства системы (1) 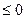 :
:
Q = 30x 1 + 40x 2 + 0×x 3 + 0×x 4 + 0×x 5 ® max (3)
|
|
|
при ограничениях:
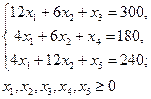 (4)
(4)
Для нахождения начального опорного плана нужно найти общее решение системы ограничений, но такое, чтобы все свободные члены (4) bi были неотрицательными.
Второе уравнение имеет предпочтительный вид, в то время как остальные уравнения его не имеют. Для нахождения допустимого общего решения системы ограничений применим метод Жордана. Удобно это делать, записав систему ограничений в виде симплекс-таблицы.
Для нахождения общего решения методом Жордана необходимо на каждом шаге выбирать разрешающий элемент. Чтобы соблюсти при этом условие неотрицательности свободных членов, для каждого положительного коэффициента aij рассчитываем 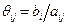 .
.
При этом, если коэффициент aij £ 0, то qij не вычисляем, а в соответствующей клетке таблицы ставим прочерк. Затем произвольно выбираем разрешающую строку (кроме строки, соответствующей уравнению в предпочтительном виде), а разрешающим столбцом выбираем тот, в котором в разрешающей строке находится наименьшее в этом столбце значение qij.
3. За базисные (основные) переменные принимаем x 5; x 6; x 7, исходные переменные – за свободные переменные, причем x 1 = 0; x 2 = 0; x 3 = 0; x 4 = 0. Выражая 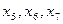 через свободные переменные
через свободные переменные
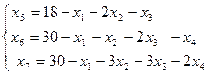
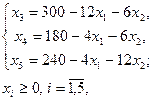 (5)
(5)
и подставляя значения x 1 = 0; x 2 = 0; x 3 = 0 в систему (5) получим x 3 =300; x 4 =180; x 5 =240. Таким образом, первый опорный план имеет вид:
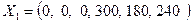 ,
,
а функция 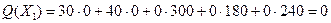 .
.
4. Для проверки оптимальности начального опорного плана составляем симплекс-таблицу 2.2.
Симплекс-таблица 2.2
| Базис | cj | 30 | 40 | 0 | 0 | 0 |  | 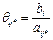 j*=2 j*=2 | ||
| xi | i | ci | bi | ai1 | ai2 | ai3 | ai4 | ai5 | ||
| x3 | 3 | |||||||||
| x4 | 4 | |||||||||
 x5 x5 | 5 | |||||||||
| Dj | D0=0 | – 30 | – 40  | 0 | 0 | 0 | 779 | 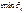 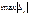 |
Для базисных неизвестных величины D j = 0. Поэтому подсчитываем
D 0 = Q и D 1,2,3,4,5 .: 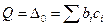 ,
, 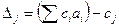
Q (Х1)= D 0 = 300× 0 + 180× 0 + 240 × 0 = 0;
D 1 = 0×12 + 0 × 4 + 0 × 4 – 30 = – 30;
D 2 = 0×6 + 0 × 6 + 0 × 12 – 40 = – 40;
D 3 = 0×1 + 0 × 0 + 0 × 0 – 0 = 0;
D 4 = 0×0 + 0 × 1 + 0 × 0 – 0 = 0.
D 5 = 0×0 + 0 × 0 + 0 × 1 – 0 = 0.
Поскольку в индексной строке Dj имеются отрицательные числа
D 1 =–30, D 2 = – 40, то начальный опорный план не является оптимальным.
5. Находим направляющий столбец и направляющую строку.
Направляющему столбцу соответствует максимальный по модулю отрицательный элемент индексной строки 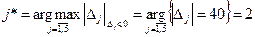 . Следовательно, переменную
. Следовательно, переменную 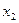 следует перевести из свободных в базисные.
следует перевести из свободных в базисные.
Направляющей строке соответствует минимальное значение 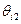 :
: 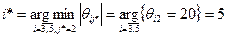 . Следовательно, переменную
. Следовательно, переменную 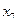 следует перевести из базисных в свободные.
следует перевести из базисных в свободные.
Разрешающим является элемент 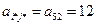 . Направляющие строка и столбец обозначены в симплекс-таблице 2.1 стрелками.
. Направляющие строка и столбец обозначены в симплекс-таблице 2.1 стрелками.
6. Для определения нового опорного плана формируем симплекс-таблицу 2.3.
На место переменной 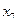 в столбце «Базис,
в столбце «Базис, 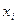 » ставим переменную
» ставим переменную 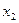 , в разрешающую строку в столбце «Базис,
, в разрешающую строку в столбце «Базис, 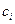 » записываем значение
» записываем значение 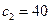 коэффициента целевой функции при переменной
коэффициента целевой функции при переменной 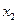 , остальные элементы строки
, остальные элементы строки 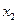 получаются делением элементов строки
получаются делением элементов строки 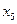 на разрешающий элемент
на разрешающий элемент 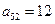 .
.
В симплекс-таблице 2.3 элемент 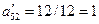 , а остальные элементы разрешающего столбца полагаем равными 0. Оставшиеся элементы строк
, а остальные элементы разрешающего столбца полагаем равными 0. Оставшиеся элементы строк 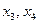 вычисляем по правилу прямоугольника
вычисляем по правилу прямоугольника 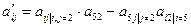 .
.
Симплекс-таблица 2.3
| Базис | cj | 30 | 40 | 0 | 0 | 0 | 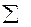 | 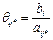 j*=1 j*=1 | ||
| xi | i | ci | bi | ai1 | ai2 | ai3 | ai4 | ai5 | ||
 x3 x3 | 3 | 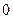 | 0 | -0,5 | 190,5 | |||||
| x4 | 4 | 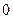 | 1 | -0,5 | 62,5 | |||||
| x2 | 2 | 0,3 | 0,08 | 63,38 | ||||||
| Dj | D0=800 | – 26,(7)  | 0 | 0 | 0 | 3,(3) | 316,38 | 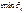 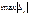 |
Новый опорный план имеет вид: 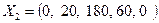 .
.
Для новых базисных неизвестных 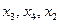 величины D 3,4,2 = 0. Подсчитываем D 0 = Q; D j, где
величины D 3,4,2 = 0. Подсчитываем D 0 = Q; D j, где 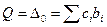 ,
, 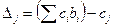 :
:
Q (Х2)= D 0 =0 ×180 + 0×60+ 40×20= 800;
D 1 = 0×10 + 0 × 2 + 40×1/3 – 30 = – 16,(7);
D 2 = 0×0 + 0 × 0 + 40 × 1 – 40 = 0;
D 3 = 0×1 + 0 × 0 +4 0 × 0 – 0 = 0;
D 4 = 0×0 + 0 × 1 + 40 × 0 – 0 = 0.
D 5 = 0×(-1/12) + 0 × (-1/12) + 40 × 1/12 – 0 = 3,(3).
В индексной строке имеется отрицательное число D 1 = – 16,(7), поэтому полученный опорный план не является оптимальным.
7. Для определения нового (третьего) опорного плана формируем симплекс-таблицу 2.4.
Направляющий столбец и направляющую строку ищем аналогично п.5.
Направляющему столбцу соответствует максимальный по модулю отрицательный элемент индексной строки 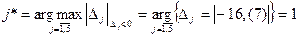 . Следовательно, переменную
. Следовательно, переменную 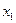 следует перевести из свободных в базисные.
следует перевести из свободных в базисные.
Направляющей строке соответствует минимальное значение 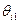 :
: 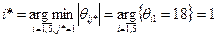 . Следовательно, переменную
. Следовательно, переменную 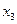 следует перевести из базисных в свободные.
следует перевести из базисных в свободные.
Разрешающим является элемент 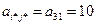 . Направляющие строка и столбец обозначены в симплекс-таблице 2.2 стрелками.
. Направляющие строка и столбец обозначены в симплекс-таблице 2.2 стрелками.
На место переменной 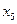 в столбце «Базис,
в столбце «Базис, 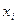 » ставим переменную
» ставим переменную 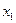 , в разрешающую строку в столбце «Базис,
, в разрешающую строку в столбце «Базис, 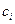 » записываем значение
» записываем значение 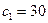 коэффициента целевой функции при переменной
коэффициента целевой функции при переменной 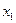 , остальные элементы строки
, остальные элементы строки 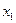 получаются делением элементов строки
получаются делением элементов строки 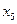 на разрешающий элемент
на разрешающий элемент 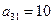 .
.
В симплекс-таблице 2.3 элемент 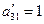 , а остальные элементы разрешающего столбца полагаем равными 0. Оставшиеся элементы строк
, а остальные элементы разрешающего столбца полагаем равными 0. Оставшиеся элементы строк 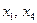 вычисляем по правилу прямоугольника
вычисляем по правилу прямоугольника 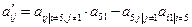 .
.
Симплекс-таблица 2.4.
| Базис | cj | 30 | 40 | 0 | 0 | 0 | 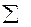 | 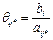 j*=4 j*=4 | ||
| xi | i | ci | bi | ai1 | ai2 | ai3 | ai4 | ai5 | ||
| x1 | 1 | 0,1 | 0 | –0,05 | 50,15 | – | ||||
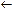 x4 x4 | 4 | 0 | –0,4 | 62,5 | – | |||||
| x2 | 3 | –0,03 | 0,18 | 63,38 | – | |||||
| Dj | D0=1100 | 0 | 0 | 1,8 | 0 | 5,7 | 176,03 | 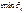 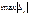 |
Новый опорный план имеет вид: 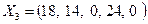 .
.
Для новых базисных неизвестных 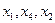 величины D 1,4,2 = 0. Подсчитываем D 0 = Q; D j, где
величины D 1,4,2 = 0. Подсчитываем D 0 = Q; D j, где 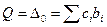 ,
, 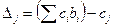 :
:
Q (Х3)= D 0 =30 ×18 + 0×24+ 40×14= 1100;
D 1 =30×18 + 0 × 0 + 40×0 – 30 =0;
D 2 = 30×0 + 0 × 0 + 40 × 1 – 40 = 0;
D 3 = 30×1 + 0 × 0 +40 × (-0,03) – 0 = 1,8;
D 4 = 30×0 + 0 × 1 + 40 × 0 – 0 = 0.
D 5 = 30×(-0,05) + 0 × (-0,4) + 40 × 0,18 – 0 = 5,7.
В индексной строке нет отрицательных чисел, поэтому полученный опорный план Х3 является оптимальным. При этом Q max = 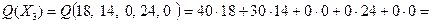 1100 (руб.).
1100 (руб.).
Ответ: x* = (18; 14). Q max = 1100 руб.
Задача №4. Для платёжной матрицы
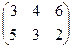
определить нижнюю и верхнюю цены игры, проверить, существует ли седловая точка. А также:
а) графически определить чистую цену игры и оптимальную стратегию
стороны А;
б) графически определить чистую цену игры и оптимальную стратегию
стороны В.
№3. Найти оптимальные стратегии и цену игры, заданной матрицей
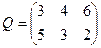 .
.
Решение.
В задаче рассматривается антагонистическая игра партнеров-соперников А и В, имеющих в своем распоряжении, соответственно, n=2 и m=3 стратегии. При этом заданная платежная матрица игры имеет вид:
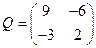 .
.
Основное допущение теории игр состоит в том, что каждый игрок стремиться обеспечить себе максимально возможный выигрыш при любых действиях других игроков. Если матрица выигрышей игрока А – это Q, тогда для игрока В – это –Q. Игрок А полагает, что В выберет стратегию, обеспечивающую его выигрыш (минимизирующий выигрыш игрока А)., т.е. стратегия игрока А состоит в выборе строки и в ней элемента матрицы Q, которая согласно максминной стратегии обеспечивает выигрыш не меньший нижней цены игры
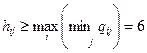 .
.
Для игрока В стратегия минимаксная, его проигрыш не будет превосходить величины верхней цены игры 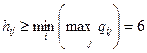
.
Если верхняя цена игры равна нижней, то значение 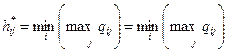 представляет собой цену игры, а элемент
представляет собой цену игры, а элемент 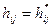 – это седловая точка матрицы Q/
– это седловая точка матрицы Q/
Решение игры определяется следующими вероятностями:
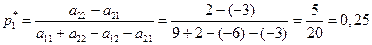 ;
;
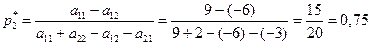 ;
;
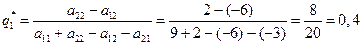 ;
;
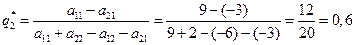 .
.
Таким образом, 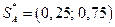 ;
; 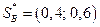 .
.
Полученный результат означает, что оптимальная смешанная стратегия игрока А состоит в том, чтобы применять чистые стратегии A1 и A2 случайным образом с вероятностями соответственно 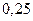 и
и 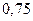 , а игрока В – чистые стратегии В1 и В2 – с вероятностями
, а игрока В – чистые стратегии В1 и В2 – с вероятностями 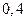 и
и 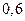 . Найдем цену игры с, т.е. средний выигрыш игрока А при оптимальных смешанных стратегиях:
. Найдем цену игры с, т.е. средний выигрыш игрока А при оптимальных смешанных стратегиях:
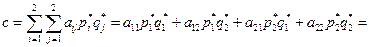
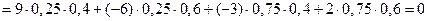 .
.
Цена игры, т.е. средний выигрыш игрока А, равен нулю. Следовательно, эта игра невыгодна ни для игрока А, ни для игрока В.
Ответ: 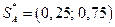 ;
; 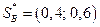 ; с=0.
; с=0.
 2015-05-18
2015-05-18 2701
2701