Дифференциальное исчисление функций одной переменной
План:
1. Производная функции
3. Приложение дифференциального исчисления к исследованию функции
Производная функции одной переменной
Пусть функция 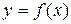 определена на некотором интервале
определена на некотором интервале 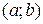 . Аргументу
. Аргументу 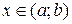 дадим приращение
дадим приращение 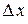 :
: 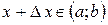 , тогда функция получит приращение
, тогда функция получит приращение 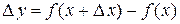 . Найдем предел этого отношения при
. Найдем предел этого отношения при 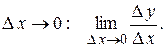 Если этот предел существует, то его называют производной функции
Если этот предел существует, то его называют производной функции 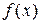 . Производная функции имеет несколько обозначений:
. Производная функции имеет несколько обозначений: 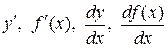 . Иногда в обозначении производной используется индекс
. Иногда в обозначении производной используется индекс 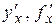 , указывающий, по какой переменной взята производная.
, указывающий, по какой переменной взята производная.
Определение. Производной функции 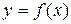 в точке
в точке 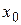 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (если этот предел существует):
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (если этот предел существует):
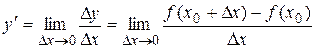 .
.
Определение. Функция 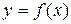 , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала 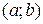 , называется дифференцируемой в этом интервале.
, называется дифференцируемой в этом интервале.
Определение. Операция нахождения производной функции называется дифференцированием.
Значение производной функции 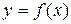 в точке
в точке 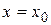 обозначается одним из символов:
обозначается одним из символов: 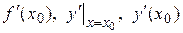 .
.
Пример. Найти производную функции 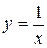 в произвольной точке
в произвольной точке 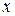 .
.
Решение. Значению 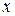 даем приращение
даем приращение 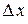 . Найдем приращение функции в точке
. Найдем приращение функции в точке 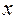 :
: 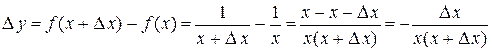 . Составим отношение
. Составим отношение 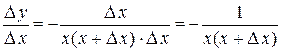 . Перейдем к пределу:
. Перейдем к пределу: 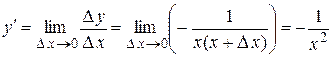 . Таким образом,
. Таким образом, 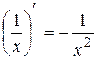 .
.
Механический смысл производной. Так как 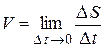 или
или 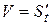 , т.е. скорость прямолинейного движения материальной точки в момент времени
, т.е. скорость прямолинейного движения материальной точки в момент времени  есть производная от пути
есть производная от пути 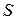 по времени
по времени  . В этом заключается механический смысл производной.
. В этом заключается механический смысл производной.
Если функция 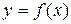 описывает какой-либо физический процесс, то производная
описывает какой-либо физический процесс, то производная 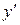 есть скорость протекания этого процесса. В этом состоит физический смысл производной.
есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Геометрический смысл производной. Рассмотрим график непрерывной кривой 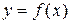 , имеющий в точке
, имеющий в точке 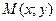 невертикальную касательную. Найдем ее угловой коэффициент
невертикальную касательную. Найдем ее угловой коэффициент 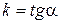 , где
, где 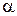 - угол касательной с осью
- угол касательной с осью 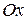 . Для этого проведем через точку
. Для этого проведем через точку 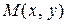 и
и 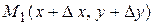 графика секущую (рисунок 1).
графика секущую (рисунок 1).
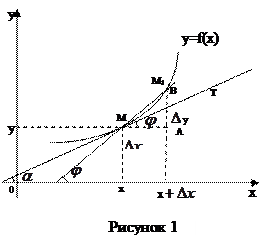
Обозначим через 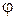 - угол между секущей
- угол между секущей 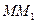 и осью
и осью 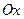 . На рисунке видно, что угловой коэффициент секущей равен
. На рисунке видно, что угловой коэффициент секущей равен
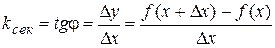 .
.
При 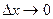 в силу непрерывности функции приращение
в силу непрерывности функции приращение 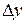 тоже стремится к нулю; поэтому точка
тоже стремится к нулю; поэтому точка 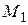 неограниченно приближается по кривой к точке
неограниченно приближается по кривой к точке 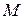 , а секущая
, а секущая 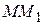 , поворачиваясь около точки
, поворачиваясь около точки 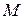 , переходит в касательную. Угол
, переходит в касательную. Угол 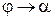 , т.е.
, т.е. 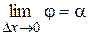 . Следовательно,
. Следовательно, 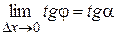 , поэтому угловой коэффициент касательной равен
, поэтому угловой коэффициент касательной равен 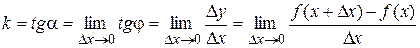 .
.
Угловой коэффициент касательной к кривой
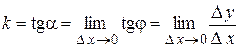 . Это равенство перепишем в виде:
. Это равенство перепишем в виде: 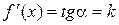 , т.е. производная
, т.е. производная 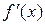 в точке
в точке 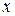 равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции 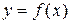 в точке, абсцисса которой равна
в точке, абсцисса которой равна 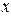 . В этом заключается геометрический смысл производной.
. В этом заключается геометрический смысл производной.
Если точка касания 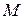 имеет координаты
имеет координаты 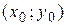 (рисунок 2), угловой коэффициент касательной равен:
(рисунок 2), угловой коэффициент касательной равен: 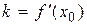 .
.

Уравнение прямой проходящей через заданную точку в заданном направлении имеет вид: 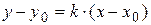 .
.
Тогда уравнение касательной записывается в виде: 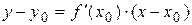 .
.
Определение. Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Угловой коэффициент нормали равен: 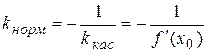 (так как нормаль перпендикулярна касательной).
(так как нормаль перпендикулярна касательной).
Уравнение нормали имеет вид: 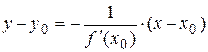 , если
, если 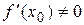 .
.
Подставляя найденные значения 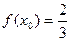 и
и 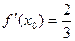 получаем уравнения касательной
получаем уравнения касательной 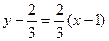 , т.е.
, т.е. 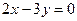 .
.
Уравнение нормали: 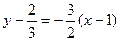 или
или 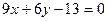 .
.
Если функция имеет конечную производную в точке, то она дифференцируема в этой точке. Если функция дифференцируема в каждой точке интервала, то она дифференцируема в этом интервале.
Теорема 6.1 Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Обратная теорема неверна. Непрерывная функция может не иметь производной.
Пример. Функция 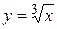 непрерывна на интервале
непрерывна на интервале 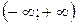 (рисунок 3).
(рисунок 3).
Решение.
Производная этой функции равна:

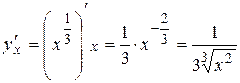 .
.
В точке 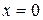
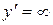 - функция не дифференцируема.
- функция не дифференцируема.
Замечание. На практике чаще всего приходится находить производные от сложных функций. Поэтому в таблице формул дифференцирования аргумент 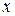 заменен на промежуточный аргумент
заменен на промежуточный аргумент 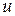
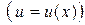 .
.
Таблица производных
Постоянная величина
1) 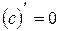 ;
;
Степенная функция 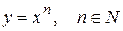 :
:
2) 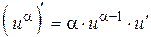 , в частности
, в частности 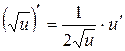 ;
;
Показательная функция 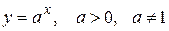 :
:
3) 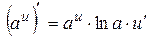 , в частности
, в частности 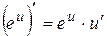 ;
;
4) 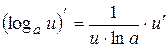 , в частности,
, в частности, 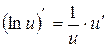 ;
;
5) 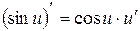 ;
;
6) 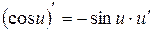 ;
;
7) 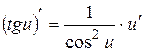 ;
;
8) 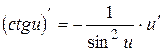 ;
;
Обратные тригонометрические функции 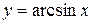 ,
, 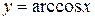 ,
, 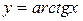 ,
, 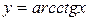 :
:
9) 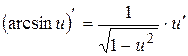 ;
;
10) 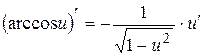 ;
;
11) 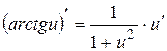 ;
;
12) 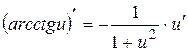 ;
;
Продифференцировать функцию это значит найти ее производную, то есть вычислить предел: 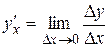 . Однако определение предела в большинстве случаев представляет громоздкую задачу.
. Однако определение предела в большинстве случаев представляет громоздкую задачу.
Если знать производные основных элементарных функций и знать правила дифференцирования результатов арифметических действий над этими функциями, то можно легко найти производные любых элементарных функций, согласно правил определения производных, хорошо известных из школьного курса.
Пусть функции 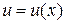 и
и 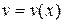 - две дифференцируемые в некотором интервале
- две дифференцируемые в некотором интервале 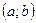 функции.
функции.
Теорема 6.2 Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: 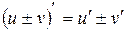 .
.
Теорема справедлива для любого конечного числа слагаемых.
Пример. Найти производную функции 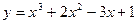 .
.
Решение. 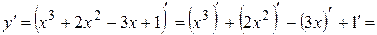
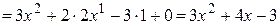 .
.
Теорема 6.3 Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: 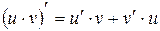 .
.
Пример. Найти производную функции 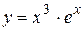 .
.
Решение. 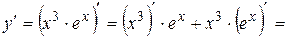
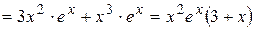 .
.
Теорема 6.4 Производная частного двух функций 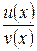 , если
, если 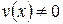 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя:
равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: 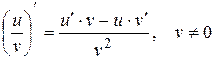 .
.
Пример. Найти производную функции 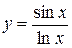 .
.
Решение. 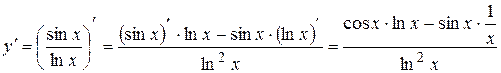 .
.
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу
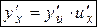 . (1)
. (1)
Это правило остается в силе, если промежуточных аргументов несколько. Так, если 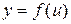 ,
, 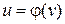 ,
, 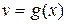 , то
, то
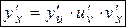 . (2)
. (2)
Пусть 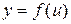 и, тогда
и, тогда 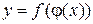 - сложная функция с промежуточным аргументом
- сложная функция с промежуточным аргументом 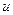 и независимым аргументом
и независимым аргументом 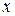 .
.
Теорема 6.5 Если функция 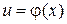 имеет производную
имеет производную 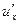 в точке
в точке 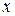 , а функция
, а функция 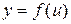 имеет производную
имеет производную 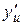 в соответствующей точке
в соответствующей точке 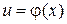 , то сложная функция
, то сложная функция 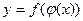 имеет производную
имеет производную 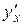 в точке
в точке 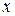 , которая находится по формуле
, которая находится по формуле 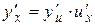 .
.
Теорема 6.6 Если функция 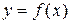 строго монотонна на интервале
строго монотонна на интервале 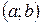 и имеет неравную нулю производную
и имеет неравную нулю производную 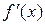 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 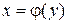 также имеет производную
также имеет производную 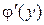 в соответствующей точке, определяемую равенством
в соответствующей точке, определяемую равенством 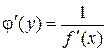 или
или 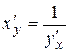 .
.
1) 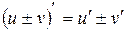 ;
;
2) 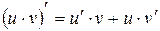 ,
, 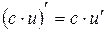 ;
;
3) 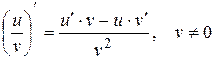 ,
, 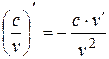 ;
;
4) 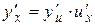 , если
, если 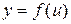 ,
, 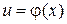 ;
;
5) 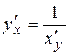 , если
, если 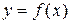 ,
, 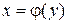 .
.
Определение. Если функция задана уравнением 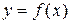 , разрешенным относительно
, разрешенным относительно 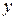 , то функция задана в явном виде (явная функция).
, то функция задана в явном виде (явная функция).
Определение. Неявная функция одного аргумента задается уравнением, связывающим две переменные, причем уравнение не разрешено относительно какой-либо из них: 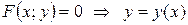 или
или 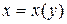 .
.
Определение. Уравнение, связывающее три переменные, задает неявную функцию 2 аргументов: 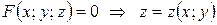 , или
, или 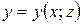 , или
, или 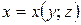 .
.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно 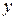 (например,
(например, 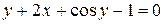 или
или 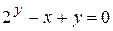 ).
).
Если неявная функция задана уравнением 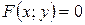 , то для нахождения производной от
, то для нахождения производной от 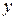 по
по 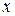 нет необходимости разрешать уравнение относительно
нет необходимости разрешать уравнение относительно 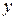 . Нужно продифференцировать это уравнение по
. Нужно продифференцировать это уравнение по 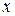 , рассматривая при этом
, рассматривая при этом 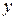 как функцию
как функцию 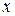 , и полученное затем уравнение разрешить относительно
, и полученное затем уравнение разрешить относительно 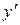 .
.
Пример. Найти производную функции 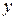 , заданную уравнением:
, заданную уравнением: 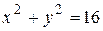 .
.
Решение. Функция 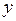 задана неявно. Продифференцируем уравнение по
задана неявно. Продифференцируем уравнение по 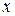 , помня, что
, помня, что 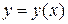 :
: 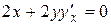 . Затем находим:
. Затем находим: 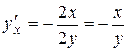 .
.
 2015-05-13
2015-05-13 16183
16183
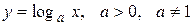 :
: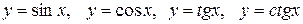 :
: