Функциональный ряд
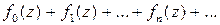 (1)
(1)
сходится в области 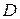 , если при любом
, если при любом 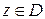 соответствующий этому значению
соответствующий этому значению 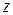 числовой ряд является сходящимся.
числовой ряд является сходящимся.
Пусть ряд (1) сходится в области 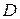 , тогда функция
, тогда функция 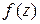 , значение которой в каждой точке
, значение которой в каждой точке 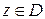 равно сумме соответствующего числового ряда, называется суммой ряда (1) в области
равно сумме соответствующего числового ряда, называется суммой ряда (1) в области 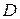 .
.
Если ряд (1) сходится в 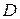 , то для любой фиксированной точки
, то для любой фиксированной точки 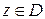 и для любого
и для любого 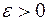 можно указать такой номер
можно указать такой номер 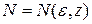 , начиная с которого для всех
, начиная с которого для всех 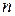 выполняется неравенство
выполняется неравенство
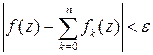 .
.
Если обозначить 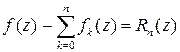 – остаток ряда, то неравенство принимает вид
– остаток ряда, то неравенство принимает вид 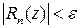 при
при 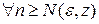 . Запись
. Запись 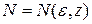 подчеркивает, что номер
подчеркивает, что номер 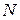 , вообще говоря, не является одинаковым для всех точек
, вообще говоря, не является одинаковым для всех точек 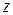 области сходимости ряда.
области сходимости ряда.
Определение. Если для любого 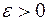 можно указать такой номер
можно указать такой номер 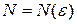 , что при
, что при 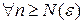 неравенство
неравенство 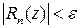 выполняется сразу для всех точек
выполняется сразу для всех точек 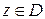 , то ряд (1) называется равномерно сходящимся в области
, то ряд (1) называется равномерно сходящимся в области 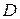 .
.
Если члены ряда (1) являются аналитическими функциями в односвязной области 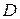 и ряд сходится в этой области равномерно, то сумма ряда
и ряд сходится в этой области равномерно, то сумма ряда 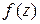 также является функцией, аналитической в области
также является функцией, аналитической в области 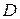 (теорема Вейерштрасса). В этом случае ряд можно дифференцировать почленно сколько угодно раз.
(теорема Вейерштрасса). В этом случае ряд можно дифференцировать почленно сколько угодно раз.
|
|
|
Пример 1. Исследовать сходимость ряда 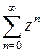 . Найти сумму этого ряда.
. Найти сумму этого ряда.
Решение. Формула для суммы 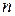 членов геометрической прогрессии
членов геометрической прогрессии

 (2)
(2)
справедлива при любом комплексном 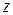 . Так как
. Так как 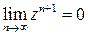 , если
, если 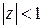 и
и 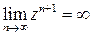 , если
, если 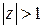 , то получаем
, то получаем 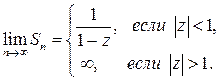
Но сумма (2) является частичной суммой заданного ряда. Значит, заданный ряд
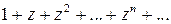 (3)
(3)
сходится внутри круга 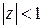 и сумма этого ряда равна
и сумма этого ряда равна
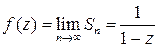 .
.
Вне единичного круга (при 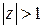 ) этот ряд расходится. На окружности
) этот ряд расходится. На окружности 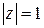 ряд (3) также расходится, так как
ряд (3) также расходится, так как 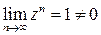 – не выполнено необходимое условие сходимости.
– не выполнено необходимое условие сходимости.
Заметим, что в круге 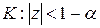 ,
, 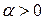 ряд (3) сходится равномерно. ☻
ряд (3) сходится равномерно. ☻
Ряд вида
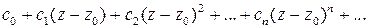 , (4)
, (4)
где 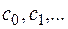 – комплексные постоянные, называется степенным рядом (с центром в точке
– комплексные постоянные, называется степенным рядом (с центром в точке 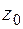 ).
).
Основной теоремой теории степенных рядов является
Теорема Абеля. Если степенной ряд (4) сходится в точке 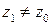 , то он сходится и притом абсолютно во всех точках
, то он сходится и притом абсолютно во всех точках 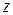 , для которых
, для которых 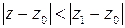 . В замкнутой области
. В замкнутой области 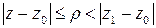 ряд сходится равномерно.
ряд сходится равномерно.
Геометрически: если ряд (4) сходится в точке 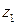 , то он сходится абсолютно в круге с центром в точке
, то он сходится абсолютно в круге с центром в точке  радиуса
радиуса 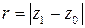 , причем в круге
, причем в круге 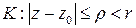 этот ряд сходится равномерно. Если же ряд расходится в некоторой точке
этот ряд сходится равномерно. Если же ряд расходится в некоторой точке 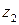 , то он расходится и при любых
, то он расходится и при любых 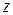 , для которых
, для которых 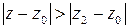 .
.
Область сходимости степенного ряда (4) есть круг с центром в точке  , радиус которого определяется по формуле Коши-Адамара
, радиус которого определяется по формуле Коши-Адамара
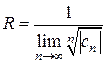 (5)
(5)
или по формуле
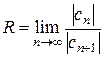 (6)
(6)
Пример 2. Найти область сходимости степенного ряда 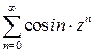 .
.
Решение. Здесь 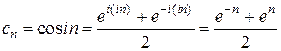 . По формуле (5) находим радиус сходимости данного ряда:
. По формуле (5) находим радиус сходимости данного ряда:

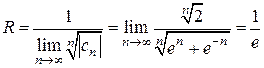 .
.
Здесь учтено, что 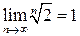 .
.
Можно получить тот же результат с помощью формулы (6):
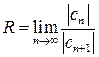
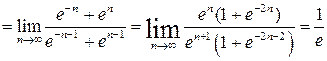 .
.
Значит, область сходимости данного ряда – круг 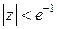 . ☻
. ☻
Задача 1. Показать, что областью сходимости ряда 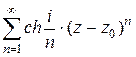 является круг
является круг 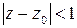 .
.
|
|
|
Пример 3. Найти область сходимости степенного ряда 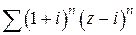 .
.
Сходится ли этот ряд в точке 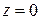 ?
?
Решение. Здесь 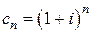 , значит,
, значит, 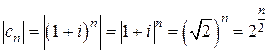 .
.
Применим формулу (5) для определения радиуса сходимости:
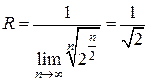 .
.
Значит, ряд сходится в круге 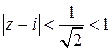 . Так как точка
. Так как точка 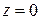 лежит вне этого круга, то ряд в точке
лежит вне этого круга, то ряд в точке 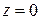 расходится. ☻
расходится. ☻
Задача 2. Показать, что область сходимости ряда 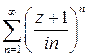 – вся комплексная плоскость.
– вся комплексная плоскость.
 2015-05-13
2015-05-13 2116
2116








