Введение........................................... 3
Основная часть...................................... 4
История возникновения геометрии.................. 4
Решение задач................................... 8
Заключение......................................... 24
Литература......................................... 25
5. Приложение........................................ 26
Введение.
Природа говорит языком математики: буквы этого языка – круги, треугольники и иные математические знаки.
Галилей.
Геометрия - одна из самых древних наук. Возникла геометрия в Египте более 4000 лет назад. В переводе с греческого слово «геометрия» означает «землемерие» («гео» - по-гречески земля, а «метрео» -мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений: людям нужно было определять расстояние между точками, площади участков и объемы тел (употребляемых, например, при постройке жилищ). Потребности жизни заставляли находить людей способы измерения площадей и объемов в разных странах и в разное время. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности людей и в начале своего развития служила преимущественно практическим целям. Это отразилось и в названиях многих геометрических фигур. Например, название фигуры трапеция происходит от греческого слова trapezion - «столик», от которого произошло также слово «трапеза» и другие родственные слова. Термин «линия» возник от латинского linum - «лён, льняная нить». В дальнейшем геометрия сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.
Цель моего реферата – рассмотреть решения некоторых практически важных задач, показать, как с помощью геометрических знаний определить, например, расстояние до недоступной точки или определить высоту предмета. При работе над этой темой я использовал различную литературу. Основным источником реферата является книга «Занимательная геометрия» Я.И. Перельмана. В книге автор хочет возбудить у читателя интерес к геометрии, или, говоря словами автора, «внушить охоту и воспитать вкус к её изучению – прямая задача настоящей книги».
Основная часть.
История возникновения геометрии.
Геометрия - одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках. Слово геометрия греческого происхождения. В буквальном смысле оно означает «землемерие». Оно составлено из двух древнегреческих слов gе -«Земля» и metreo- «измеряю».
Возникла геометрия в Египте более 4000 лет назад. Вот что пишет о зарождении геометрии греческий историк Геродот, живший около 2500 лет назад: «Сезострит, египетский царь, произвел деление земель, отмерив каждому египтянину, участок по жребию, сообразно этим участкам с их владельцев ежегодно взимал налоги.
|
|
Если Нил заливал чей-нибудь участок, то пострадавший обращался к царю и докладывал о случившимся. Тогда царь посылал землемеров (геометров), они измеряли, на сколько уменьшился участок и сообразно этому понижали налог. Вот откуда пришла геометрия и перешла из этой страны в Грецию».
Об этом же пишет и другой греческий ученый Евцем Родовский (4в до н.э.): «Геометрия была открыта египтянами и возникла при измерении земли. Это измерение было им необходимо вследствие разлива реки Нил, постоянно смывавшего границы. Нет ничего удивительного в том, что эта наука, как и другие, возникла из потребностей человека. Всякое возникающее знание из несовершенного состояния переходит в совершенное».
Нельзя думать, что не будь Нила с его мощными разливами – не было бы геометрии. Людям нужно было определять расстояние между точками, площади участков и объемы тел (употребляемых, например, при постройке жилищ) и они создали бы геометрию не в Египте, так в Индии, не и Индии, так в Китае. Да оно так и было. Потребности жизни заставляли находить людей способы измерения площадей и объемов в разных странах и в разное время.
|
|
В течение многих веков постепенно накапливали древние египтяне различные научные знания, в том числе знания по геометрии. Они сумели довольно точно определять площади фигур, объемы некоторых тел, решать некоторые другие геометрические задачи.
Но геометрии, как науки, у них не было. У них было много различных правил - рецептов, не соединенных между собой общей идеей, не приведенных в единую стройную систему. Этими рецептами владели чаще всего жрецы храмов, которые держали их в секрете.
Цари древнего Египта постоянно вели долгие изнурительные войны, которые ослабляли экономическую мощь страны. Были периоды, когда Египет завоевывался разными другими народами – это были периоды жестокой эксплуатации страны – наука и искусство пришли в упадок.
Но к северу от Египта, уже зародилось новое государство – Греция. Греческие купцы посещали Египет и, возвращаясь, много рассказывали об этой чудесной стране. Вместе с купцами Египет стали посещать ученые. И достижения египетской науки постепенно стали известны древним грекам.
Но Греки не просто усвоили достижения египтян. Они исправили их ошибки и развивали геометрию дальше. Именно в древней Греции около 2500 лет назад геометрия стала математической наукой.
В VII веке до н.э. центром математического творчества становится так называемая пифагорейская школа в южной Италии. Здесь были открыты несоизмеримые отрезки, создано учение о подобии, найдены способы построения некоторых правильных многоугольников и многогранников, доказана теорема Пифагора и т.д.
К 300-м годам до н.э. геометрия становится самостоятельной математической наукой. К этому времени древнегреческий ученый Евклид (III в. до н.э.) написал книгу, называемую им «Начала», написание которой относится к 325-300 годам до н.э.
Евклид собрал почти все, что было создано до него, по геометрии и привел в стройную единую систему. Он взял за основу некоторые положения, так называемые аксиомы (постулаты), и из них путем последовательных рассуждений сумел вывести все теоремы геометрии. Т.о., в этой книге Евклид подытожил накопленные к тому времени геометрические знания и попытался дать законченное аксиоматическое изложение этой науки. «Начала» Евклида более полутора тысяч лет переписывались от руки в Греции, Италии, Египте, Индии, Средней Азии и других странах. С возникновением книгопечатания «Начала» сотни раз перепечатывались на всех языках мира. Это одна из наиболее распространенных на земном шаре книг. Написана она была настолько хорошо, что в течение 2000 лет всюду преподавание геометрии велось либо по переводам, либо по незначительным переработкам книги Евклида. Например, таким пособием был учебник А.П. Киселева, по которому советская школа работала до середины ХХ столетия.
Продуманное и глубоко логическое изложение геометрии, данное в книге Евклида, привело к тому, что математики не мыслили возможности существования геометрии, отличной от евклидовой. Немецкий философ-идеалист XVIII в. И. Кант и многие его последователи считали, что понятия и идеи евклидовой геометрии (единственно возможной, чуть ли не божественной) были заложены в человеческое сознание еще до того, как человек научился что-либо осознавать.
Ученые, жившие после Евклида добавили к «Началам» несколько новых теорем, кое-что изменили, но основная масса материала, границы, определяющие ее объем и метод остались прежними. Поэтому геометрия, которую мы изучаем, называется Евклидовой.
Большой вклад в дальнейшее исследование различных вопросов геометрии внесли Архимед (ок. 287 -212 гг. до н. э.), Апполоний (III в. до н. э.) и другие древнегреческие учёные.
Качественно новый этап в развитии геометрии начался лишь много веков спустя – в XVII в. н. э. – и были связаны с накопленными к этому времени достижениями алгебры. Французский математик и философ Р. Декарт (1596 – 1650) предложил новый подход к решению геометрических задач: ввёл метод координат, связав геометрию и алгебру, что позволило решать многие геометрические задачи алгебраическими методами.
|
|
На Руси самое древнее сочинение по арифметике, сохранившееся до нас, написано в 1196 году новгородским монахом Кириком. Самое древнее сочинение, сохранившееся до наших дней и содержащее геометрические сведения, написано в начале XVII века (вероятно, в 1607 году), оно называлось «Устав ратных дел». В этом сочинении содержатся правила (рецепты) для решения задач на определение расстояния до предметов. Никаких теорем или доказательств верности не приводится.
В других рукописях («Книга и письма» и другие) даются правила изменения площадей, нахождения расстояний, определение объемов тел. В этих правилах много ошибок и совсем не приводится доказательств.
Распространению на Руси геометрических знаний препятствовала церковь. Попы боялись, что вместе с книгами с запада в Россию будет проникать католическая религия, поэтому вводили жестокие меры против тех, кто занимался математикой. В одном древнерусском поучении говорится: «богомерзостен перед богом всякий, кто любит геометрию».
В течение XVII века геометрические знания на Руси распространялись медленно.
В XVIII веке геометрия получила большое распространение. В России была открыты Академия наук, в Москве был открыт университет, во многих городах открывались школы и гимназии, появились учебники геометрии, как отечественные, так и переводные.
В конце XVIII в. у некоторых геометров возникла мысль о невозможности доказательства пятого постулата Евклида («И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых»), который из-за сложности формулировки обычно заменяют аксиомой параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Н. И. Лобачевский предпринял попытку доказать пятый постулат от противного, но не получил при этом противоречивых утверждений. В 1826 г. он сообщил об открытии новой геометрии, отличной от геометрии Евклида. Такая геометрия получила название геометрии Лобачевского. К аналогичным выводам пришёл венгерский математик Я. Бойяи и немецкий математик К. Ф. Гаусс.
Открытие новой геометрии оказало огромное влияние на развитие науки. Геометрия Лобачевского широко используется в естествознании. Неизмеримо влияние новой геометрии на развитие самой геометрии. Наиболее ярко оно выразилось в дальнейшем углублении наших представлений о пространстве: до Лобачевского казалось, что геометрией окружающего нас мира может быть только евклидова геометрия. Современной наукой установлено, что евклидова геометрия лишь приближённо, хотя и с большой точностью, описывает окружающее нас пространство, а в космических масштабах она имеет заметное отличие от геометрии реального пространства.
Бурное развитие математики в XIX в. привело к ряду замечательных открытий. Так, выдающимся немецким математиком Б. Риманом (1826 – 1866) была создана новая геометрия, обобщающая и геометрию Евклида, и геометрию Лобачевского.
В настоящее время геометрия широко используется в самых разнообразных разделах естествознания: в физике, химии, биологии и т. д. Неоценимо её значение в прикладных науках: в машиностроении, геодезии, картографии. Методы геометрии широко применяются практически во всех разделах науке и техники и, конечно же, в самой математике.
Решение задач.
Задача № 1.
Определение расстояния до недоступной точки.
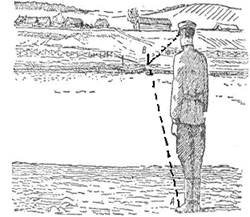
Дать геометрическое объяснение «способа козырька».
Этот способ часто применяется военными и туристами, для определения расстояния до недоступной точки.
Решение.
Луч зрения, касающийся обреза козырька (ладони, записной книжки), первоначально направлен на линию противоположного берега. Когда человек поворачивается, то луч зрения, подобно ножке циркуля, как бы описывает окружность, и тогда расстояние до предмета на том берегу равно расстоянию до предмета на этом берегу.
Задача № 2.
Определение высоты предмета.
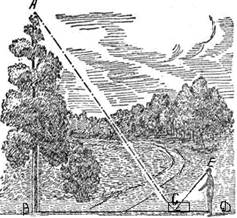
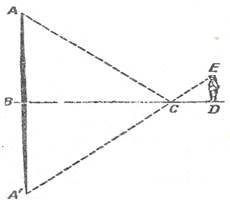
Вот своеобразный способ определения высоты дерева - при помощи зеркала. На некотором расстоянии от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку Д, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ЕД), во сколько раз расстояние ВС от зеркала до дерева больше расстояния СД от зеркала до наблюдателя. Почему?
Решение.
Способ основан на законе отражения света. Вершина А отражается в точке А' так, что АВ=А'В. Из подобия же треугольников ВСА' и СЕД следует, что АВ':ЕД=ВС:СД. В этой пропорции остается лишь заменить А'В равным ему АВ, чтобы обосновать указанное в задаче соотношение.
Этот удобный и нехлопотливый способ можно применять во всякую погоду, но не в густом насаждении, а к одиноко стоящему дереву.
Задача № 3.
Определение высоты предмета.
По способу Жюля Верна
Следующий – тоже весьма несложный – способ измерения предметов картинно описан у Жюля Верна в известном романе «Таинственный остров».
«-Сегодня нам надо измерить высоту площадки Далекого Вида, - сказал инженер.
-Вам понадобится для этого инструмент? - спросил Герберт.
- Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.
-Тебе знакомы зачатки геометрии? - спросил он Герберта, поднимаясь с земли.
-Да.
-Помнишь свойства подобных треугольников?
- Их сходственные стороны пропорциональны.
-Правильно. Так вот: сейчас я построю два подобных прямоугольных треугольника. У меньшего одним катетом будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч. У другого основания треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мой луч зрения, совпадающий с направлением гипотенузы первого треугольника.
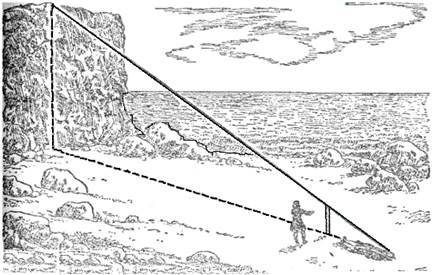
-Понял! - воскликнул юноша - Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены.
-Да. И следовательно, если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты».
Оба горизонтальных расстояния были измерены: меньшее - 15 футов, большее - 500 футов. По окончании измерений инженер составил следующую запись: 15:500=10:х, 500∙10=5000, 5000:15=333,3 Значит, высота гранитной стены равнялась 333 футам.
Задача № 4.
Определение величины угла.
Тень ВС от отвесного шеста АВ высотой 4,2 м имеет 6,5 м длины. Какова в этот момент высота Солнца над горизонтом, т. е. как велик угол С?
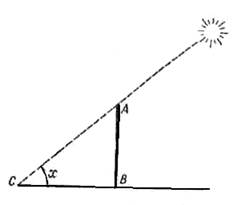
Решение
sin 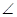 С =
С = 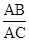
Но 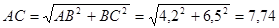
Поэтому sin 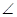 С =
С =  = 0,55.
= 0,55.
Соответствующий угол равен 33°. Высота Солнца равна 33° с точностью до 0,5.
Задача № 5.
Определение расстояния.
Бродя с компасом (буссолью) возле реки, вы заметили, на ней островок А и желаете определить его расстояние от точки В на берегу. Для этого вы определяете по компасу величину угла АВN, составленного с направлением север – юг (NS) прямой B А. Затем измеряете длину отрезка ВС и определяете величину угла NВС между ним и NS. Наконец, то же самое делаете в точке С для прямой СА. Допустим, что вы получили следующие данные:
направление ВА отклоняется от NS к востоку на 52°
направление ВС отклоняется от NS к востоку на110°
направление СА отклоняется от NS к востоку на 27°
Длина ВС =187 м.
Как по этим данным вычислить расстояние ВА?
Решение
В треугольнике АВС нам известна сторона ВС. Угол АВС=1100-520=580; угол АСВ=1800-1100-270=430
Проведем в этом треугольнике высоту BD.
Имеем: sin 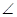 C = sin 430, значит sin
C = sin 430, значит sin 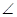 C =0,68. Но sin
C =0,68. Но sin 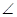 C =
C = 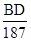 , значит,
, значит,
ВD= 187∙0,68=127.
Теперь в треугольнике АВD нам известен катетBD;

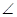 А =180°-(58°+43°) ==79° и
А =180°-(58°+43°) ==79° и 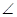 АВD == 90° -79° = 11°. Синус 11° мы можем вычислить: он равен 0,19. Следовательно,
АВD == 90° -79° = 11°. Синус 11° мы можем вычислить: он равен 0,19. Следовательно,  = 0,19. С другой стороны, по теореме Пифагора
= 0,19. С другой стороны, по теореме Пифагора
АВ2=BD2+AD2.
Подставляя 0,19АВ вместо AD, а вместо ВD число 127, имеем:
AB2=1272+(0.19AB)2,
откуда АВ ≈ 129.
Итак, искомое расстояние до острова около 129 м.
Задача № 6.
Вычисление синуса.
Рассмотрим, как можно вычислять стороны треугольника с точностью до 2% и углы с точностью до 1°, пользуясь одним лишь понятием синуса и не прибегая ни к таблицам, ни к формулам. Такая упрощенная тригонометрия может пригодиться во время загородной прогулки, когда таблиц под рукой нет, а формулы полузабыты. Робинзон на острове мог бы пользоваться такой тригонометрией. Что такое синус острого угла?
Синус острого угла прямоугольного треугольника — отношение противолежащего катета к гипотенузе в том треугольнике, который отсекается от угла перпендикуляром к одной из сторон.
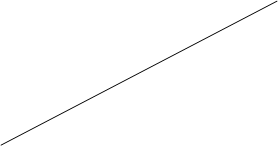 D'
D'
 B'
B'
 D
D


 В
В
 С
С

 А В Е Е' С' А С D
А В Е Е' С' А С D
Например, sin  А=
А=  =
=  =
= 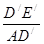 =
= 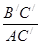 . Вследствие подобия образовавшихся здесь треугольников все эти отношения равны друг другу.
. Вследствие подобия образовавшихся здесь треугольников все эти отношения равны друг другу.
Чему же равны синусы различных углов от 1°до 90°? Как узнать это, не имея под рукой таблиц? Весьма просто: надо составить таблицу синусов самому.
Начнем с тех углов, синусы которых нам известны из геометрии. Это, прежде всего, угол в 90°, синус которого равен 1. Затем угол в 45°, синус которого легко вычислить по теореме Пифагора; он равен 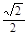 , т. е.0,707.
, т. е.0,707.
Далее нам известен синус 30°; так как катет, лежащий против такого угла, равен половине гипотенузы, то sin300= 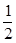
Итак, мы знаем синусы трех углов:
Sin900=1,
sin300=0,5,
sin450=0,707.
Этого, конечно, недостаточно для решения геометрических задач; необходимо знать синусы и всех промежуточных углов, по крайней мере, через каждый градус. Для очень малых углов можно при вычислении синуса вместо отношения катета к гипотенузе брать без большой погрешности отношение дуги к радиусу:

Из рис. видно, что отношение 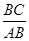 мало отличается от отношения
мало отличается от отношения 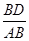 .Последние же легко вычислить. Например, для угла в 1 дуга BD=
.Последние же легко вычислить. Например, для угла в 1 дуга BD= 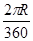 , где
, где 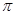 =3,14159… и, следовательно, sin1о можно принять равным
=3,14159… и, следовательно, sin1о можно принять равным 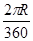 =
= 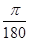 =0,0175. Таким же образом находим: sin2° =0,0349, sin3°= 0,0524, sin4°= 0,0698, sin 5° =0,0873.
=0,0175. Таким же образом находим: sin2° =0,0349, sin3°= 0,0524, sin4°= 0,0698, sin 5° =0,0873.
Но надо убедиться, как далеко можно продолжать эту табличку, не делая большой погрешности. Если бы мы вычислили по такому способу sin 30°, то получили бы 0,524 вместо 0,500: разница была бы уже во второй значащей цифре, и погрешность составляла бы  т. е. около 5%. Это чересчур грубо даже для нетребовательной походной тригонометрии. Чтобы найти границу, до которой позволительно вести вычисление синусов по указанному приближенному способу, постараемся найти точным приёмом sin15°. Для этого воспользуемся следующим построением. Пусть sin15о =
т. е. около 5%. Это чересчур грубо даже для нетребовательной походной тригонометрии. Чтобы найти границу, до которой позволительно вести вычисление синусов по указанному приближенному способу, постараемся найти точным приёмом sin15°. Для этого воспользуемся следующим построением. Пусть sin15о =  . Продолжим ВС на равное расстояние до точки D, соединим А с D, тогда получим два равных треугольника: АDС и AВС и угол BAD, равный 30°. Опустим на АD перпендикуляр ВЕ;
. Продолжим ВС на равное расстояние до точки D, соединим А с D, тогда получим два равных треугольника: АDС и AВС и угол BAD, равный 30°. Опустим на АD перпендикуляр ВЕ;
образуется прямоугольный треугольник ВАЕ с углом 30°
(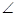 ВAE), тогда ВЕ=
ВAE), тогда ВЕ= 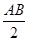 . Далее вычисляем АЕ из треугольника АВЕ по теореме Пифагора:
. Далее вычисляем АЕ из треугольника АВЕ по теореме Пифагора: 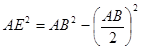 , АЕ2=
, АЕ2= 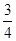 АВ2
АВ2
АЕ= 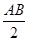
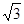 , АЕ=0,866АВ.
, АЕ=0,866АВ. 
Значит, ЕD=АD– АЕ=АB– 0,866 АВ = 0,134 АВ. Теперь из треугольника ВЕD вычисляем ВD:
ВD2=ВЕ2 + ЕD2,  BD2=0,268АВ2,
BD2=0,268АВ2,
BD= 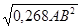 , BD =0,518AB.
, BD =0,518AB.
Половина ВD, т.е. ВС равна 0,259AB, следовательно, искомый синус
sin15°= 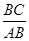 =
= 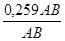 =0,259.
=0,259.
Это – табличное значение sin 15°, если ограничиться тремя знаками. Приближенное же значение его, которое мы нашли бы по прежнему способу, равно 0,262. Сопоставляя значения
0,259 и 0,262,
видим, что, ограничиваясь двумя значащими цифрами, мы получаем:
0,26 и 0,26,
т. е. тождественные результаты. Ошибка при замене более точного значения (0,259) приближенным (0,26) составляет
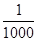 , т. е. около 0,4%. Это–погрешность, позволительная для походных расчетов, и, следовательно, синусы углов от 1 до 15° мы вправе вычислить по нашему приближенному способу.
, т. е. около 0,4%. Это–погрешность, позволительная для походных расчетов, и, следовательно, синусы углов от 1 до 15° мы вправе вычислить по нашему приближенному способу.
Для промежутка от 15 до 30° мы можем вычислять синусы при помощи пропорций. Будем рассуждать так. Разность между sin30° и sin15° равна 0,50—0,26=0,24. Значит, можем мы допустить, что при увеличении угла на каждый градус синус его возрастает примерно на 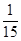 этой разности, т. е. на
этой разности, т. е. на 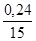 =0,016. Строго говоря, это, конечно, не так, но отступление от указанного правила обнаруживается только в третьей значащей цифре, которую мы все равно отбрасываем. Итак, прибавляя последовательно по 0,016 к sin15°, получим синусы 16, 17, 18° и т. д.:
=0,016. Строго говоря, это, конечно, не так, но отступление от указанного правила обнаруживается только в третьей значащей цифре, которую мы все равно отбрасываем. Итак, прибавляя последовательно по 0,016 к sin15°, получим синусы 16, 17, 18° и т. д.:
sin16o=0,26+0,016=0,28,
sin17o=0,26+0,032=0,29,
sin18о=0,26+0,048=0,31,
………………………….
Sin25о=0,26+0,16=0,42 и т. д.
Все эти синусы верны в первых двух десятичных знаках, т. е. с достаточной для наших целей точностью: они отличаются от истинных синусов менее чем на половину единицы последней цифры. Таким же способом поступают при вычислении синусов углов в промежутках между 30° и 45°. Разность sin45°— sin 30° = 0,707—0,5 = 0,207. Разделив ее на 15, имеем 0,014, Эту величину будем прибавлять последовательно к синусу 30°; тогда получим:
sin 31°=0,5 +0,014=0,51,
sin 32°=0,5+0,028=0,53,
sin 40°=0,5+0,14 =0,64 и т. д.
Остается найти синусы острых углов, больших 45°. В этом поможет нам теорема Пифагора. Пусть, например, мы желаем найти sin 53°, т. е. отношение 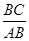 . Так как угол В равен 37°, то синус его мы можем вычислить по предыдущему: он равен 0,5+7Ч0,014=0,6. С другой стороны, мы знаем, что sin
. Так как угол В равен 37°, то синус его мы можем вычислить по предыдущему: он равен 0,5+7Ч0,014=0,6. С другой стороны, мы знаем, что sin 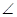 В=
В=  . Итак,
. Итак,  = 0,6, откуда AС= 0,6ЧАВ. Зная АС, легко вычислить ВС. Этот отрезок равен
= 0,6, откуда AС= 0,6ЧАВ. Зная АС, легко вычислить ВС. Этот отрезок равен  =
=  –АВ
–АВ 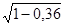 =0,8АВ. Расчет в общем нетруден, надо только уметь вычислять квадратные корни.
=0,8АВ. Расчет в общем нетруден, надо только уметь вычислять квадратные корни.
Задача № 7.
Указываемый в курсах алгебры способ извлечения квадратных корней легко забывается. Но можно обойтись и без него. В моих учебных книгах по геометрии приведен древний упрощенный способ вычисления квадратных корней при помощи деления. Здесь сообщу другой старинный способ, также более простой, нежели рассматриваемый в курсах алгебры.
Пусть надо вычислить 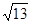 . Он заключается между 3 и 4
. Он заключается между 3 и 4
и, следовательно, равен 3 с дробью, которую обозначим через х.
Итак,
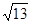 =3+х, откуда 13==9+6х+х2.
=3+х, откуда 13==9+6х+х2.
Квадрат дроби х есть малая дробь, которой в первом приближении можно пренебречь;
тогда имеем:
13= 9 + 6х. откуда 6х=4 и х = 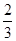 = 0,67.
= 0,67.
Значит, приближенно 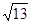 = 3,67. Если мы хотим определить значение корня еще точнее, напишем уравнение
= 3,67. Если мы хотим определить значение корня еще точнее, напишем уравнение 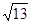 =3
=3 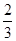 +у, где у – небольшая дробь положительная или отрицательная. Отсюда 13=
+у, где у – небольшая дробь положительная или отрицательная. Отсюда 13=  +
+  у+у2 . Отбросив у2, находим, что у приближенно равен –
у+у2 . Отбросив у2, находим, что у приближенно равен –  = –0,06. Следовательно во втором приближении
= –0,06. Следовательно во втором приближении 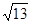 =3,67–0,06= 3,61. Третье приближение находим тем же приемом и т, д.
=3,67–0,06= 3,61. Третье приближение находим тем же приемом и т, д.
Обычным, указываемым в курсах алгебры способом мы нашли бы 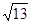 с точностью до 0,01 —также 3,61.
с точностью до 0,01 —также 3,61.
Задача № 8.
Найти угол по синусу.
Итак, мы имеем возможность вычислить синус любого угла от 0 до 90° с двумя десятичными знаками. Надобность в готовой таблице отпадает; для приближенных вычислений мы всегда можем сами составить ее, если пожелаем.
Но для решения тригонометрических задач нужно уметь выполнять и обратную операцию — вычислять углы по данному синусу. Это тоже несложно. Пусть требуется найти угол, синус которого равен 0,38. Так как данный синус меньше 0,5, то искомый угол меньше 30°. Но он больше 15°, потому что sin 15°, как мы знаем, равен 0,26. Чтобы найти этот угол, заключающийся в промежутке между 15° и 30°, поступаем, как объяснено выше.
0,38–0,26= 0,12.
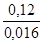 =7,5о
=7,5о
15о+7,5о=22,5о
Итак, искомый угол приближенно равен 22,5°.
Другой пример: найти угол, синус которого равен 0,62:
0,62–0,50=0,12,
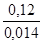 =8,6о
=8,6о
30о+8,6о=38,6о
Искомый угол приближенно равен 38,6°.
Наконец, третий пример: найти угол, синус которого равен 0,91.
Так как данный синус заключается между 0,71 и 1, то искомый угол лежит в промежутке между 45° и 90°. На рис. 3 ВС есть синус угла А. если ВА=1. Зная ВС, легко найти синус угла В:
АС2=1–ВС2=1–0,912=1–0,83=0,17,
АС= 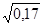 =0,42.
=0,42.
Теперь найдём величину угла В, синус которого равен 0,42; после этого легко будет найти угол А, равный 90о – В. Так как 0,42 заключается между 0,26 и 0,5,то угол В лежит в промежутке между 15о и 30о . Он определяется так:
0,42–0,26=0,16,
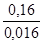 =10о
=10о
В=15о+10о=25о.
Значит 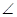 А=90о–25о=65о.
А=90о–25о=65о.
Теперь мы можем приближенно решать тригонометрические задачи, так как умеем находить синусы по углам и углы по синусам с точностью, достаточной для походных целей.
Задача № 9.
Определить ширину озера при помощи компаса.
Вычислить ширину АВ озера, если по компасу определено, что прямая СА уклоняется к западу на 21о, а СВ– к востоку на 22о, длинна СВ=68 м, СА=35 м.
Решение.
В треугольнике АВС нам известны угол 43о и длины заключающих его сторон –
68 м и 35м. Проводим высоту AD; имеем: sin 43о= 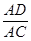 . Вычисляем, независимо от этого, sin 43о и получаем: 0,68. Значит,
. Вычисляем, независимо от этого, sin 43о и получаем: 0,68. Значит,  =0,68, AD=0,68×35=24. Затем вычисляем CD: СD2=АС2–АD2, СD2=352–242, СD2=649, СD=25,5;
=0,68, AD=0,68×35=24. Затем вычисляем CD: СD2=АС2–АD2, СD2=352–242, СD2=649, СD=25,5;
Теперь из треугольника АВD имеем:
АВ2=АD2+ВD2=242+42,52=3280;
АВ 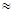 49
49
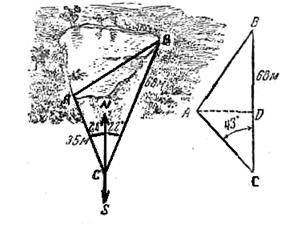
Итак, искомая ширина озера – около 49 м.
Если бы в треугольнике АВС нужно было вычислить и другие два угла, то, найдя, что АВ == 49, поступаем далее так:
sin  B=
B=  , sin
, sin  B=
B= 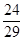 , sin
, sin 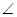 B=0.49, отсюда
B=0.49, отсюда 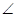 В=29о.
В=29о.
Третий угол А найдем, вычитая из 180° сумму углов 29° и 43°; он равен 108°.
Может случиться, что в рассматриваемом случае решения треугольника (по двум сторонам и углу между ними) данный угол не острый, а тупой. Если, например, в треугольнике АВС известны тупой угол А и две стороны, АВ и АС, то ход вычисления остальных его элементов таков. Опустив высоту BD, определяют ВD и АD из треугольника ВDА; затем, зная DА+АС, находят ВС и sin 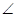 С, вычислив отношение
С, вычислив отношение 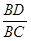 .
.
Задача № 10.
Треугольный участок.
Во время экскурсии мы измерили шагами стороны треугольного участка и нашли, что они равны 43, 60 и 54 шагам. Каковы углы этого треугольника?
В


43 54
 А D С
А D С
60
Решение.
Это — наиболее сложный случай решения треугольника: по трем сторонам. Однако и с ним можно справиться не обращаясь к другим функциям, кроме синуса. Опустив высоту ВD на длиннейшую сторону АС, имеем:
BD2=432–AD2, BD2=542–DC2,
откуда 432–AD2=542–DC2, DC2–AD2=542–432=1070.
Но DС2 – АD2 = (DС + АD) (DС – АD) =60 (DС – АD).
Следовательно, 60 (DС–АD) =1070 и DС–АD =17,8.
Из двух уравнений DС–АD=17,8 и DС+АD=60
получаем: 2DC=77,8, т. е. DС =38,9.
Теперь легко вычислить высоту:
ВD= 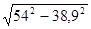 =37,4,
=37,4,
откуда находим:
sin 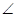 A =
A = 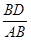 =
= 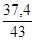 =0,87;
=0,87; 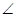 А около 60о
А около 60о
sin 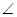 C =
C = 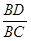 =
=  =0,69;
=0,69; 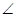 С около 44о
С около 44о
Третий угол 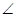 В = 180 — (
В = 180 — (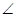 А +
А + 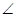 С) =76
С) =76 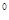
Если бы мы в данном случае вычисляли при помощи таблиц, по всем правилам «настоящей» тригонометрии, то получили бы углы, выраженные в градусах и минутах. Но эти минуты были бы заведомо ошибочны, так как стороны, измеренные шагами, заключают погрешность не менее 2—3%. Значит, чтобы не обманывать самого себя, следовало бы полученные «точные» величины углов округлить по крайней мере до целых градусов. И тогда у нас получился бы тот же самый результат, к которому мы пришли, прибегнув к упрощенным приемам. Польза нашей «походной» тригонометрии выступает здесь очень наглядно.
Задача № 11.
Выпрямление окружности.
Для многих практических целей достаточно взять для π;
число З 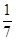 и выпрямить окружность, отложив ее диаметр на какой-либо прямой З
и выпрямить окружность, отложив ее диаметр на какой-либо прямой З 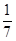 раза (деление отрезка на семь равных частей можно выполнить, как известно, вполне точно). Существуют и другие приближенные способы выпрямления окружности, применяемые на практике при ремесленных работах столярами, жестянщиками и т. п. Рассмотрим один способ выпрямления, дающий результат с чрезвычайно большой точностью.
раза (деление отрезка на семь равных частей можно выполнить, как известно, вполне точно). Существуют и другие приближенные способы выпрямления окружности, применяемые на практике при ремесленных работах столярами, жестянщиками и т. п. Рассмотрим один способ выпрямления, дающий результат с чрезвычайно большой точностью.
Если нужно выпрямить окружность О радиуса r, то проводят диаметр АВ а в точке В–перпендикулярную к ней прямую СD. Из центра О под углом 30° к АВ проводят прямую ОС. Затем на прямой СD от точки С откладывают три радиуса данной окружности и соединяют полученную точку D с А: длина отрезка АD равна длине полуокружности. Если отрезок АD удлинить вдвое, то приближенно получится выпрямленная окружность О. Ошибка менее 0,0002r.На чем основано это построение?
Решение.

По теореме Пифагора
СВ2+ОВ2=ОС2
Обозначив радиус 0В через r и имея в виду, что СВ= 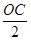
(как катет, лежащий против утла в 30о), получаем:
СВ2+ r 2=4СВ2,
СВ= 
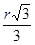 .
.
Далее, в треугольнике АВD
ВD=СD–СВ=3r– 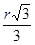 .
.
АD= 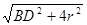 =
= 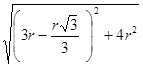 =
= 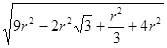 =3,14153r.
=3,14153r.
Сравнив этот результат с тем, который получается, если взять 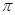 с большой степенью точности (
с большой степенью точности ( =3,141593), мы видим, что разница составляет всего 0,00006r. Если бы мы по этому способу выпрямляли окружность радиусом в 1 м, ошибка составляла бы для полуокружности всего 0,00006 м, а для полной окружности—0,00012 м, или 0,12 мм.
=3,141593), мы видим, что разница составляет всего 0,00006r. Если бы мы по этому способу выпрямляли окружность радиусом в 1 м, ошибка составляла бы для полуокружности всего 0,00006 м, а для полной окружности—0,00012 м, или 0,12 мм.
Задача № 12.
Треугольник с наибольшей площадью.
Какую форму нужно придать треугольнику, чтобы при данной сумме его сторон он имел наибольшую площадь? Мы заметили раньше, что этим свойством обладает равносторонний треугольник. Но как это доказать?
Решение.
Площадь S треугольника со сторонами а, b, с и периметром а+b+c=2р выражается, как известно из курса геометрии, так:
S = 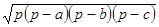 ,
,
откуда
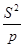 =
= 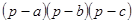 .
.
Площадь S треугольника будет наибольшей тогда же, когда станет наибольшей величиной и ее квадрат S2, или выражение  , где p, полупериметр, есть согласно условию величина неизменная. Но так как обе части равенства получают наибольшее значение одновременно, то вопрос сводится к тому, при каком условии произведение
, где p, полупериметр, есть согласно условию величина неизменная. Но так как обе части равенства получают наибольшее значение одновременно, то вопрос сводится к тому, при каком условии произведение  становится наибольшим. Заметив, что сумма этих трех множителей есть величина постоянная,
становится наибольшим. Заметив, что сумма этих трех множителей есть величина постоянная,
p–a + p – b + p – c = 3p – (a + b + c) = 3p – 2p = p,
мы заключаем, что произведение их достигнет наибольшей величины тогда, когда множители станут равны, т. е. когда осуществится равенство
р–а = р – b = р – с,
откуда а = b = с.
Итак, треугольник имеет при данном периметре наибольшую площадь тогда, когда стороны его равны между собой.
Задача № 13.
Задача Наполеона.
Одно из 7 древних чудес света – египетские пирамиды. Самая знаменитая из них – пирамида Хеопса высотой 147 м., в основании которой квадрат со стороной 233 м. Если из каменных блоков пирамиды возвести стену толщиной 20 см вокруг Франции, то какова будет высота этой стены? (Общая длина морских и сухопутных границ Франции 5000 км, формула для вычисления объёма прямоугольного параллелепипеда: 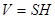 , где S – площадь основания параллелепипеда, H – его высота, формула для вычисления объёма пирамиды:
, где S – площадь основания параллелепипеда, H – его высота, формула для вычисления объёма пирамиды: 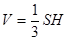 , где S – площадь основания пирамиды, H – её высота.)
, где S – площадь основания пирамиды, H – её высота.)
Решение.
Объём пирамиды 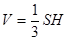 ,
, 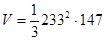 ,
, 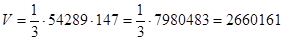 (м3)
(м3)
Объём прямоугольного параллелепипеда 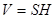 ,
, 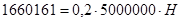 ,
, 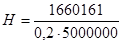 , H=2,660161(м) или Н≈266 см. Итак, вокруг Франции можно возвести стену толщиной 20 см высотой примерно 266 см.
, H=2,660161(м) или Н≈266 см. Итак, вокруг Франции можно возвести стену толщиной 20 см высотой примерно 266 см.
Задача № 14.
Задача о скорости.
Друзья поехали на рыбалку на велосипедах. Озеро, которое они облюбовали, находится в 9 км от ближайшей точки шоссе. Село расположено в 12 км по шоссе от этой точки. Туда ребята поехали напрямик к озеру, а обратно – сначала перпендикулярно к шоссе, а затем по шоссе. Скорость по бездорожью 8 км/ч. При какой скорости на шоссе обратный путь выгоднее по времени?
Решение.
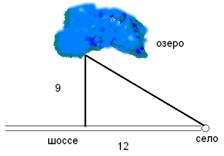
Путь друзей образует прямоугольный треугольник, у которого известны катеты (дорога от шоссе до озера и дорога от этой точки шоссе до села). По теореме Пифагора найдём гипотенузу (дорога напрямую от села до озера) данного прямоугольного треугольника: 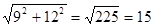 . Итак, расстояние от села до озера равно 15 км. Так как скорость по бездорожью равна 8 км/ч, то на путь к озеру ребята потратили время
. Итак, расстояние от села до озера равно 15 км. Так как скорость по бездорожью равна 8 км/ч, то на путь к озеру ребята потратили время 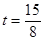 ч, t=1
ч, t=1  ч, а на путь от озера до шоссе
ч, а на путь от озера до шоссе 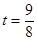 ч, t=1
ч, t=1 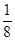 ч. Обратный путь выгоднее по времени, если выполняется неравенство:
ч. Обратный путь выгоднее по времени, если выполняется неравенство: 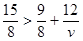 , где
, где 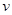 – скорость по шоссе,
– скорость по шоссе, 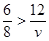 ,
, 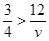 ,
, 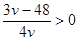 . Так как
. Так как 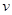 по условию задачи число положительное, то
по условию задачи число положительное, то 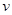 >16. Значит, чтобы обратный путь был выгоднее по времени, друзья должны ехать со скоростью, большей 16 км/ч.
>16. Значит, чтобы обратный путь был выгоднее по времени, друзья должны ехать со скоростью, большей 16 км/ч.
Задача № 15.
Измерение глубины реки.
Как измерить глубину реки, оставаясь на берегу реки? Известен такой способ. К грузилу привязывают две бечевки разной длины (пусть b и c), а на их концы поплавки. Всю эту конструкцию бросают в воду. Затем измеряют расстояние между поплавками (пусть оно равно a), когда их отнесёт течением. Как найти глубину h?
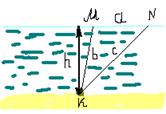
Решение.
Рассмотрим 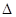 МNК. S
МNК. S 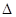 МNК=
МNК= 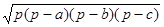 , где
, где 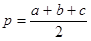 . С другой стороны, S
. С другой стороны, S 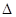 МNК=
МNК= 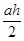 . Тогда получим, что
. Тогда получим, что 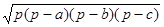 =
= 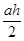 , значит,
, значит, 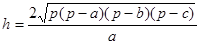 .
.
Заключение.
Возникновение геометрических знаний связано с практической деятельностью людей. Еще в древности геометрия превратилась в дедуктивную, строго логическую науку, построенную на основе системы аксиом. Она непрерывно развивалась, обогащалась новыми теоремами, методами. Интересы геометров и направления их научных исследований порою менялись в процессе исторического развития этой науки, поэтому нелегко дать точное и исчерпывающее определение, что такое геометрия сегодня, каков ее предмет, содержание и методы.
В книге «Диалектика природы» Ф.Энгельс определил геометрию как науку о пространственных формах окружающего нас реального мира, т.е. как часть математики, изучающую свойства пространства. Это философское определение полностью отражало состояние геометрии в то время, когда жил и работал Ф. Энгельс. Но в наше время возникли и оформились новые важные отделы геометрии. Каждый из этих разделов имеет свою специфику, которая уже не всегда укладывается в определение геометрии, данное в прошлом веке Ф. Энгельсом. Крупный советский геометр, академик А.Д. Александров, которому принадлежат работы, не только по геометрии, но и в области философии математики, расширил рамки энгельсовского определения, сказав, что геометрия изучает пространственные и пространственноподобные формы и отношения реального мира.
В учебнике геометрии имеется много задач, но практических мало. В своём реферате я рассмотрел наиболее часто встречающиеся практические задачи и способы применения теоретических знаний, например, как определить расстояние до недоступной точки, высоту предмета и некоторые другие. Таким образом, я постарался показать огромное практическое значение геометрии, так как трудно указать те отрасли народного хозяйства и науки куда бы не проникла геометрия. Без участия геометрии немыслимо было бы освоение космоса. Геометрия необходима и инженеру, и архитектуру, и колхознику. Изучение законов природы немыслимо без знаний математики. Не случайно известный итальянский физик и математик Галилей сказал так: «Природа говорит языком математики, буквы этого языка - круги, треугольники и иные математические знаки».
4. Литература:
1. Перельман Я. И. Занимательная алгебра. Занимательная геометрия. – М.: ООО «Издательство АСТ», 2002.
2. Готман Э. Г., Скопец З. А. Задача одна – решения разные: Геометрические задачи. – М.: Просвещение, 2000.
3. Фоминых Ю. Ф. Прикладные задачи по алгебре для 7-9 классов. – М.: Просвещение, 1999.
4. Зив Б. Г., Мейлер В. М., Баханский А. Г. Задачи по геометрии: Пособие для учащихся 7 – 11 кл. общеобразовательных учреждений. – М.: Просвещение, 2000.
5. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия, 7 – 9: Учебник для общеобразовательных учреждений. – М.: Просвещение, 2002.
6. Энциклопедический словарь юного математика./Составитель Савин А. П. – М.: Педагогика, 1989.
 2020-01-15
2020-01-15 22435
22435

