2015-05-18
10474Пример № 1. Анализируется прибыль предприятия Y (млн. ден. ед.) в зависимости от расходов на рекламу X (млн. ден. ед.). По наблюдениям за 9 лет получены следующие данные:
| yi | 5,0 | 7,0 | 13,0 | 15,0 | 20,0 | 25,0 | 22,0 | 20,0 | 17,0 |
| хi | 0,8 | 1,0 | 1,8 | 2,5 | 4,0 | 5,7 | 4,3 | 5,3 | 3,9 |
1. Построить корреляционное поле. Выдвинуть предположение о характере статистической зависимости между переменными X и Y.
2. Найти параметры линейного уравнения регрессии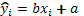 
. Поясните экономический смысл выборочного коэффициента регрессии.
3. Найти коэффициент парной корреляции и оценить тесноту связи на основе таблицы Чеддока.
4. Найти коэффициент детерминации R 2.
5. Оценить статистическую значимость уравнения регрессии на уровне 0,05, используя F- статистику.
6. Полученное уравнение регрессии изобразить графически. Сделать вывод о качестве построенной модели.
7. Вычислить прогнозное значение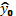 
при прогнозном значении x 0, составляющем 130% от среднего уровня x.
Решение:
1. Построим корреляционное поле:
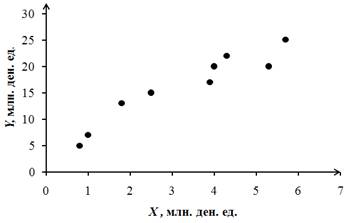
Анализ рисунка позволяет сделать предположение о наличии сильной линейной зависимости прибыли предприятия Y от расходов на рекламу X. При этом связь имеет положительную тенденцию, т.е. с увеличением расходов на рекламу увеличивается прибыль предприятия.
|
|
|
2. Найдем параметры линейного уравнения регрессии по формулам:
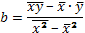
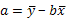
Рассчитаем сначала средние значения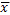 
, 
, 
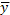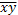и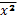 
.
| № | yi | хi | хi yi | yi 2 | хi 2 |
| 5,0 | 0,8 | 4,0 | 25,0 | 0,6 | |
| 7,0 | 1,0 | 7,0 | 49,0 | 1,0 | |
| 13,0 | 1,8 | 23,4 | 169,0 | 3,2 | |
| 15,0 | 2,5 | 37,5 | 225,0 | 6,3 | |
| 17,0 | 3,9 | 66,3 | 289,0 | 15,2 | |
| 20,0 | 4.0 | 80,0 | 400,0 | 16,0 | |
| 20,0 | 5,3 | 106,0 | 400,0 | 28,1 | |
| 22,0 | 4,3 | 94,6 | 484,0 | 18,5 | |
| 25,0 | 5,7 | 142,5 | 625,0 | 32,5 | |
| Сумма | 29,3 | 561,3 | 2666,0 | 121,4 | |
| Среднее | 3,26 | 62,37 | 296,22 | 13,49 |
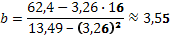
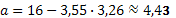млн. ден. ед.
Таким образом, уравнение регрессии:
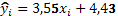
Выборочный коэффициент регрессии b показывает, что при увеличении расходов на рекламу на 1 млн. ден. ед. прибыль предприятия в среднем увеличивается на 3,55 млн. ден. ед.
3. Найдем коэффициент парной корреляции по формуле:
.
.
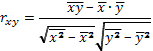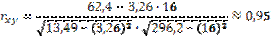Таким образом, линейная связь между переменными X и Y прямая, очень сильная.
4. Коэффициент детерминации:
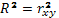
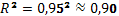
Таким образом, изменение прибыли предприятия Y на 90% обусловлено изменением расходов на рекламу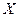 
и на 10% – действием других неучтенных в модели факторов.
5. Оценим статистическую значимость уравнения регрессии, используя F- статистику с 95% надежностью.
С помощью критерия Фишера проверяется нулевая гипотеза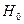 
о статистической незначимости уравнения регрессии. Конкурирующая гипотеза – уравнение регрессии статистически значимо.
Наблюдаемое значение критерия Фишера вычисляется по формуле:
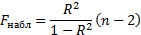
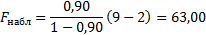
Найдем табличное значение критерия Фишера,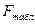 
определяется из специальной таблицы (см. приложение 2) с помощью трех чисел: уровня значимости 
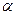и степеней свободы 
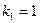и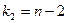 
:
|
|
|
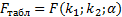
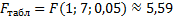
Видно, что наблюдаемое значение критерия Фишера превосходит табличное. Таким образом, нулевая гипотеза о статистической незначимости уравнения регрессии отклоняется на уровне 0,05 и принимается конкурирующая гипотеза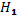 
, т.е. признается статистическая значимость уравнения регрессии.
6. Построим линейное уравнение регрессии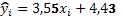 
.
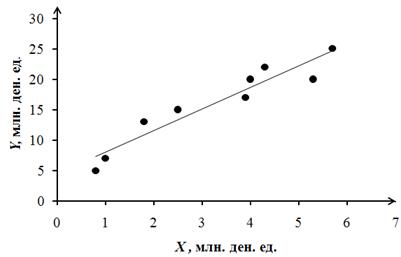
Можно сделать вывод о правомочности применения линейной регрессионной модели. Таким образом, полученное уравнение регрессии может быть использовано при прогнозировании.
7. Вычислим прогнозное значение 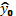при прогнозном значении x 0, составляющем 130% от среднего уровня x:
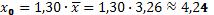млн. ден. ед.
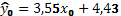
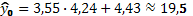млн. ден. ед.
Пример № 2. Зависимость спроса на товар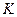 
от его цены характеризуется по 20 наблюдениям уравнением: 
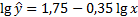. Доля остаточной дисперсии в общей составило 18 %.
1. Запишите данное уравнение в виде степенной функции. 2. Определите индекс корреляции. 3. Оцените значимость уравнения регрессии через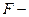 
критерий (
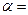0,05). Сделайте выводы.
Решение:
1. Преобразуем исходное уравнение к степенному виду:
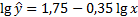
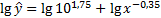
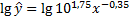
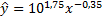
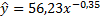
2. Найдем индекс корреляции:
.
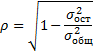
3. Проверим статистическую значимость уравнения регрессии с помощью критерия Фишера на уровне значимости 0,05. Индекс корреляции равен 0,91, тогда индекс детерминации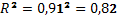 
.
Проверяется нулевая гипотеза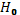 
об отсутствии нелинейной связи между переменными X и Y, т.е. 
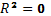, конкурирующая гипотеза 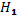о наличии нелинейной связи между переменными X и Y, т.е. 
.
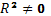Рассчитаем наблюдаемое значение критерия Фишера:
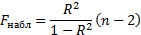
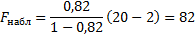
Находим табличное значение критерия Фишера:
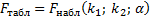
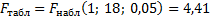
Сравним наблюдаемое и табличное значение критерия
Фишера:
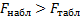
Таким образом, нулевая гипотеза об отсутствии связи между переменными X и Y отклоняется на уровне значимости 0,05 и принимается конкурирующая гипотеза 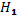, т.е. признается статистическая значимость уравнения регрессии.
Пример № 3. Для изучения рынка жилья в городе по данным о 21 коттедже было построено уравнение множественной регрессии:
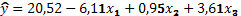
Стандартные ошибки параметров уравнения регрессии: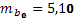 
, 
, 
, 
.
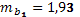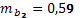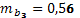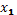– расстояние до центра города, км; 
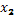– полезная площадь объекта, м2; 
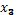– число этажей в доме, ед.
Множественный коэффициент детерминации: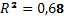 
.
Найдите скорректированный коэффициент детерминации. Оцените статистическую значимость параметров уравнения регрессии с помощью критерия Стьюдента на уровне 0,01.
Решение:
1. Найдем скорректированный коэффициент детерминации:
.
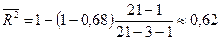2. Оцените статистическую значимость параметров уравнения регрессии с помощью критерия Стьюдента на уровне 0,01.
Проверяется нулевая гипотеза 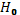о статистической незначимости, т. е. случайной природе параметров уравнения регрессии, конкурирующая гипотеза 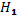о неслучайности параметров уравнения регрессии.
Рассчитаем наблюдаемые значения критерия Стьюдента:
, 
, 
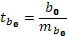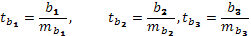
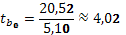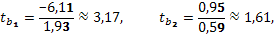
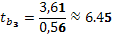
Найдем табличное значение критерия Стьюдента (см. приложение 4):
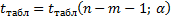
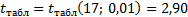
Сравним табличное значение критерия Стьюдента с наблюдаемыми значениями. Делаем вывод о статистической значимости параметров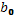 
, 
, 
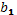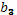. Параметр 
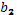статистически незначим, поэтому переменную 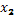необходимо исключить из уравнения регрессии.
Пример № 4. В результате исследования зависимости среднедневной заработной платы Y от среднедушевого прожиточного минимуме в день одного трудоспособного Х по n территориям региона было получено линейное уравнение регрессии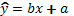 
. Исследуйте остатки данного уравнения регрессии на гетероскедастичность с помощью теста Голдфельда-Квандта на уровне значимости 0,05, если остаточные суммы квадратов для первой и второй групп соответственно равны 
и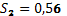 
; число степеней свободы остаточных сумм квадратов равны 
.
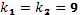Решение:
Проверяется нулевая гипотеза 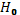об отсутствии гетероскедастичности остатков.
|
|
|
Конкурирующая гипотеза 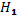– наличие гетероскедастичности остатков.
Наблюдаемое значение критерия Фишера находим по формуле:
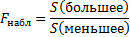
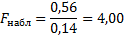
Находим табличное значение критерия Фишера:
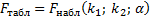
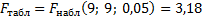
Сравним наблюдаемое и табличное значение критерия Фишера:
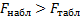
Таким образом, нулевая гипотеза об отсутствии гетероскедастичности остатков отклоняется на уровне значимости 0,05 и принимается конкурирующая гипотеза 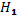, т.е. признается гетероскедастичность остатков.
Пример 5. Для линейного уравнения регрессии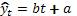 
исследуйте остатки на наличие автокорреляции на уровне значимости 0,01, используя тест Дарбина-Уотсона, если известны значения 
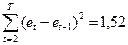и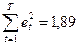 
; число наблюдений равно 20.
Решение:
Проверяется нулевая гипотеза 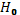об отсутствии автокорреляция. Конкурирующие гипотезы – 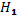и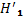 
соответственно о наличии положительной и отрицательной автокорреляции в остатках.
Рассчитаем критерий Дарбина-Уотсона по формуле:
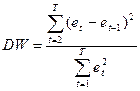
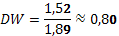
По таблице критических точек Дарбина Уотсона определим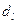 
(нижнее) и 
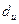(верхнее) значения критерия Дарбина-Уотсона для заданного числа наблюдений 
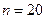, числа независимых переменных модели 
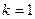и уровня значимости 0,01: 
; 
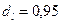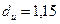(см. приложение 3).
По этим значениям числовой промежуток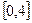 
разобьем на пять отрезков. Вывод о наличии (или отсутствии автокорреляции) делается по правилу:
a. если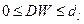 
, то существует положительная автокорреляция; гипотеза 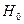отклоняется и с вероятностью 
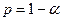принимается гипотеза 
;
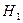b. если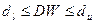 
, то попадаем в так называемую зону неопределенности и не имеем возможности ни опровергнуть, ни принять ни одну из гипотез.
c. если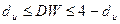 
, то нет оснований отклонить нулевую гипотезу: автокорреляция остатков отсутствует;
d. если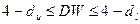 
, то попадаем в так называемую зону неопределенности и не имеем возможности ни опровергнуть, ни принять ни одну из гипотез.
e. если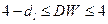 
, то существует отрицательная автокорреляция: гипотеза 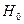отклоняется и с вероятностью 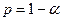принимается гипотеза 
.
,
,
,
,
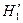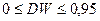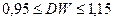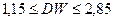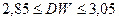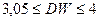
Найденное значение критерия Дарбина-Уотсона попадает в первый интервал (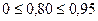
). Таким образом, можно сделать вывод о наличии положительной автокорреляции на уровне значимости 0,01.
|
|
|
Пример № 6. В результате анализа динамики объема продаж продукции торгового предприятия за 2000-2013 гг. было выявлено, что модель временного ряда имеет только трендовую составляющую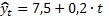 
млн. руб. (где t = 1, 2, …, 14). Сделайте точечный и интервальный прогноз объема продаж продукции предприятия в момент 
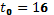(т.е. на 2015 г.), если уровень значимости равен 0,05, остаточная сумма квадратов 
.
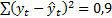Решение:
Точечный прогноз:
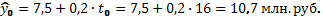
Предельная ошибка прогноза:
= 
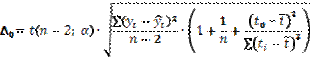
7,5.
Табличное значение критерия Стьюдента: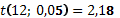 
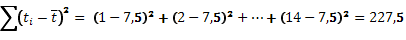
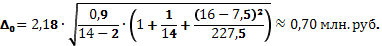
Интервальный прогноз:
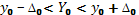
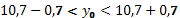
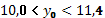
Таким образом, с вероятностью 0,95 можно утверждать, что в 2015 г. объем продаж продукции будет в диапазоне от 10,0 до 11,4 млн. руб.
Пример № 7. Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений модели мультипликатора-акселератора:
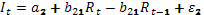
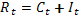
где C – расходы на потребление;
R – доход;
I – инвестиции;
t – текущий период;
t -1 – предыдущий период.
Решение:
Модель включает три эндогенные переменные (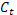
, 
, 
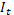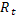) и две предопределенные переменные (две лаговые эндогенные переменные 
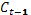и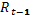 
).
Проверим необходимое условие идентификации для каждого уравнения модели.
Необходимое условие идентификации (НУИ):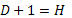 
– уравнение идентифицируемо; 
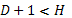– уравнение неидентифицируемо; 
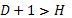– уравнение сверхидентифицируемо.
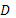– число предопределенных переменных, отсутствующих в анализируемом (рассматриваемом) уравнении, но присутствующих в системе; 
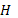– число эндогенных переменных, которые присутствуют в рассматриваемом уравнении. Предопределенные переменные – это экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные.
Первое уравнение. Уравнение включает в себя две эндогенные переменные (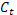 и 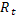) и не включает одну предопределенную переменную (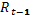). Таким образом, 1+1=2, т.е. уравнение идентифицируемо.
Второе уравнение. Уравнение включает в себя две эндогенные переменные (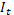 и 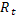) и не включает одну предопределенную переменную (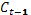). Таким образом, 1+1=2, т.е. уравнение идентифицируемо.
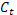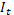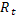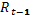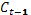Третье уравнение. Уравнение включает в себя три эндогенные переменные (, и ) и не включает две предопределенных переменных ( и ). Таким образом, 2+1=3, т.е. уравнение идентифицируемо.
Проверим теперь достаточное условие идентификации для каждого уравнения модели.
Достаточное условие идентификации (ДУИ):
Определитель матрицы, составленный из коэффициентов, отсутствующих в исследуемом уравнении, не равен 0, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы:
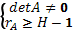(1)
Составим матрицу коэффициентов при переменных рассматриваемой модели:
|
|
|
|
|
| |
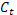
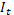
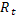
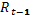
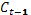
| Первое уравнение | -1 |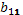 
| 
| ||
| Второе уравнение | -1 |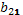 
|
| ||
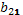
| Третье уравнение | -1 |
Первое уравнение. Матрица при переменных, которые не входят в уравнение, имеет вид:
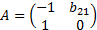
Определитель данной матрицы не равен нулю:
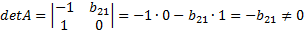
Ранг матрица A равен двум, поскольку определитель квадратной матрицы A не равен нулю. Тогда 2 > 2 - 1, т.е. выполняется второе неравенство системы (1). Таким образом, достаточное условие идентификации для первого уравнения выполняется.
Второе уравнение. Матрица при переменных, которые не входят в уравнение, имеет вид:
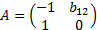
Определитель данной матрицы не равен нулю:
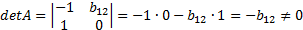
Ранг матрица A равен двум, поскольку определитель квадратной матрицы A не равен нулю. Тогда 2 > 2 - 1, т.е. выполняется второе неравенство системы (1). Таким образом, достаточное условие идентификации для второго уравнения выполняется.
Третье уравнение. Матрица при переменных, которые не входят в уравнение, имеет вид:
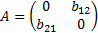
Определитель данной матрицы не равен нулю:
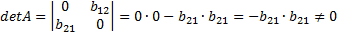
Ранг матрица A равен двум, поскольку определитель квадратной матрицы A не равен нулю. Тогда 2 = 3 - 1, т.е. выполняется второе неравенство системы (1). Таким образом, достаточное условие идентификации для третьего уравнения выполняется.
Таким образом, исследуемая система идентифицируема.
