ФР НСВ является ее исчерпывающей вероятностной характеристикой. Но она имеет недостаток, заключающийся в том, что по ней трудно судить о характере распределения СВ в небольшой окрестности той или иной точки числовой оси. Более наглядное представление дает функция 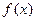 , которую называют плотностью распределения или плотностью вероятности.
, которую называют плотностью распределения или плотностью вероятности.
Пусть имеется НСВ  с ФР
с ФР 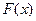 . Вычислим вероятность попадания этой СВ на элементарный участок
. Вычислим вероятность попадания этой СВ на элементарный участок 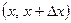 . Согласно формуле (3) имеем:
. Согласно формуле (3) имеем:
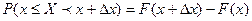 .
.
Составим отношение этой вероятности к длине участка 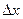 :
:
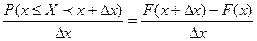 . (5)
. (5)
Соотношение (5) называют средней вероятностью, которая приходится на единицу длины этого участка.
Считая ФР 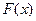 дифференцируемой, перейдем в равенстве (5) к пределу при
дифференцируемой, перейдем в равенстве (5) к пределу при 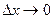 . Тогда получим:
. Тогда получим:
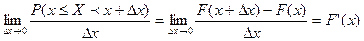 (6)
(6)
Опр. Плотностью распределения вероятностей НСВ  называют функцию
называют функцию 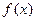 - первую производную от функции распределения
- первую производную от функции распределения 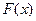 :
:
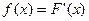 . ·
. ·
Смысл плотности распределения (ПР) состоит в том, что она указывает на то, как часто появляется СВ  в некоторой окрестности точки
в некоторой окрестности точки  при повторении опытов.
при повторении опытов.
Свойства плотности распределения.
1. Плотность распределения – неотрицательная функция: 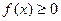 .
.
► Это непосредственно вытекает из того, что ПР 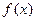 есть производная от неубывающей ФР
есть производная от неубывающей ФР 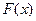 . ◄
. ◄
2. ФР СВ равна интегралу от ПР в интервале от -¥ до  :
:
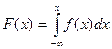 . (7)
. (7)
► По определению дифференциала функции имеем: 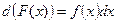 .
.
Следовательно,
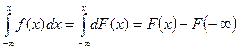 ,
,
но 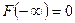 , поэтому верно (7). ◄
, поэтому верно (7). ◄
3. Вероятность того, что НСВ  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 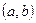 , равна определенному интегралу от плотности распределения, взятому в пределах от
, равна определенному интегралу от плотности распределения, взятому в пределах от 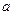 до
до 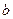 :
:
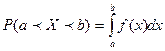 . (8)
. (8)
Геометрически полученный результат можно истолковать так: вероятность того, что НСВ примет значение, принадлежащее интервалу 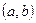 , равна площади криволинейной трапеции, ограниченной осью
, равна площади криволинейной трапеции, ограниченной осью 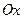 , кривой распределения
, кривой распределения 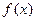 и прямыми
и прямыми 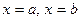 .
.
4. Интеграл в бесконечных пределах от плотности распределения равен единице:
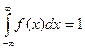 .
.
► Заменяя в равенстве (7) величину  на
на 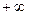 и учитывая, что
и учитывая, что 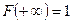 , получим:
, получим:
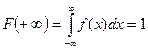 . ◄
. ◄
Нахождение функции распределения по плотности распределения.
Пусть 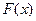 - вероятность того, что СВ примет значение, меньшее
- вероятность того, что СВ примет значение, меньшее  , т.е.
, т.е.
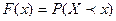 .
.
Т.к. неравенство 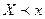 можно записать в виде двойного неравенства
можно записать в виде двойного неравенства 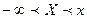 , то
, то
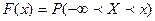 . (*)
. (*)
Полагая в формуле (*) 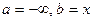 , имеем
, имеем
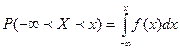 .
.
Окончательно получаем
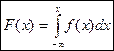 . (1)
. (1)
Например: Найти функцию распределения по данной плотности распределения. Построить график найденной функции.
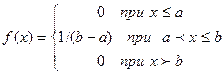 .
.
§ Воспользуемся формулой (1).
Если 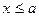 , то
, то 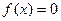 , Þ
, Þ 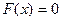 .
.
Если 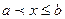 , то
, то 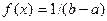 , Þ
, Þ
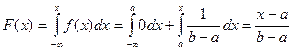 .
.
Если 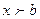 , то
, то
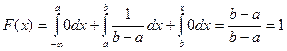 .
.
Искомая функция распределения
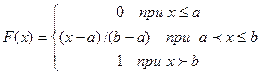 .
.
График этой функции изображен на рисунке.




 1
1
 |
0 
 §
§
 2015-06-10
2015-06-10 3088
3088
