Локальная теорема Лапласа

Выше была выведена формула Бернулли, позволяющая вычислить вероятность того, что событие появится в п испытаниях ровно k раз. При выводе мы предполагали, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях п достаточно трудно, так как формула требует выполнения действий над громадными числами.

Например, если n=50, k=30, р=0,1, то для отыскания вероятности Р₅₀(30) надо вычислить выражение

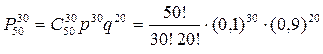
где 50! = 30 414 093 • 10⁵⁷, 30! = 26 525 286 • 10²⁵, 20! = 24 329 020 • 10¹¹. Есть возможность несколько упростить вычисления, пользуясь специальными таблицами логарифмов факториалов. Однако и этот путь остается громоздким и к тому же имеет существенный недостаток: таблицы содержат приближенные значения логарифмов, поэтому в процессе вычислений накапливаются погрешности; в итоге окончательный результат может значительно отличаться от истинного.

Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Локальная теорема Лапласа и дает асимптотическую[1] формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико.

Заметим, что для частного случая, а именно для р=1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра-Лапласа.

Доказательство локальной теоремы Лапласа довольно сложно, поэтому мы приведем лишь формулировку теоремы и примеры, иллюстрирующие ее использование.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р _n(k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции

,

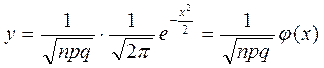при x = (k-np) / √npq.

Имеются таблицы, в которых помещены значения функции 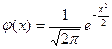, соответствующие положительным значениям аргумента х (см. приложение 1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция φ(х) четна, т. е. φ(–х) = – φ(х).

Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна

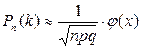, где x = (k-np) / √npq.

Пример 2. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Решение. По условию, n=400; k=80; р=0,2; q=0,8. Воспользуемся асимптотической формулой Лапласа:

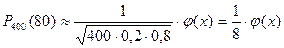
Вычислим определяемое данными задачи значение х:

x = (k-np) / √npq = (80 – 400*0,2) / 8 = 0.

По таблице приложения 1 находим φ(0)=0,3989.

Искомая вероятность

P₄₀₀ (80) = (1/8) * 0,3989 = 0,04986.

Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):

Р₄₀₀ (80)=0,0498.

Пример 3. Вероятность поражения мишени стрелком при одном выстреле р=0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение. По условию, n=10; k=8; р=0,75; q=0,25. Воспользуемся асимптотической формулой Лапласа:

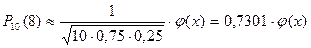
Вычислим определяемое данными задачи значение х:

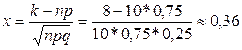
По таблице приложения 1 находим φ (0,36) = 0,3739.

Искомая вероятность равна:

Р ₁₀ (8) = 0,7301 * 0,3739 = 0,273.

Формула Бернулли приводит к иному результату, а именно Р₁₀(8)=0,282. Столь значительное расхождение ответов объясняется тем, что в настоящем примере n имеет малое значение (формула Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях n).