Рассмотрим условия интегрируемости функций на отрезке  , т. е. условия существования определенного интеграла. При определении его как предела интегральной суммы мы предполагали, что функция
, т. е. условия существования определенного интеграла. При определении его как предела интегральной суммы мы предполагали, что функция  ограничена на отрезке
ограничена на отрезке  . Условие ограниченности функций на отрезке
. Условие ограниченности функций на отрезке  является необходимым условием интегрируемости функций, т. е. справедлива следующая
является необходимым условием интегрируемости функций, т. е. справедлива следующая
Теорема. Если 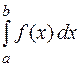 существует, то функция
существует, то функция  ограничена на отрезке
ограничена на отрезке  .
.
Ограниченность является необходимым, но не достаточным условием интегрируемости функции на отрезке  , т. е. что существуют ограниченные функции, не являющиеся интегрируемыми.
, т. е. что существуют ограниченные функции, не являющиеся интегрируемыми.
Сформулируем без доказательства достаточное условие интегрируемости функции.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она интегрируема на этом отрезке, т. е. существует
, то она интегрируема на этом отрезке, т. е. существует 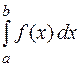 .
.
Отметим, что интеграл Римана существует для значительно более широкого класса функций, нежели рассматриваемый класс непрерывных функций. В частности, справедлива следующая теорема, обобщающая предыдущую теорему
Теорема. Если функция  ограничена на отрезке
ограничена на отрезке  и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке, т. е. существует
и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке, т. е. существует 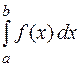 .
.
 2015-06-04
2015-06-04 5158
5158
