Средние и предельные ошибки выборочного наблюдения

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки, которые свойственны только выборочным наблюдениям. Данные показа­тели отражают разность между выборочными и соответствую­щими генеральными показателями.

Средняя ошибкавыборки определяется прежде всего объе­мом выборки и зависит от структуры и степени варьирования изучаемого признака.

Смысл средней ошибки выборки заключается в следующем. Рассчитанные значения выборочной доли (w) и выборочной средней (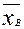)по своей природе случайные величины. Они могут принимать различные значения в зависимости от того, какие кон­кретные единицы генеральной совокупности попадут в выборку. Например, если при определении среднего возраста работников предприятия в одну выборку включить больше молодежи, а в другую — работников старшего возраста, то выборочные средние и ошибки выборки будут разными. Средняя ошибка выборки определяется по формуле:

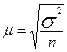(27) или 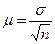- повторная выборка. (28)

Где: μ – средняя ошибка выборки;

σ – среднее квадратическое отклонение признака в генеральной совокупности;

n – объем выборки.

Величина ошибки μ показывает, насколько среднее значение признака, установленное по выборке, отличается от истинного значения признака в генеральной совокупности.

Из формулы следует, что ошибка выборки прямо пропорциональна среднему квадратическому отклонению и обратно пропорциональна корню квадратному из числа единиц, попавших в выборку. Это означает, например, что чем больше разброс значений признака в генеральной совокупности, то есть чем больше дисперсия, тем больше должен быть объем выборки, если мы хотим доверять результатам выборочного обследования. И, наоборот, при малой дисперсии можно ограничиться небольшим числом выборочной совокупности. Ошибка выборки при этом будет находиться в приемлемых пределах.

Поскольку при бесповторном отборе численность генеральной совокупности N в ходе выборки сокращается, то в формулу для расчета средней ошибки выборки включают дополнительный множитель

(1- 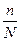). Формула средней ошибки выборки принимает следующий вид:

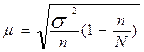. (29)

Средняя ошибка меньше у бесповторной выборки, что и обусловливает ее более широкое применение.

Для практических выводов нужна характеристика генеральной совокупности на основе выборочных результатов. Выборочные средние и доли распространяются на генеральную совокупность с учетом предела их возможной ошибки, причем с гарантирующим ее уровнем вероятности. Задавшись конкретным уровнем вероятности, выбирают величину нормированного отклонения и определяют предельную ошибку выборки.

Надежностью (доверительной вероятностью) оценки Х по Х* называют вероятность γ, с которой осуществляется неравенство

׀Х-Х*׀< δ, (30)

где δ – предельная ошибка выборки, характеризующая ширину интервала, в котором с вероятностью γ находится значение исследуемого параметра генеральной совокупности.

Доверительным называют интервал (Х* - δ; Х* + δ), который покрывает исследуемый параметр Х (то есть значение параметра Х находится внутри этого интервала) с заданной надежностью γ.

Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице: 0,95; 0,99 или 0,999.

Предельная ошибка δ связана со средней ошибкой μ следующим соотношением: 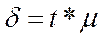, (31)

где: t – коэффициент доверия, зависящий от вероятности P, с которой можно утверждать, что предельная ошибка δ не превысит t-кратную среднюю ошибку μ (его еще называют критическими точками или квантилями распределения Стьюдента).

Как следует из соотношения 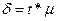, предельная ошибка прямо пропорциональна средней ошибке выборки и коэффициенту доверия, зависящему от заданного уровня надежности оценки.

Из формулы средней ошибки выборки и соотношения предельной и средней ошибок получаем:

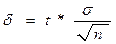. (32)

С учетом доверительной вероятности эта формула примет вид:

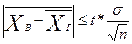. (33)

Коэффициент доверия t определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности. Наиболее часто употребляемые уровни доверительной вероятности и соответствующие им значения t:

P(t)	0,638	0,950	0,954	0,990	0,997
t	1,00	1,96	2,00	2,58	3,00

В случаях малой выборки (объем выборки не более 15-20 единиц) значения коэффициента доверия находят по таблице значений t-распределения Стьюдента. Для этого предварительно задаются значением доверительной вероятности P = γ и определяют число степеней свободы k = n – 1 (n – объем выборки). Затем по таблице находят значение t, соответствующее заданным P и k.

Таблица 10

Обобщенные формулы по теме «Выборочное наблюдение»

	Повторный отбор	Бесповторный отбор
Средняя ошибка выборочной средней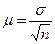
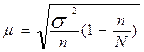
Средняя ошибка выборочной доли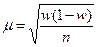
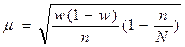
Предельная ошибка выборочной средней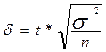
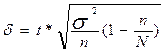
Предельная ошибка выборочной доли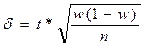

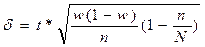
Пример 1: производится выборочная 5%-ная обработка данных об успеваемости студентов 5-го курса дневного отделения ВУЗа одного из факультетов по результатам зимней сессии:

Баллы успеваемости					Всего
Число студентов

Принимая во внимание, что отбор был случайным и бесповторным, определите с вероятностью 0,954 по факультету в целом:

1) пределы, в которых находится средний балл успеваемости в целом по факультету;

2) пределы, в которых находится доля студентов, сдавших экзамены на «хорошо» и «отлично».

Решение:

1) Среднее значение признака в генеральной совокупности находится в интервале: Х* - δ ≤ 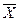≤ Х* + δ.

По формуле средней арифметической взвешенной найдем средний балл успеваемости. 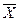= 3,75 балла.

Предельную ошибку выборки определим по формуле для бесповторного отбора:

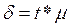или δ = t * 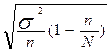= 2 * 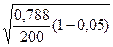= 0,122.

Соответственно, средний балл успеваемости в целом по факультету находится в пределах 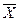±0,122 балла:

3,75 – 0,122 ≤ 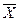≤ 3,75 + 0,122.

С вероятностью 0,954 можно утверждать, что средний балл успеваемости в целом по факультету составляет от 3,628 до 3, 872 балла.

2) доверительные интервалы или пределы доли студентов, сдавших экзамены на «хорошо» и «отлично», представляют собой:

ω - δ ≤ р ≤ ω + δ.

По итогам выборки определяем долю студентов, сдавших экзамены на «хорошо» и «отлично»:

ω = 90 + 40 = 0,65 или 65 %.

Средняя ошибка доли:

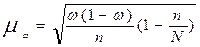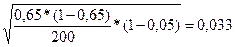= балла.

Предельная ошибка доли:

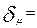t*μ = 2 * 0,033 ≈ 0,066 или 6,6 %.

Таким образом, доля студентов, сдавших экзамены на «хорошо» и «отлично», в генеральной совокупности находится в пределах ω±6,6%:

65 % - 6,6 % ≤ р ≤ 65 % + 6,6 %.

С вероятностью 0,954 можно гарантировать, что доля студентов, сдавших экзамены на «хорошо» и «отлично», составляет от 58,4 до 71,6 % общего числа студентов факультета.