Если случайные величины, образующие систему, зависимы, то для нахождения закона распределения системы недостаточно знать законы распределения отдельных величин, входящих в систему. Требуется еще знать так называемый условный закон распределения одной из них.
Определение. Условным законом распределения одной из величин  , входящих в систему, называется ее закон распределения, вычисленный при условии, что другая случайная величина приняла определенное значение.
, входящих в систему, называется ее закон распределения, вычисленный при условии, что другая случайная величина приняла определенное значение.
Начнем с наиболее простого случая. Пусть случайная величина Y является дискретной.
Определение. Условной функцией распределения 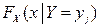 случайной величины X при условии
случайной величины X при условии 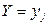 называется условная вероятность события
называется условная вероятность события 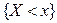 при условии события
при условии события 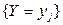 , т.е.
, т.е.
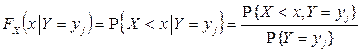 .
.
Аналогично определяется условная функция распределения 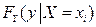 случайной величины Y при условии
случайной величины Y при условии 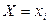 (когда случайная величина X является дискретной):
(когда случайная величина X является дискретной):
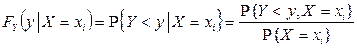 .
.
Замечание 1. Условная функция распределения обладает всеми свойствами, которые присущи обычной (безусловной) функции распределения.
Замечание 2. Если случайная величина X также дискретная, причем 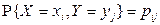 , то удобно рассматривать условную вероятность случайной величине X принять значение
, то удобно рассматривать условную вероятность случайной величине X принять значение 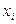 при условии
при условии 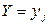 :
:
|
|
|
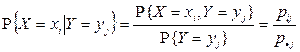 .
.
Обычно условное распределение 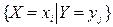 описывают с помощью таблицы. Ясно, что элементы второй строки этой таблицы получаются по формулам
описывают с помощью таблицы. Ясно, что элементы второй строки этой таблицы получаются по формулам 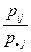 .
.
Аналогично определяется условная вероятность случайной величине Y принять значение 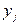 при условии
при условии 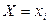 :
:
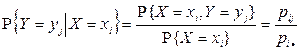
Пример 2.2.20. Закон распределения случайного вектора  задан таблицей:
задан таблицей:
| Y X | ||
| –1 | 0,3 | 0,25 |
| 0,1 | 0,05 | |
| 0,2 | 0,1 |
Описать условные законы распределения: 1) случайной величины X при условии 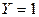 ; 2) случайной величины Y при условии
; 2) случайной величины Y при условии 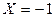 .
.
Решение. Найдем безусловные законы распределения компонент X и Y:
| Y X | 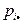
| ||
| –1 | 0,3 | 0,25 | 0,55 |
| 0,1 | 0,05 | 0,15 | |
| 0,2 | 0,1 | 0,3 | |
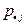
| 0,6 | 0,4 |
1) Условные вероятности случайной величине X принять значения 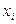 (
(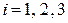 ) при условии
) при условии 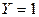 вычисляются по формулам:
вычисляются по формулам:
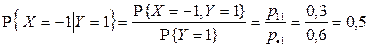 ,
,
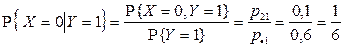 ,
,
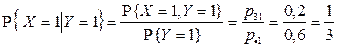 .
.
Тогда условный закон распределения случайной величины X при условии 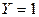 имеет вид:
имеет вид:
| X | –1 | Контроль: | ||
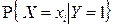
| 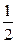
| 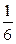
| 
| 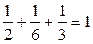
|
2) Условные вероятности случайной величине Y принять значения 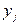 (
(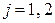 ) при условии
) при условии 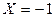 вычисляются по формулам:
вычисляются по формулам:
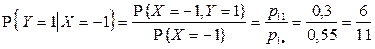 ,
,
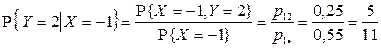 .
.
Тогда условный закон распределения случайной величины Y при условии 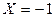 имеет вид:
имеет вид:
| Y | Контроль: | ||
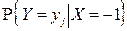
| 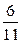
| 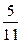
| 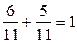
|
В общем случае условную функцию распределения случайной величины X при условии 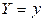 также естественно было бы определить формулой
также естественно было бы определить формулой
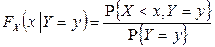 .
.
Однако это не всегда возможно (например, для непрерывной случайной величины Y событие 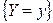 имеет нулевую вероятность). Во избежание этих неприятностей, вместо события
имеет нулевую вероятность). Во избежание этих неприятностей, вместо события 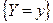 рассматривается событие
рассматривается событие 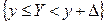 и D устремляется к нулю. Тогда
и D устремляется к нулю. Тогда
|
|
|
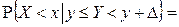
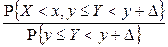
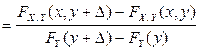 .
.
Тогда условной функцией распределения 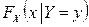 называется предел
называется предел
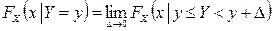 .
.
Оказывается, такой предел всегда существует. Аналогично
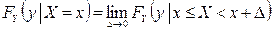
Если случайная величина Y непрерывна, то условную функцию распределения можно определить следующим выражением:
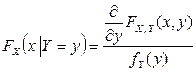 .
.
Аналогично
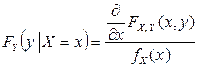 .
.
В наиболее важных для приложений случаях вектор  представляет собой двумерную непрерывную случайную величину с совместной плотностью
представляет собой двумерную непрерывную случайную величину с совместной плотностью 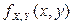 . Тогда
. Тогда
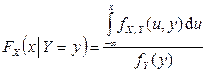 ,
, 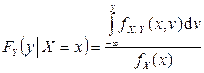 .
.
Нетрудно видеть, что условная функция распределения 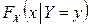 имеет производную по x, т.е. существует условная плотность распределения случайной величины X при условии
имеет производную по x, т.е. существует условная плотность распределения случайной величины X при условии 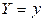 :
:
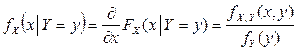 .
.
Аналогично
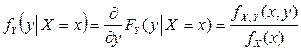 .
.
Пример 2.2.21. В примере 2.2.10 была дана функция плотности 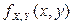 :
:
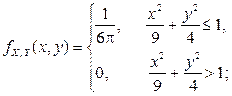
и найдены безусловные плотности распределения компонент X и Y:
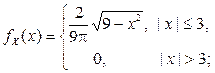
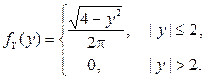
Найти условные плотности распределения компонент X и Y.
Решение. Условные плотности распределения компонент X и Y находятся по формулам 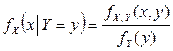 ,
, 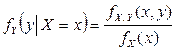 .
.
Поэтому
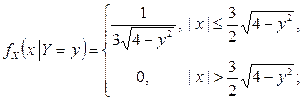
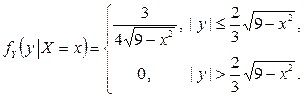
Таким образом, случайная величина X при условии 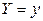 равномерно распределена на отрезке
равномерно распределена на отрезке 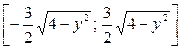 , а случайная величина Y при условии
, а случайная величина Y при условии 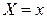 равномерно распределена на отрезке
равномерно распределена на отрезке 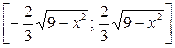 . Условная плотность
. Условная плотность 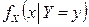 не определена при
не определена при 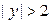 , а условная плотность
, а условная плотность 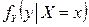 не определена при
не определена при 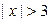 .
.
Пример 2.2.22. Дан двумерный случайный вектор  , где X – время появления в магазине первого покупателя в понедельник, а Y – время появления в магазине первого покупателя во вторник. Установлено, что
, где X – время появления в магазине первого покупателя в понедельник, а Y – время появления в магазине первого покупателя во вторник. Установлено, что 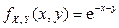 , если
, если 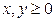 . Найти:
. Найти: 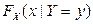 ,
, 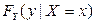 ,
, 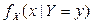 ,
, 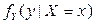 . Установить, зависимы или нет случайные величины X и Y.
. Установить, зависимы или нет случайные величины X и Y.
Решение. Найдем вначале функцию распределения случайного вектора  :
:
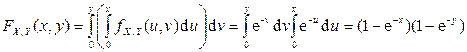 ,
, 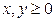 ;
;
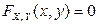 в остальных случаях.
в остальных случаях.
Тогда по свойству 4 совместной функции распределения 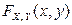 получим:
получим:
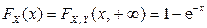 при
при 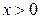 ,
, 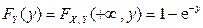 при
при 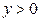 .
.
Отсюда 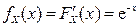 при
при 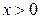 ,
, 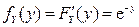 при
при 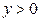 .
.
Найдем теперь условные функции распределения компонент:
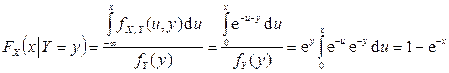 при
при 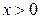 ,
,
аналогично 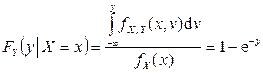 при
при 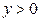 .
.
Получим теперь условные плотности компонент:
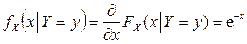 при
при 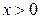 ,
,
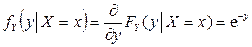 при
при 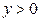 .
.
Поскольку 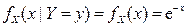 ,
, 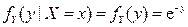 , то
, то 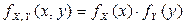 . Поэтому случайные величины X и Y независимы. Это означает, что появление в магазине первого покупателя во вторник не зависит от того, когда в магазин пришел первый покупатель в понедельник.
. Поэтому случайные величины X и Y независимы. Это означает, что появление в магазине первого покупателя во вторник не зависит от того, когда в магазин пришел первый покупатель в понедельник.
Ответ: при положительных x и y 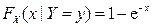 ,
, 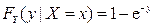 ,
, 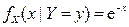 ,
, 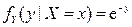 ; случайные величины X и Y независимы.
; случайные величины X и Y независимы.
Пример 2.2.23. Известна плотность совместного распределения непрерывной двумерной случайной величины  :
:
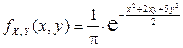 .
.
Найти: 1) плотности распределения компонент X и Y; 2) условные плотности распределения компонент X и Y.
Решение. 1) Найдем вначале плотность распределения компоненты X:
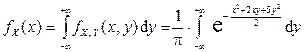 .
.
Вынося за знак интеграла множитель 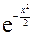 , не зависящий от переменной интегрирования y, и дополнив оставшийся показатель степени до полного квадрата, получим:
, не зависящий от переменной интегрирования y, и дополнив оставшийся показатель степени до полного квадрата, получим:
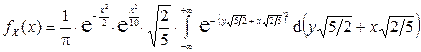 .
.
Учитывая, что интеграл Пуассона 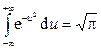 , найдем плотность распределения компоненты X:
, найдем плотность распределения компоненты X:
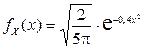 .
.
Аналогично найдем плотность распределения компоненты Y:
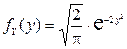 .
.
2) Найдем условные плотности распределения компонент X и Y. Выполнив элементарные выкладки, получим:
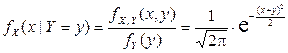 ,
, 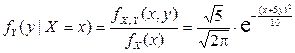 .
.
Ответ: 1) 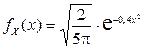 ,
, 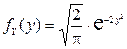 ;
;
2) 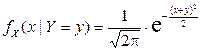 ,
, 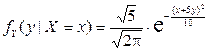 .
.
 2015-06-28
2015-06-28 15067
15067
