Другими словами, индуцированный магнитный момент направлен против поля

В контуре, образуемом движущимся по орбите электроном, в отличие от обычного витка с током, сопротивление равно нулю, поэтому индуцированный магнитным полем ток сохраняется до тех пор, пока существует поле.

Магнитный момент, связанный с этим током, и есть диамагнитный момент.

Для вычисления диамагнитной восприимчивости:

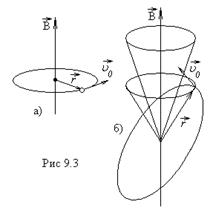рассмотрим круговую электронную орбиту радиуса r (рис.9. 3,а).

Обозначим 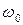угловую скорость движения электрона. Орбитальный магнитный момент (по аналогии с витком с током i) 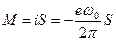. (9.1)

Здесь i — ток в контуре; S — площадь орбиты.

· При наложении магнитного поля:

- угловая скорость изменится на ,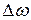

- что и приведет к появлению диамагнитного момента:

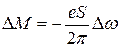. (9.2)

Если мы определим 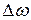, то тем самым найдем индуцированный магнитный момент.

· В отсутствие магнитного поля

- на электрон действует направленная по радиусу сила 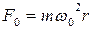, где m — масса электрона. –

· Внесем электронную орбиту в магнитное поле так, чтобы вектор 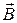был перпендикулярен плоскости орбиты.

При этом на электрон начинает действовать сила Лоренца 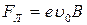, также направленная по радиусу. (Здесь 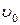— линейная скорость движе­ния электрона; В - индукция поля.)

Результирующая центростремительная сила 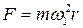представляет собой сумму 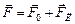, или .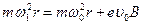

Перепишем это соотношение в виде .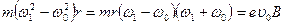

Ясно, что угловая скорость 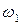не может сильно отличаться от .

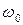Таким образом, .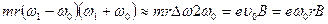

Отсюда

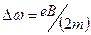. (9.3)

Видно, что магнитное поле приводит к изменению угловой скорости движения электрона по орбите, пропорциональному индукции поля.

Поскольку в выражение (9.3) не входят радиус орбиты и скорость вращения электрона, 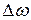для любой орбиты одинаковы.

Если орбита наклонена к полю (рис.9.3,б), т. е. угол между вектором 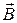и плоскостью орбиты не равен 90°, то под действием поля орбита прецессирует. Нормаль к плоскости орбиты описывает конус относительно направления 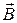с частотой .

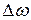Ве­личина 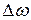получила название частоты Лармора.

Из рис.9. 3,б видно, что в результате прецессии орбиты электрон совершает дополнительное круговое движение вокруг направления поля.

Это и приводит к возникновению магнитного момента, который

· легко вычислить, комбинируя (9.2) и (9.3): .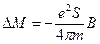

· Магнитный момент 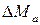многоэлектронного атома складывается из моментов отдельных электронов.

· Если в атоме име­ется z электронов, то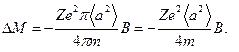

Здесь < а ²> — средний квадрат расстояния электронов от оси, проходящей через ядро параллельно полю.

· Для сферически симметричного атома < а ²>=²/з< r ²>.

Поэтому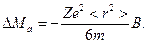

· Если в единичном объеме вещества содержится N атомов, то

Намагниченность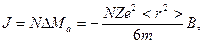

и диамагнитная восприимчивость (для единичного объема)

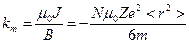(9.4)

Из (9.4) следует, что диамагнитная восприимчивость

· не зависит от температуры

· возрастает пропорционально порядковому номеру элемента.

Это хорошо согласуется с экспериментом.

Полагая 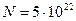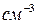, 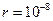см, получим .

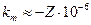Поскольку диамагнетизм связан с орбитальным движением электронов в атомах, он присущ всем телам без исключения, т. е. является универсальным магнитным свойством.

В любых веществах независимо от их агрегатного состояния или структуры диамагнетизм присутствует. Однако часто он перекрывается более сильными магнитными эффектами — парамагнетизмом или ферромагнетизмом.