Классические методы определения экстремумов

Нелинейное программирование.

Как знаем, математическая модель оптимизационной задачи по планированию и управлению сложными системами, в том числе экономическими системами, в общей постановке можно сформулировать в следующем виде:

найти значения переменных х₁, х₂, …, х_n, удовлетворяющие системе ограничений (неравенств или уравнений)

φ_i (х₁, х₂, …, х_n) ≤ b_i, i=1, 2, …, m (7.1)

и обеспечивающие максимум (минимум) целевой функции

Z = f(х₁, х₂, …, х_n)→max (min). (7.2)

Во многих практических задачах исследования операций, в том числе в экономических моделях, зависимости между постоянными и переменными факторами в функциях (7.1) и (7.2) лишь в первом приближении можно считать линейными. Более детальное рассмотрение позволяет обнаружить их нелинейность. Как правило, такие показатели, как прибыль, себестоимость, капитальные затраты на производство и т.д., в действительности зависят от объема производства, расхода ресурсов и т.п. нелинейно. В этом случае возникает задача нелинейного программирования.

Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Допустим, что среди ограничений (7.1) нет неравенств, не обязательны условия неотрицательности, переменные являются дискретными, m<n, а функции φ_i(Х) и f (Х) непрерывны и имеют частные производные по крайней мере второго порядка.

Такие задачи в принципе можно решить классическими методами дифференциального исчисления. Однако на этом пути встречаются такие вычислительные трудности, которые делают необходимым поиск других методов решения.

Так, казалось бы, найдя частные производные функции f по всем аргументам, приравняв их нулю и решив систему уравнений 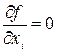, получим значения x _j, при которых функция f может достичь своего экстремума.

Однако, эти методы имеют существенные недостатки: во-первых, при большом количестве переменных решение получаемой системы дифференциальных уравнений является довольно громоздкой задачей; во-вторых, классические методы позволяют найти критические точки только внутри области определения функции и не позволяют исследовать граничные точки; в-третьих, эти методы позволяют определить только локальные экстремумы функции, и не пригодны для отыскания глобального экстремума, так как не учитывают взаимовлияния параметров, в-четвертых, классические методы вовсе неприменимы, если x_j или функция f(Х) - дискретные величины.

Поэтому классические методы часто используются не в качестве вычислительного средства, а как основа для теоретического анализа.

Как правило, функции φ_i и f могут иметь произвольный нелинейный вид.

Используя классические методы оптимизации, следует четко представлять себе различие между локальным, глобальным и условным экстремумами функции.

Будем полагать, что функция Z = f(х₁, х₂, …, х_n)=f(X) дважды дифференцируема в точке Х* = (х*₁, х*₂, …, х*_n), (Х*ЄD(f)) и в некоторой ее окрестности. Говорят, что функция f(X) имеет экстремум в точке Х* (максимум или минимум), если для всех точек Х этой окрестности выполняются условия f(X*)≥f(X) (в задачах на max f) или f(X*) ≤ f(X) (в задачах на min f),

На рис. 7.1 приведен график функции одной переменной, которая на промежутке D(a; b) имеет точки экстремумов х_о, х₁, х₂ и х₃

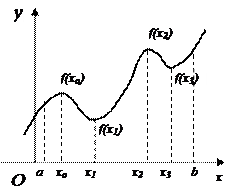Экстремум функции в достаточно малой окрестности точки х_о называют локальным экстремумом. На одном промежутке функция может иметь несколько локальных экстремумов.

Рис. 7.1.

Причем может случиться, что локальный минимум в одной окрестности больше локального максимума в другой окрестности, например, на рис. 7.1 минимум в окрестности точки х₃ больше максимума в окрестности точки х_о, то есть, f_min(x₃)>f_max(x₁).

Наибольшее или наименьшее значения локальных экстремумов на некотором промежутке D называется глобальным максимумом (минимумом) функции на данном промежутке.