Понятие множества. Подмножества. Операции над множествами. Алгебра множеств.
Т.е., можно сказать, что множество – это определенная совокупность различных объектов (предметов или понятий), объединенных в одно целое. Объекты. Обычно множества обозначают прописными латинскими буквами, а их элементы – Конечное множество можно задать перечислением его элементов. При задании множества в форме списка непосредственно.
Подмножества.
Каждое непустое множество имеет по крайней мере два подмножества: 1) пустое множество является подмножеством любого множества Æ; 2) каждое множество является подмножеством самого себя.
Операции над множествами
3.1 Объединением (суммой) двух множеств  и
и  называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Объединение записывается как
называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Объединение записывается как
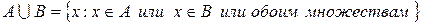 .
.
Пример.
Пусть 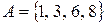 и
и 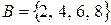 . Тогда объединение
. Тогда объединение  и
и  есть
есть 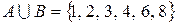 . При этом элементы 6 и 8 принадлежат обоим множествам.
. При этом элементы 6 и 8 принадлежат обоим множествам.
Аналогично определяется объединение более чем двух множеств. Объединение трех множеств  ,
,  и
и 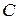 есть множество
есть множество 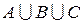 , каждый, из элементов которого принадлежит хотя бы одному из множеств
, каждый, из элементов которого принадлежит хотя бы одному из множеств  ,
,  и
и 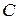 :
:
|
|
|
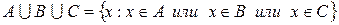 .
.
3.2 Пересечением (произведением) двух множеств  и
и  называется новое множество,состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств
называется новое множество,состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств  и
и  .
.
Пересечение записывается как 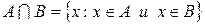 .
.
Пример. Пусть 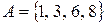 и
и 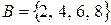 . Тогда
. Тогда 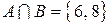 .
.
Пересечение более чем двух множеств определяется аналогичным образом. Пересечение трех множеств  ,
,  и
и 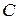 есть множество элементов, которые принадлежат
есть множество элементов, которые принадлежат  ,
,  и
и 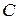 :
: 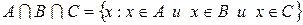 .
.
Если множества  и
и  не имеют общих элементов, то их пересечение пусто:
не имеют общих элементов, то их пересечение пусто: 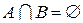 . Такие множества
. Такие множества  и
и  называются непересекающимися.
называются непересекающимися.
Пример. Пусть  – множество целых положительных чисел, а
– множество целых положительных чисел, а  – множество целых отрицательных чисел. Тогда
– множество целых отрицательных чисел. Тогда  и
и  – непересекающиеся множества, так как не существует целых чисел, которые были бы одновременно и положительными, и отрицательными.
– непересекающиеся множества, так как не существует целых чисел, которые были бы одновременно и положительными, и отрицательными.
Определение непересекающихся множеств может быть распространено на случай более чем двух множеств.
Говорят, что 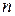 множеств
множеств 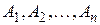 являются взаимно непересекающимися (или попарно непересекающимися), если никакие два из этих множеств не имеют общих элементов. Иными словами, множества
являются взаимно непересекающимися (или попарно непересекающимися), если никакие два из этих множеств не имеют общих элементов. Иными словами, множества 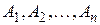 взаимно непересекающиеся, если
взаимно непересекающиеся, если 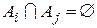 при
при 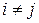 для
для 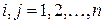 .
.
3.3 Разбиение множества на подмножества. В основе всевозможных классификаций, применяемых в биологии, лингвистике и других науках, лежит операция разбиения множества на попарно непересекающиеся подмножества. Одно и то же множество можно разбивать на подмножества разными способами: совокупность людей можно разделить на детей и взрослых, на мужчин и женщин.
Разбиение множества  есть набор его подмножеств
есть набор его подмножеств 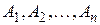 , которые взаимно не пересекаются и в объединении дают
, которые взаимно не пересекаются и в объединении дают  . Это записывается так:
. Это записывается так: 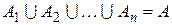 и
и 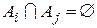 при
при 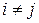 для
для 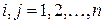 .
.
|
|
|
Пример. 1) Множество натуральных чисел разбивается на подмножества четных и нечетных чисел. 2) Множество всех многоугольников разбивается на множества треугольников, четырехугольников, пятиугольников и т.д.
3.4 Разностью двух множеств  и
и  называется множество, элементами которого являются те и только те элементы множества
называется множество, элементами которого являются те и только те элементы множества  , которые не принадлежат
, которые не принадлежат  . При этом предполагается, что множество
. При этом предполагается, что множество  не является частью множества
не является частью множества  . Разность множеств
. Разность множеств  и
и  обозначается
обозначается 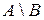 и по определению
и по определению 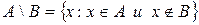 . Таким образом, при вычитании множества
. Таким образом, при вычитании множества  из множества
из множества  из
из  удаляют пересечение
удаляют пересечение  и
и  :
: 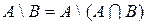 .
.
Пример.
1) Пусть  – множество студентов данной группы института,
– множество студентов данной группы института,  – множество девушек, обучающихся в этом институте. Тогда
– множество девушек, обучающихся в этом институте. Тогда 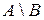 – множество всех юношей, обучающихся в данной группе этого института.
– множество всех юношей, обучающихся в данной группе этого института.
2) Пусть 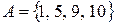 ,
, 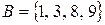 . Тогда
. Тогда 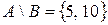 и
и 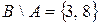 .
.
3.5 В случае, когда  – часть множества
– часть множества  ,
, 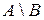 называют дополнением к
называют дополнением к  в множестве
в множестве  и обозначают
и обозначают 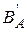 .
.
Пример. Пусть  – множество четных чисел,
– множество четных чисел,  – множество целых чисел. Тогда
– множество целых чисел. Тогда 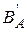 – множество нечетных чисел.
– множество нечетных чисел.
3.6 Часто все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого определенного фиксированного множества. Это множество называют универсальным и обозначают 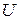 .
.
Дополнением множества  по отношению к универсальному множеству
по отношению к универсальному множеству 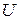 есть множество
есть множество 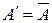 , составленное из всех тех элементов
, составленное из всех тех элементов 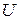 , которые не находятся в
, которые не находятся в  :
:
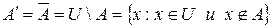 .
.
Пример. Для учебной группы института определим  как множество всех юношей этой группы, а
как множество всех юношей этой группы, а  – как множество студентов группы, сдавших экзамены. Универсальным множеством
– как множество студентов группы, сдавших экзамены. Универсальным множеством 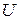 является множество всех студентов этой группы. Тогда
является множество всех студентов этой группы. Тогда 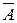 – множество девушек этой группы;
– множество девушек этой группы; 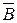 – студенты, не сдавшие экзамены;
– студенты, не сдавшие экзамены; 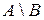 – юноши, не сдавшие экзамены;
– юноши, не сдавшие экзамены; 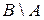 – девушки, сдавшие экзамены.
– девушки, сдавшие экзамены.
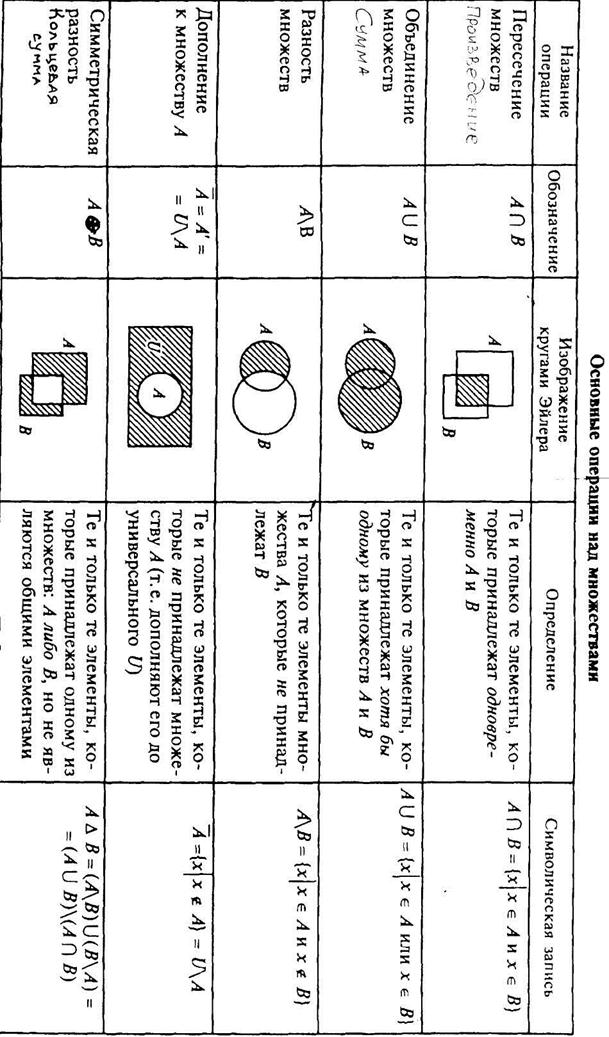
Для наглядного изображения множеств и их свойств используются диаграммы Эйлера–Венна. В этом случае множество будем изображать кругом на плоскости, и представлять элементы множества как множество точек круга. Универсальное множество 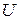 будем изображать множеством точек некоторого прямоугольника. Если изобразить кругами множества
будем изображать множеством точек некоторого прямоугольника. Если изобразить кругами множества  и
и  , то множества
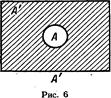
, то множества 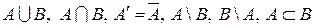 изобразятся следующими заштрихованными областями:
изобразятся следующими заштрихованными областями:
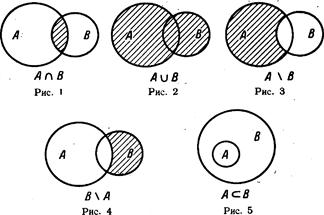
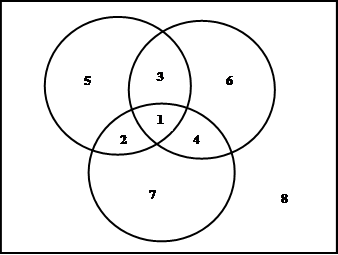
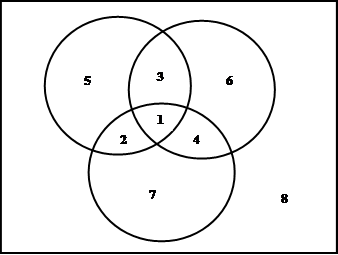
Для случая трех множеств на рисунке представлены все восемь возможностей принадлежности некоторого элемента трем данным множествам. Область, отмеченная цифрой 1, изображает множество элементов, принадлежащих всем трем множествам. Элементы, принадлежащие только двум из трех данных множеств, попадают в области 2, 3, 4, а элементы, принадлежащие только одному из трех данных множеств, попадают в области 5, 6 и 7. Множество элементов, не принадлежащих ни одному из трех данных множеств, соответствует внешней области, отмеченной цифрой 8. Все возможности принадлежности элемента трем данным множествам исчерпаны.
 |
Теория нечетких множеств (fuzzy sets theory) ведет свое начало с 1965г., когда профессор Лотфи Заде (Lotfi Zadeh) из университета Беркли опубликовал основополагающую работу “ Fuzzy Sets ” в журнале “ Information and Control ”. Прилагательное " fuzzy ", которое можно перевести на русский как нечеткий, размытый, ворсистый, пушистый, введено в название новой теории с целью дистанцирования от традиционной четкой математики и Аристотелевой логики, оперирующих с четкими понятиями: “принадлежит - не принадлежит”, “истина - ложь”. Концепция нечеткого множества зародилась у Заде “как неудовлетворенность математическими методами классической теории систем, которая вынуждала добиваться искусственной точности, неуместной во многих системах реального мира, особенно в так называемых гуманистических системах, включающих людей”.
|
|
|
Началом практического применения теории нечетких множеств можно считать 1975 г., когда Мамдани и Ассилиан (Mamdani and Assilian) построили первый нечеткий контролер для управления простым паровым двигателем. В 1982 Холмблад и Остергад (Holmblad and Osregaad) разработали первый промышленный нечеткий контроллер, который был внедрен в управление процессом обжига цемента на заводе в Дании. Успех первого промышленного контролера, основанного на нечетких лингвистических правилах “Если - то” привел к всплеску интереса к теории нечетких множеств среди математиков и инженеров. Несколько позже Бартоломеем Коско (Bart Kosko) была доказана теорема о нечеткой аппроксимации (Fuzzy Approximation Theorem), согласно которой любая математическая система может быть аппроксимирована системой, основанной на нечеткой логике. Другими словами, с помощью естественно-языковых высказываний-правил “Если - то”, с последующей их формализацией средствами теории нечетких множеств, можно сколько угодно точно отразить произвольную взаимосвязь “входы-выход” без использования сложного аппарата дифференциального и интегрального исчислений, традиционно применяемого в управлении и идентификации.
Системы, основанные на нечетких множествах разработаны и успешно внедрены в таких областях, как: управление технологическими процессами, управление транспортом, медицинская диагностика, техническая диагностика, финансовый менеджмент, биржевое прогнозирование, распознавание образов. Спектр приложений очень широкий - от видеокамер и бытовых стиральных машин до средств наведения ракет ПВО и управления боевыми вертолетами. Практический опыт разработки систем нечеткого логического вывода свидетельствует, что сроки и стоимость их проектирования значительно меньше, чем при использовании традиционного математического аппарата, при этом обеспечивается требуемый уровень робастности и прозрачности моделей.
Далее рассматриваются основные термины и понятия теории нечетких множеств. При этом основное внимание уделяется прикладным вопросам их использования в пакете прикладных программ Fuzzy Logic Toolbox. Терминология приводится на английском языке с целью облегчения работы пользователям с англоязычным пакетом Fuzzy Logic Toolbox.
|
|
|
ОСНОВНЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
Понятие нечеткого множества - эта попытка математической формализации нечеткой информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать к данному множеству с различной степенью. При таком подходе высказывания типа “такой-то элемент принадлежит данному множеству” теряют смысл, поскольку необходимо указать “насколько сильно” или с какой степенью конкретный элемент удовлетворяет свойствам данного множества.
Определение 1. Нечетким множеством (fuzzy set) 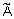 на универсальном множестве U называется совокупность пар (
на универсальном множестве U называется совокупность пар (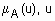 ), где
), где 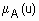 - степень принадлежности элемента
- степень принадлежности элемента  к нечеткому множеству
к нечеткому множеству 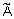 . Степень принадлежности - это число из диапазона [0, 1]. Чем выше степень принадлежности, тем в большей мерой элемент универсального множества соответствует свойствам нечеткого множества.
. Степень принадлежности - это число из диапазона [0, 1]. Чем выше степень принадлежности, тем в большей мерой элемент универсального множества соответствует свойствам нечеткого множества.
Определение 2. Функцией принадлежности (membership function) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.
Если универсальное множество состоит из конечного количества элементов 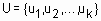 , тогда нечеткое множество
, тогда нечеткое множество 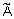 записывается в виде
записывается в виде 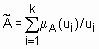 . В случае непрерывного множества U используют такое обозначение
. В случае непрерывного множества U используют такое обозначение 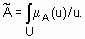
Примечание: знаки 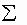 и
и 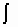 в этих формулах означают совокупность пар
в этих формулах означают совокупность пар 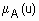 и u.
и u.
Пример 1. Представить в виде нечеткого множества понятие “мужчина среднего роста”.
Решение: 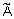 = 0/155+0.1/160 + 0.3/165 + 0.8/170 +1/175 +1/180 + 0.5/185 +0/180.
= 0/155+0.1/160 + 0.3/165 + 0.8/170 +1/175 +1/180 + 0.5/185 +0/180.
Определение 3. Лингвистической переменной (linguistic variable) называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка.
Определение 4. Терм–множеством (term set) называется множество всех возможных значений лингвистической переменной.
Определение 5. Термом (term) называется любой элемент терм–множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности.
Пример 2. Рассмотрим переменную “ скорость автомобиля ”, которая оценивается по шкале “ низкая ", " средняя ", " высокая ” и “ очень высокая ".
В этом примере лингвистической переменной является “ скорость автомобиля ”, термами - лингвистические оценки “ низкая ", " средняя ", " высокая ” и “ очень высокая ”, которые и составляют терм–множество.
Определение 6. Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число.
В теории нечетких множеств процедура дефаззификации аналогична нахождения характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа ограничивается лишь одноэкстремальными функциями принадлежности. Для многоэкстремальных функций принадлежности в Fuzzy Logic Toolbox запрограммированы такие методы дефаззификации:
Centroid - центр тяжести;
Bisector - медиана;
LOM (Largest Of Maximums) - наибольший из максимумов;
SOM (Smallest Of Maximums) - наименьший из максимумов;
Mom (Mean Of Maximums) - центр максимумов.
Определение 7. Дефаззификация нечеткого множества 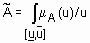 по методу центра тяжести осуществляется по формуле
по методу центра тяжести осуществляется по формуле 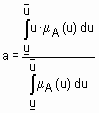 .
.
Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества. В случае дискретного универсального множества дефаззификация нечеткого множества 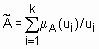 по методу центра тяжести осуществляется по формуле
по методу центра тяжести осуществляется по формуле 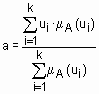 .
.
Определение 8. Дефаззификация нечеткого множества 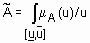 по методу медианы состоит в нахождении такого числа a, что
по методу медианы состоит в нахождении такого числа a, что 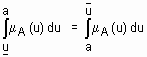 .
.
Геометрической интерпретацией метода медианы является нахождения такой точки на оси абцисс, что перпендикуляр, восстановленный в этой точке, делит площадь под кривой функции принадлежности на две равные части. В случае дискретного универсального множества дефаззификация нечеткого множества 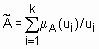 по методу медианы осуществляется по формуле
по методу медианы осуществляется по формуле 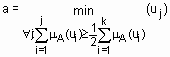 .
.
Определение 9. Дефаззификация нечеткого множества 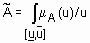 по методу центра максимумов осуществляется по формуле:
по методу центра максимумов осуществляется по формуле:
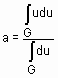 ,
,
где G – множество всех элементов из интервала 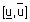 , имеющих максимальную степень принадлежности нечеткому множеству
, имеющих максимальную степень принадлежности нечеткому множеству 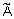 .
.
В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей. Если множество таких элементов конечно, то формула из определения 9 упрощается к следующему виду:
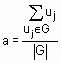 ,
,
где 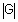 - мощность множества G.
- мощность множества G.
В дискретном случае дефаззификация по методам наибольшего из максимумов и наименьшего из максимумов осуществляется по формулам 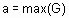 и
и  , соответственно. Из последних трех формулы видно, что если функция принадлежности имеет только один максимум, то его координата и является четким аналогом нечеткого множества.
, соответственно. Из последних трех формулы видно, что если функция принадлежности имеет только один максимум, то его координата и является четким аналогом нечеткого множества.
Пример 3. Провести дефаззификацию нечеткого множества “мужчина среднего роста ” из примера 1 по методу центра тяжести.
Решение: Применяя формулу из определения 7, получаем:
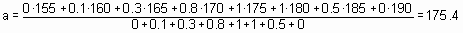
Определение 10. Нечеткой базой знаний (fuzzy knowledge base) о влиянии факторов 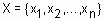 на значение параметра y называется совокупность логических высказываний типа:
на значение параметра y называется совокупность логических высказываний типа:
ЕСЛИ 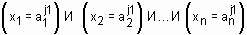
ИЛИ 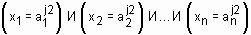 …
…
ИЛИ 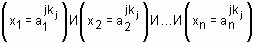 ,
,
ТО 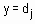 , для всех
, для всех 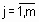 ,
,
где 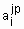 - нечеткий терм, которым оценивается переменная
- нечеткий терм, которым оценивается переменная 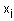 в строчке с номером jp (
в строчке с номером jp (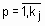 );
);
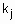 - количество строчек-конъюнкций, в которых выход y оценивается нечетким термом
- количество строчек-конъюнкций, в которых выход y оценивается нечетким термом 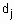 ,
, 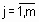 ;
;
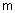 - количество термов, используемых для лингвистической оценки выходного параметра y.
- количество термов, используемых для лингвистической оценки выходного параметра y.
С помощью операций 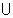 (ИЛИ) и
(ИЛИ) и 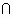 (И) нечеткую базу знаний из определения 10 перепишем в более компактном виде:
(И) нечеткую базу знаний из определения 10 перепишем в более компактном виде:
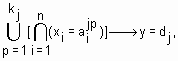
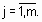 (1)
(1)
Определение 11. Нечетким логическим выводом (fuzzy logic inference) называется апроксимация зависимости 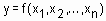 с помощью нечеткой базы знаний и операций над нечеткими множествами.
с помощью нечеткой базы знаний и операций над нечеткими множествами.
Пусть 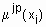 - функция принадлежности входа
- функция принадлежности входа 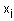 нечеткому терму
нечеткому терму 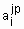 ,
, 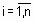 ,
, 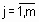 ,
, 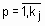 , т. е.
, т. е. 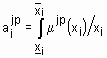 ;
; 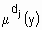 - функция принадлежности выхода y нечеткому терму
- функция принадлежности выхода y нечеткому терму 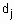 ,
, 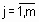 , т. е.
, т. е. 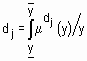 . Тогда степень принадлежности конкретного входного вектора
. Тогда степень принадлежности конкретного входного вектора 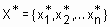 нечетким термам
нечетким термам 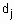 из базы знаний (1) определяется следующей системой нечетких логических уравнений:
из базы знаний (1) определяется следующей системой нечетких логических уравнений:
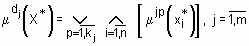 , (2)
, (2)
где 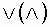 - операция максимума (минимума).
- операция максимума (минимума).
Нечеткое множество 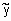 , соответствующее входному вектору
, соответствующее входному вектору 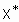 , определяется следующим образом:
, определяется следующим образом:
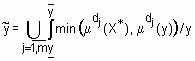 , (3)
, (3)
где 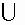 - операция объединения нечетких множеств.
- операция объединения нечетких множеств.
Четкое значение выхода y, соответствующее входному вектору 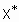 определяется в результате деффаззификации нечеткого
определяется в результате деффаззификации нечеткого 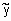 .
.
СВОЙСТВА НЕЧЕТКИХ МНОЖЕСТВ
Определение 12. Высотой нечеткого множества 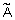 называется верхняя граница его функции принадлежности:
называется верхняя граница его функции принадлежности: 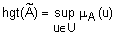 . Для дискретного универсального множества
. Для дискретного универсального множества 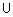 супремум становится максимумом, а значит высотой нечеткого множества будет максимум степеней принадлежности его элементов
супремум становится максимумом, а значит высотой нечеткого множества будет максимум степеней принадлежности его элементов
Определение 13. Нечеткое множество 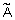 называется нормальным, если его высота равна единице. Нечеткие множества не являющиеся нормальными называются субнормальными. Нормализация преобразование субнормального нечеткого множества
называется нормальным, если его высота равна единице. Нечеткие множества не являющиеся нормальными называются субнормальными. Нормализация преобразование субнормального нечеткого множества 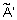 в нормальное
в нормальное 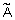 определяется так:
определяется так:
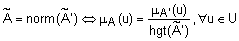 . В качестве примера на рис. 1 показана нормализация нечеткого множества
. В качестве примера на рис. 1 показана нормализация нечеткого множества 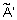 с функцией принадлежности
с функцией принадлежности 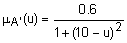 .
.
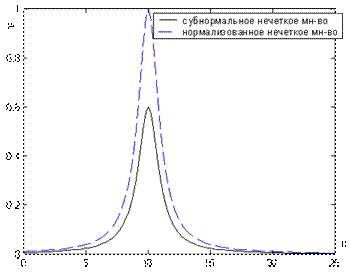
Рисунок 1 - Нормализация нечеткого множества
Определение 14. Носителем нечеткого множества 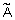 называется четкое подмножество универсального множества
называется четкое подмножество универсального множества 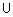 , элементы которого имеют ненулевые степени принадлежности:
, элементы которого имеют ненулевые степени принадлежности: 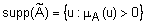 .
.
Определение 15. Нечеткое множество называется пустым, если его носитель является пустым множеством.
Определение 16. Ядром нечеткого множества 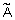 называется четкое подмножество универсального множества
называется четкое подмножество универсального множества 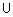 , элементы которого имеют степени принадлежности равные единице:
, элементы которого имеют степени принадлежности равные единице: 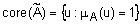 . Ядро субнормального нечеткого множества пустое.
. Ядро субнормального нечеткого множества пустое.
Определение 17. 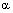 - сечением (или множеством
- сечением (или множеством 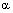 -уровня) нечеткого множества
-уровня) нечеткого множества 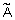 называется четкое подмножество универсального множества
называется четкое подмножество универсального множества 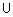 , элементы которого имеют степени принадлежности большие или равные
, элементы которого имеют степени принадлежности большие или равные 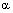 :
: 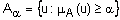 ,
, 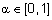 . Значение
. Значение 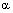 называют
называют 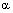 -уровнем. Носитель (ядро) можно рассматривать как сечение нечеткого множества на нулевом (единичном)
-уровнем. Носитель (ядро) можно рассматривать как сечение нечеткого множества на нулевом (единичном) 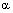 -уровне.
-уровне.
Рис. 2 иллюстрирует определения носителя, ядра, 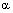 -сечения и
-сечения и 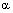 -уровня нечеткого множества.
-уровня нечеткого множества.
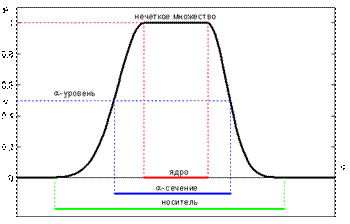
Рисунок 2 - Ядро, носитель и 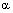 -сечение нечеткого множества
-сечение нечеткого множества
Определение 18. Нечеткое множество 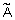 называется выпуклым если:
называется выпуклым если: 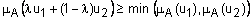 ,
, 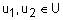 ,
, 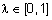 . Альтернативное определение: нечеткое множество будет выпуклым, если все его
. Альтернативное определение: нечеткое множество будет выпуклым, если все его 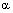 -сечения - выпуклые множества. На рис. 3 приведены примеры выпуклого и невыпуклого нечетких множеств.
-сечения - выпуклые множества. На рис. 3 приведены примеры выпуклого и невыпуклого нечетких множеств.
Определение 19. Нечеткие множества 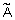 и
и 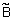 равны (
равны (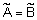 ) если
) если 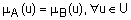 .
.
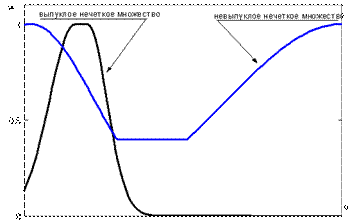
Рисунок 3 - К определению выпуклого нечеткого множества
ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
Определения нечетких теоретико-множественных операций объединения, пересечения и дополнения могут быть обобщены из обычной теории множеств. В отличие от обычных множеств, в теории нечетких множеств степень принадлежности не ограничена лишь бинарной значениями 0 и 1 она может принимать значения из интервала [0, 1]. Поэтому, нечеткие теоретико-множественные операции могут быть определены по-разному. Ясно, что выполнение нечетких операций объединения, пересечения и дополнения над не нечеткими множествами должно дать такие же результаты, как и при использование обычных канторовских теоретико-множественных операций. Ниже приведены определения нечетких теоретико-множественных операций, предложенных Л. Заде.
Определение 20. Дополнением нечеткого множества 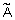 заданного на
заданного на 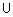 называется нечеткое множество
называется нечеткое множество 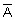 с функцией принадлежности
с функцией принадлежности 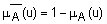 для всех
для всех 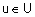 . На рис. 4 приведен пример выполнения операции нечеткого дополнения.
. На рис. 4 приведен пример выполнения операции нечеткого дополнения.
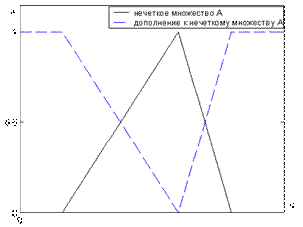
Рисунок 4 - Дополнение нечеткого множества
Определение 21. Пересечением нечетких множеств 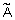 и
и 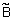 заданных на
заданных на 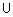 называется нечеткое множество
называется нечеткое множество 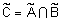 с функцией принадлежности
с функцией принадлежности 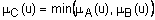 для всех
для всех 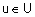 . Операция нахождения минимума также обозначается знаком
. Операция нахождения минимума также обозначается знаком 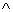 , т.е.
, т.е. 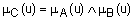 .
.
Определение 22. Объединением нечетких множеств 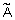 и
и 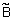 заданных на
заданных на 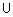 называется нечеткое множество
называется нечеткое множество 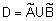 с функцией принадлежности
с функцией принадлежности 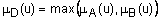 для всех
для всех 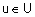 . Операция нахождения максимума также обозначается знаком
. Операция нахождения максимума также обозначается знаком 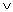 , т.е.
, т.е. 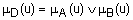 .
.
Обобщенные определения операций нечеткого пересечения и объединения - треугольной нормы (t-нормы) и треугольной конормы (t-конормы или s-нормы) приведены ниже.
Определение 23. Треугольной нормой (t-нормой) называется бинарная операция 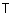 на единичном интервале
на единичном интервале 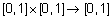 , удовлетворяющая следующим аксиомам для любых
, удовлетворяющая следующим аксиомам для любых 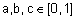 :
:
1.
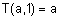 (граничное условие);
(граничное условие);
2.
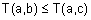 если
если 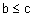 (монотонность);
(монотонность);
3.
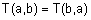 (коммутативность);
(коммутативность);
4.
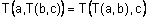 (ассоциативность).
(ассоциативность).
Наиболее часто используются такие t-нормы: пересечение по Заде 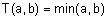 ; вероятностное пересечение
; вероятностное пересечение 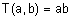 ; пересечение по Лукасевичу
; пересечение по Лукасевичу 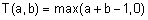 . Примеры выполнения пересечения нечетких множеств с использованием этих t-норм показаны на рис. 5.
. Примеры выполнения пересечения нечетких множеств с использованием этих t-норм показаны на рис. 5.
Определение 24. Треугольной конормой (s-нормой) называется бинарная операция 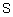 на единичном интервале
на единичном интервале 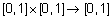 , удовлетворяющая следующим аксиомам для любых
, удовлетворяющая следующим аксиомам для любых 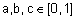 :
:
1.
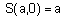 (граничное условие);
(граничное условие);
2.
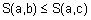 если
если 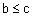 (монотонность);
(монотонность);
3.
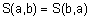 (коммутативность);
(коммутативность);
4.
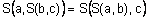 (ассоциативность).
(ассоциативность).
Наиболее часто используются такие s-нормы: объединение по Заде 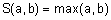 ; вероятностное объединение
; вероятностное объединение 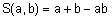 ; объединение по Лукасевичу
; объединение по Лукасевичу 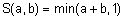 . Примеры выполнения объединения нечетких множеств с использованием этих s-норм показаны на рис. 6.
. Примеры выполнения объединения нечетких множеств с использованием этих s-норм показаны на рис. 6.
Наиболее известные треугольные нормы приведены в табл. 1.
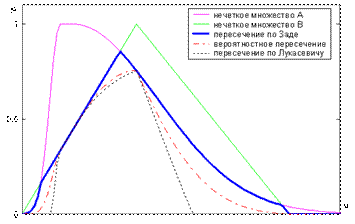
Рисунок 5 - Пересечение нечетких множеств с использованием различных t-норм
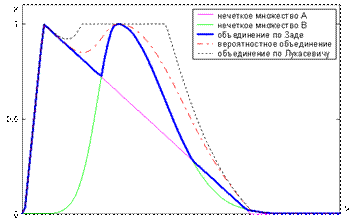
Рисунок 6 - Объединение нечетких множеств с использованием различных s-норм
Таблица 1 - Примеры треугольных норм
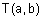 |
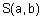 |
Параметр |
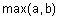 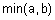 |
||
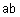 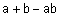 |
||
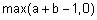 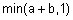 |
||
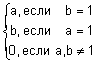 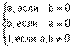 |
||
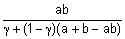 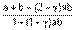 |
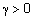 |
|
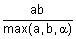 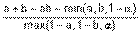 |
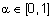 |
|
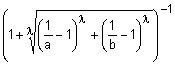 |
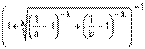 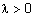 |
|
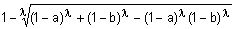 |
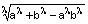 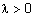 |
|
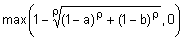 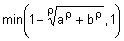 |
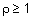 |
|
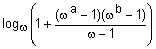 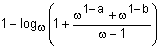 |
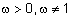 |
|
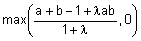 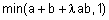 |
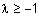 |
В процессе обучения сеть в определенном порядке просматривает обучающую выборку. Порядок просмотра может быть последовательным, случайным и т. д. Некоторые сети,обучающиеся без учителя (например, сети Хопфилда), просматривают выборку только один раз. Другие (например, сети Кохонена), а также сети, обучающиеся с учителем, просматривают выборку множество раз, при этом один полный проход по выборке называется эпохой обучения. При обучении с учителем набор исходных данных делят на две части — собственно обучающую выборку и тестовые данные; принцип разделения может быть произвольным. Обучающие данные подаются сети для обучения, а проверочные используются для расчета ошибки сети (проверочные данные никогда для обучения сети не применяются).
Таким образом, если на проверочных данных ошибка уменьшается, то сеть действительно выполняет обобщение. Если ошибка на обучающих данных продолжает уменьшаться, а ошибка на тестовых данных увеличивается, значит, сеть перестала выполнять обобщение и просто «запоминает» обучающие данные. Это явление называется переобучением сети или оверфиттингом. В таких случаях обучение обычно прекращают. В процессе обучения могут проявиться другие проблемы, такие какпаралич или попадание сети в локальный минимум поверхности ошибок. Невозможно заранее предсказать проявление той или иной проблемы, равно как и дать однозначные рекомендации к их разрешению.
Все выше сказанное относится только к итерационным алгоритмам поиска нейросетевых решений. Для них действительно нельзя ничего гарантировать и нельзя полностью автоматизировать обучение нейронных сетей. Однако, наряду с итерационными алгоритмами обучения, существуют не итерационные алгоритмы, обладающие очень высокой устойчивостью и позволяющие полностью автоматизировать процесс обучения.
 2015-07-14
2015-07-14 77516
77516