Основные операции над множествами

Объединение (теоретико-множественная сумма) множеств А и В - множество С, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А, В:

С = А 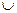В = { x | xÎ A Ú xÎ B },

где 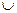- знак теоретико-множественного сложения, а Ú - логический знак “или”. Сумму множеств А и В довольно часто обозначают А+В (если это не вызывает неоднозначности).

Обобщение операции объединения (сложения) для произвольного числа (системы) множеств S = { A,B,C,…,G }

U = A+B+C+…+G = { x | xÎ A Ú xÎ B Ú xÎ C Ú…Ú xÎ G }.

Из определения операции объединения и последнего равенства следует – любой элемент системы S является некоторым подмножеством множества U, т.е. данное множество, полученное в результате суммирования (объединения) системы множеств, соответствует введенному выше понятию универсального множества. При этом в ситуации, когда рассматриваются конечные множества, мощность множества U будет, очевидно, минимальна по сравнению с мощностью любого другого универсального множества системы.

Пересечение (теоретико-множественное произведение) множеств А и В - множество С, состоящее из тех и только тех элементов, которые принадлежат обоим множествам А, В:

С = А 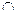В = { x | xÎ A Ù xÎ B },

где 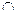– знак умножения (теоретико-множественного произведения), а Ù - логический знак “и”. Произведение множеств А и В довольно часто обозначают А∙В или просто АВ (если это не приводит к недоразумениям; такое, например, возможно, если АВ используется в качестве обозначения одного из рассматриваемых множеств).

Обобщение операции пересечения (умножения) для произвольного числа (системы) множеств S = { A,B,C,…,G }

П = A∙B∙C∙…∙G = { x | xÎ A Ù xÎ B Ù xÎ C Ù…Ù xÎ G }.

В соответствии с определением произведение П = Æ, если система S представляет собой некоторое разбиение.

Разность (теоретико-множественное вычитание) множеств А и В - множество С, состоящее из тех и только тех элементов множества А, которые не содержатся в В:

С = А \ В = { x | xÎ A Ù xÏ B },

где \ - знак теоретико-множественного вычитания. Для операции вычитания вместо А \ В применяют также обозначение А – В. В отличие от двух предыдущих операций разность, во-первых, определена только для двух множеств и, во-вторых, некоммутативна, т.е. А \ В ≠ В \ А.

Применение введенных теоретико-множественных операций для конкретных множеств рассмотрено в примере 1.3.

Дополнение (теоретико-множественное отрицание) множества А – множество

Ā = { xÎ U | xÏ A } = U \ A,

состоящее из тех и только тех элементов, которые не содержатся в A (читается “не А”); в этой формуле U – некоторое известное на момент выполнения операции универсальное множество U.

Особенностью данной операции является то, что хотя она и определена только для одного множества, ее применение требует наличия универсального множества, содержащего в качестве подмножества и само исходное множество А. Так как в соответствии с определением результат операции Ā - также некоторое подмножество универсального множества, причем АĀ = Æ, А+Ā = U, то, следовательно, система S = { A, Ā } будет представлять собой одно из возможных разбиенией универсального множества.

С отмеченной особенностью связан один из хорошо известных приемов решения комбинаторных задач: при решении конкретной задачи, связанной с изучением (исследованием) свойств некоторого множества А, переходят к изучению свойств Ā и далее, используя связь исходного множества и его отрицания, делают вывод о свойствах исходного множества. Ясно, что такой прием применим, если универсальное множество определено однозначно (из всех возможных универсальных множеств выбрано единственное, обладающее минимальной мощностью).

Замечание. В результате применения перечисленных выше теоретико-множественных операций, ориентированных на выполнение четырех действий с множествами (объединение, умножение,, вычитание и дополнение), получаются новые (более сложные с точки зрения определяющих выражений) множества. При этом, меняя порядок (последовательность) операций, могут получаться разные, хотя и эквивалентные выражения. Если универсальное множество U определено, т.е. операция дополнения (отрицания) правомерна, то из выражения, задающего конкретное множество, путем элементарных преобразований, учитывающих связи (соотношения) между различными операциями (см. пример 1.4), любая из первых трех операций может быть исключена (заменена на другие). Чаще всего стараются избавиться от операции вычитания. Для этого используются следующие (рассмотренные в примере 1.4) соотношения (равенства):

, .

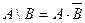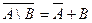Декартово (прямое, геометрическое) произведение множеств А и В - множество D, состоящее из всевозможных упорядоченных пар (a,b), таких, что первый элемент пары берется из множества А, а второй - из множества В:

D = А×В = { (a,b) | aÎ A, bÎ B },

где × - знак декартова произведения.

Эта операция над множествами (в отличие от ранее введенных) изменяет элементы – в новом множестве элементами (объектами) являются пары. Она, очевидно, некоммутативна, так как порядок элементов в паре имеет принципиальное значение (данное свойство характерно для координат вектора на плоскости), т.е. в общем случае А×В ≠ В×А (коммутативность имеет место только в частном случае, когда А = В). Так, например, для A = { a,b,c,d }, B = {1,2,3,4} будет выполняться

А×В = { a 1 ,b 1 ,c 1 ,d 1, a 2 ,b 2 ,c 2 ,d 2, a 3 ,b 3 ,c 3 ,d 3, a 4 ,b 4 ,c 4 ,d 4 },

В×А = { 1 a, 2 a, 3 a, 4 a, 1 b, 2 b, 3 b, 4 b, 1 c, 2 c, 3 c, 4 c, 1 d, 2 d, 3 d, 4 d },

что подтверждает некоммутативность операции.

Обобщение операции декартова произведения для произвольного числа (системы) множеств S = { A,B,C,…,G }:

D = A×B×C×…×G = {(a,b,c,…g) | aÎ A, bÎ B, cÎ C, …,gÎ G },

где d = (a,b,c,…g) – вектор (кортеж, упорядоченный набор), координаты (компоненты)которогоявляются элементами соответствующих множеств из S. Если все множества из S cовпадают (равны А), то декартово произведение называется декартовой степенью множества А и обозначается D = 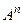, где n - длина кортежа d (размерность системы S). В частном случае, когда n = 2(n = 3), декартово произведение называется квадратом (кубом) множества А.

В качестве простейших примеров геометрического (декартова) произведения (его название связано с именем математика Р. Декарта) могут служить:

координатная плоскость и координатное пространство (декартовы прямоугольные системы координат на плоскости и в трехмерном пространстве) 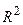= R×R, 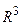= R×R×R;

прямоугольник [ a,b ] × [ c,d ]на плоскости и параллелепипед [ a,b ] × [ c,d ] × [ e,f ] впространстве.

При решении практических задач приходится, как правило, иметь дело не с полным декартовым произведением D, а с некоторым его подмножеством R, элементами которого являются не все кортежи, входящие в D, а только те, которые удовлетворяют определенным условиям (требованиям). Так, например, областью определения (существования) функции двух переменных z = f(x,y) довольно часто является не вся координатная плоскость 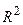, а некоторое подмножество составляющих ее точек.

Всякое подмножество R Í D называется отношением, заданным на множестве D. При этом символом R обозначают как само отношение, так и множество составляющих его кортежей. Последнее иногда называют также графиком отношения или множеством-отношением. Если длина кортежей, входящих в R, равна n, то отношение называют n-местным (n-арным), а величину n - рангом отношения. В ситуациях, когда

R Í D = 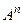, отношениеназываютзаданным на множестве A.

Если некоторый кортеж (a,b,c,…g) Î R, то говорят, что элементы (компоненты) кортежа находятся в отношении R и пишут (a,b,c,…g; R)или R (a,b,c,…g). Иногда вместо слов “находятся в отношении R” говорят “удовлетворяют условию R “.

Алгебра отношений (реляционная алгебра) занимает особое место в теории информационных систем. На ее основе производится, в частности, построение (создание) и сопровождение (ведение) любой реляционной (табличной) базы данных. Каждая поименованная прямоугольная таблица такой базы данных является некоторым отношением, а содержащаяся в ней построчно информация – графиком отношения.

В качестве простейшего примера отношения может быть названа таблица успеваемости группы студентов, в каждой строке которой содержатся кортежи оценок, полученных конкретным студентом в течение определенного периода времени обучения.