Классификация математических моделей

Для теории математического моделирования необходимо знать цель моделирования и представить в математическом виде объект моделирования. Слово «модель» происходит от латинского modus (копия, образ, очертание). Наиболее про­стым и наглядным примером моделирования являются гео­графические и топографические карты. Моделями являются структурные формулы в химии. Модель как средство позна­ния стоит между логическим мышлением и изучаемым про­цессом, явлением.

Моделирование — это замещение некоторого объекта А другим объектом В. Замещаемый объект называется ориги­налом, замещающий — моделью. Таким образом, модель — это заместитель оригинала. В зависимости от цели замеще­ния модель одного и того же оригинала может быть различ­ной. В науке и технике основной целью моделирования яв­ляется изучение оригинала при помощи более простой его модели. Замещение одного объекта другим имеет смысл только в случае их определенного сходства, аналогии.

Математическая модель является приближенным, выраженным в математических терминах, представлением объектов, концепций, систем или процессов. Объекты, кон­цепции, системы или процессы, подлежащие моделирова­нию, называют объектами моделирования (ОМ).

Все объекты и явления в большей или меньшей степени взаимосвязаны, но при моделировании пренебрегают боль­шинством взаимосвязей и объект моделирования рассматри­вают как отдельную систему. Если объект моделирования определен как отдельная система, то необходимо ввести принцип селективности, обеспечивающий выбор требуемых связей с внешней средой. Например, при моделировании электронных схем пренебрегают тепловым, акустическим, оптическим и механическим взаимодействием с внешней средой и рассматривают только электрические переменные. Принцип селективности вводит в систему ошибку, т. е. раз­ницу в поведении модели и объекта моделирования. Сле­дующим важным фактором моделирования является прин­цип причинности, связывающий в системе входные и вы­ходные переменные.

Для количественной оценки системы вводят понятие «состояния». Например, под состоянием электронной схемы понимают значения напряжений и токов в электронной схе­ме в данный момент времени.

При выводе математической модели аналитически чаще всего используются широко известные категории: законы, структуры и параметры.

Если какая-либо переменная величина у зависит от другой переменной х, то первая величина является функцией второй. Эта зависимость записывается в виде у = f(x) или у = у(х). В такой записи переменная х называется аргументом. Важной характеристикой функции является ее производная, процесс нахождения которой называется дифференцированием. Урав­нения, которые по математическим правилам связывают неиз­вестную функцию, ее производные и аргументы, называются дифференциальными. Процесс, обратный дифференцирова­нию, позволяющий по заданной производной найти саму фун­кцию, называется интегрированием.

Рассмотрим частный случай, когда функцией является путь, зависящий от аргумента — времени. Тогда производ­ная пути по времени — это скорость, а производная от ско­рости (или вторая производная от пути) — ускорение. Если йзвестна, например, скорость, то интегрированием находят путь, пройденный телом при движении за определенное вре­мя. Если известно только ускорение, то для нахождения пути операцию интегрирования производят дважды. При этом после вычисления первого интеграла становится изве­стной скорость.

Конечная цель создания математических моделей — установление функциональных зависимостей между пере­менными. Функциональная зависимость для каждой конк­ретной модели может принимать строго определенный вид. Когда моделируется устройство, на вход которого поступает сигнал х_у а на выходе появляется сигнал у, то связь можно записать в виде таблицы. Для этого весь диапазон измене­ния входного и выходного сигналов разбивается на некото­рое число участков. Каждому участку диапазона изменения входного сигнала будет соответствовать определенный учас­ток диапазона изменения выходного сигнала. В сложных си­стемах, где имеется несколько входов и несколько выходов, аналитические зависимости выражаются системами диффе­ренциальных уравнений.

* Законы обычно формулируются для частных областей, Как, например, законы Кирхгофа, Ньютона. Применение этих законов к системе обычно фокусирует наше внимание на единственной области науки и техники. Используя зако­ны Кирхгофа и уравнения Максвелла для анализа электри­ческой системы, исследователь игнорирует другие (напри­мер, тепловые) процессы в системе.

Создание математической модели требует знания присут­ствующих в системе элементов и их взаимосвязей. Парамет­рами математической модели (ММ) являются входящие в системы уравнений различные коэффициенты. Эти ко­эффициенты вместе с уравнениями и граничными условия­ми образуют законченную ММ.

Любую математическую модель можно получить в результате: 1) прямого наблюдения явления, прямого его изучения и осмысливания (модели являются феноменоло­гическими); 2) некоторого процесса дедукции, когда новая модель получается как частный случай из некоторой более общей модели (такие модели называются асимптотически­ми); 3) некоторого процесса индукции, когда новая модель является естественным обобщением элементарных моделей (такие модели называются составными, или моделями ан­самблей).

Все системы существуют во времени и в пространстве. Математически это значит, что время и три пространствен­ные переменные могут рассматриваться в качестве незави­симых переменных.

Существует много признаков классификации математи­ческих моделей по признаку использования тех или иных переменных в качестве независимых, представленных в не­прерывной или дискретной форме; ММ классифицируют следующим образом:

1) модели с распределенными параметрами (все независи­мые переменные берутся в непрерывной форме);

2) модели с сосредоточенными параметрами (все независи­мые пространственные переменные дискретные, а вре­менная переменная непрерывна);

3) модели с дискретными параметрами (все независимые переменные берутся в дискретной форме).

На рис. 3.10, а...ж показана примерная классификация моделей. Все модели можно разделить на вещественные и идеальные (рис. 3.10, а). В данной главе рассматриваются только идеальные модели, которые объективны по своему содержанию (отражая реальную действительность), но субъ­ективны по форме и не могут существовать вне ее. Идеаль­ные модели существуют лишь в познании людей и функцио­нируют по законам логики. К логическим моделям относят­ся различные знаковые модели. Существенным моментом создания любой знаковой модели является процедура фор­мализации (формулы, алфавит, системы счислений).

В настоящее время в ряде областей науки и техники по­нятие модели трактуется не в духе классической физики, как наглядная, например, механическая система, а в духе современного этапа познания как абстрактная логико-мате­матическая структура.

В современном моделировании наряду с возрастанием в познании роли абстрактно-логических моделей существует другая тенденция, связанная с широким применением ки­бернетических функционально-информационных моделей.

Своеобразие кибернетического моделирования состоит в том, что объективное сходство модели и моделируемого объ­екта касается только их функций, областей применения, связи с внешней средой. Основа информационного подхода к изучению кибернетических процессов — абстрагирование.

Рассмотрим модели, которые имеют место в САПР БИС: структурные, функциональные, геометрические, знаковые, мысленные, аналитические, численные и имитационные.

Структурные модели воспроизводят состав элементов объекта или системы, их расположение в пространстве и взаимосвязи, т. е. структуру системы. Структурные модели могут быть и вещественными (макеты), и идеальными (на- | пример, машиностроительные чертежи, топология печатной | платы и топология ИС).

Функциональные модели имитируют только способ пове­дения оригинала, его функциональную зависимость от внешней среды. Наиболее характерным примером служат модели, построенные на концепции «черного ящика».

В этих моделях удается воспроизвести функционирование £ оригинала, полностью отвлекаясь от его содержимого и структуры, связывая с помощью математического соотношения различные входные и выходные величины.

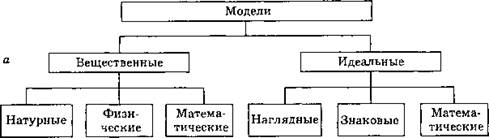
Рис. 3.10. Общая классификация моделей (а), а также моделей натурных (б), физических (в), вещественных математических (г), наглядных (д), знаковых (е), идеальных математических (ж)

Геометрические модели отражают только структуру объ­екта и имеют большое значение в связи с проектированием электронных систем. Эти модели, построенные на основе геометрического подобия, позволяют решать задачи, связан­ные с оптимальным размещением объектов, прокладкой трасс на печатных платах и интегральных схемах.

Знаковые модели представляют собой упорядоченную за­пись символов (знаков). Знаки взаимодействуют между со­бой не по физическим законам, а по правилам, установлен­ным в той или иной области знаний, или, как принято гово­рить, согласно природе знаков. Знаковые модели имеют в настоящее время чрезвычайно широкое распространение. Практически каждая область знаний — лингвистика, про­граммирование, электроника и многие другие — выработала свою символику для описания моделей. Таковыми являются программы, схемы и т. п.

Мысленные модели являются продуктом чувственного восприятия и деятельности абстрактного мышления. К мысленным моделям можно отнести известную планетар­ную модель атома Бора. Для передачи этих моделей их пред­ставляют в виде словесного или знакового описания, т. е. мысленные модели могут фиксироваться в виде различных знаковых систем.

Аналитические модели позволяют получить явные зави­симости необходимых величин от параметров и перемен­ных, характеризующих изучаемое явление. Аналитическое решение математического соотношения является обобщен­ным описанием объекта

Численные модели характеризуются тем, что значения необходимых величин можно получить в результате приме­нения соответствующих численных методов. Все численные методы позволяют получить только частную информацию относительно искомых величин, поскольку для своей реали­зации требуют задания конкретных значений всех парамет­ров, входящих в математическое соотношение. Для каждой искомой величины приходится по-своему преобразовывать математическую модель и применять соответствующую чис­ленную процедуру.

Имитационные модели реализуются на ЭВМ в виде мо­делирующих алгоритмов (программ), позволяющих вычис­лять значения выходных переменных и определять новое состояние, в которое переходит модель при заданных значе­ниях входных переменных, параметров и исходного состоя­ния модели. Имитационное моделирование в отличие от численного характеризуется независимостью моделирую­щего алгоритма от типа информации, которую необходимо получить в результате моделирования. Достаточно универ­сальной, гибкой и эффективной является математическая модель, которая представляется в абстрактной математиче­ской форме посредством переменных, параметров, уравне­ний и неравенств.

В ММ входят следующие элементы: переменные (зависи­мые и независимые); константы или фиксированные пара­метры (определяющие степень связи переменных между со­бой); математические выражения (уравнения или/и нера­венства, объединяющие между собой переменные и параметры); логические выражения (определяющие различ­ные ограничения в математической модели); информация (алфавитно-цифровая и графическая).

Математические модели классифицируют по следующим критериям: 1) поведению моделей во времени; 2) видам входной информации, параметров и выражений, составляю­щих математическую модель; 3) структуре математической модели; 4) типу используемого математического аппарата.

Применительно к интегральным схемам можно предло­жить следующую классификацию.

В зависимости от характера свойств интегральной схемы математические модели делятся на функциональные и струк­турные.

Функциональные модели отображают процессы функци­онирования объекта, эти модели имеют форму систем урав­нений.

При решении ряда задач проектирования широкое при­менение находят математические модели, отображающие только структурные свойства проектируемого объекта; та­кие структурные модели могут иметь форму матриц, гра­фов, списков векторов и выражать взаимное расположение элементов в пространстве, наличие непосредственной связи в виде проводников и т. д. Структурные модели используют в том случае, когда задачи структурного синтеза удается формализовать и решать, абстрагируясь от особенности фи­зических процессов в объекте.

Пример:

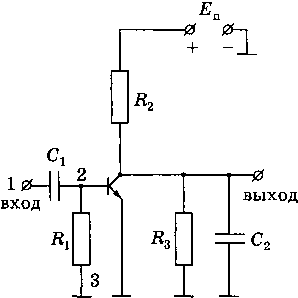
Рис. 3.11. Структурная модель инвертора 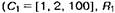= [2, 3, 5] ит. д.)

По методу получения функциональные математические модели делятся на теоретические и формальные.

Теоретические модели получаются на основе изучения физических закономерностей, причем структура уравнений и параметры моделей имеют четкое физическое обоснование.

Формальные модели получаются при рассмотрении свойств реального объекта как черного ящика.

Теоретический подход позволяет получать более универ­сальные модели справедливые для различных режимов ра­боты и для широких диапазонов изменения внешних пара­метров.

Ряд признаков в классификации связан с особенностями уравнений, составляющих математическую модель; в зави­симости от линейности или нелинейности уравнений модели делят на линейные и нелинейные.

В зависимости от мощности множества значений пере­менных модели делят на непрерывные и дискретные (рис. 3.12).

В непрерывных моделях фигурирующая в них перемен­ная непрерывна или кусочно-непрерывна.

Переменные в дискретных моделях — дискретные вели­чины, множество которых счетно.

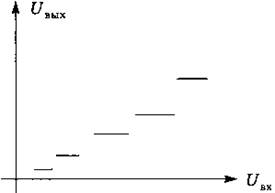
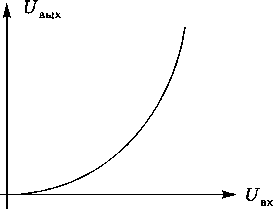
Рис. 3.12. Непрерывные и дискретные переменные

По форме связи между выходными, внутренними и внешними параметрами различают модели в виде систем уравнений и модели в виде явной зависимости выходных па­раметров от внутренних и внешних. Первые из них называ­ются алгоритмическими, а вторые — аналитическими.

В зависимости от того, учитывают ли уравнения модели инерционность процессов в объекте проектирования, разли­чают модели динамические и статические.