Рассмотрим неоднородное квазилинейное уравнение (3). Сведём поиск решения неоднородного уравнения к задаче о нахождении решения однородного уравнения, то есть к неизвестной ситуации. Для этого введём в рассмотрение новую функцию 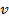 , положив
, положив 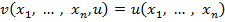 - решение данного квазилинейного уравнения (3). Определённая таким образом функция тождественно равна нулю. Однако
- решение данного квазилинейного уравнения (3). Определённая таким образом функция тождественно равна нулю. Однако 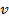 должна удовлетворять уравнению:
должна удовлетворять уравнению:
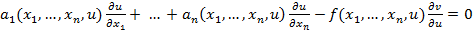 .
.
Обозначив 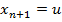 ,
, 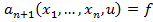 предыдущее уравнение можно записать в виде, аналогичном (4). Таким образом, считаем задачу решённой.
предыдущее уравнение можно записать в виде, аналогичном (4). Таким образом, считаем задачу решённой.
Значит соответствующая неоднородному уравнению характеристическая система имеет вид:
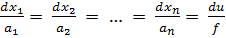 . (8)
. (8)
Помня предыдущее, утверждаем, что система (8) имеет ровно n независимых первых интегралов 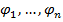 . Общее решение (3) записывается аналогично (7), то есть как
. Общее решение (3) записывается аналогично (7), то есть как
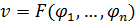 ,
,
где 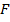 - произвольная непрерывно дифференцируемая функция от
- произвольная непрерывно дифференцируемая функция от 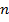 независимых первых интегралов. Поскольку
независимых первых интегралов. Поскольку 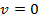 по определению, то общее решение квазилинейного уравнения (3) получили в неявном виде:
по определению, то общее решение квазилинейного уравнения (3) получили в неявном виде:
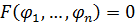 . (9)
. (9)
В частности, если 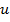 входит только в один из первых интегралов, например, в последний, то общее решение можно записать в явном, разрешённом относительно искомой функции
входит только в один из первых интегралов, например, в последний, то общее решение можно записать в явном, разрешённом относительно искомой функции 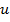 , в виде
, в виде
|
|
|
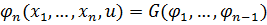 ,
,
где 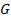 - произвольная непрерывно дифференцируемая функция.
- произвольная непрерывно дифференцируемая функция.
Замечание. При решении систем (5) или (8) полезно использовать свойство равных дробей: если имеются равные дроби 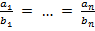 и произвольные
и произвольные 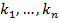 , то из равенства
, то из равенства
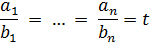
будет следовать равенство
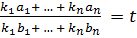 .
.
Также часто используются следующие формулы:
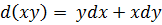 ,
, 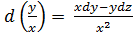 ,
,
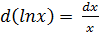 ,
, 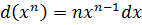 .
.
Пример 1. Найти общее решение уравнения
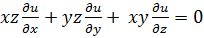 .
.
Решение.
Данное уравнение является линейным однородным уравнением. Выписываем соответствующую характеристическую систему:
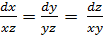 .
.
Мы должны найти два линейно независимых первых интеграла. Ищем две интегрируемые комбинации[1]. Из первого уравнения характеристической системы 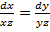 , то есть
, то есть 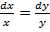 находим один из первых интегралов
находим один из первых интегралов 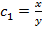 .
.
Пользуясь свойством равных дробей, составим вторую интегрируемую комбинацию: умножим числитель и знаменатель первых двух соотношений на 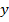 и
и  соответственно и сложив их, получим
соответственно и сложив их, получим 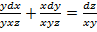 или
или 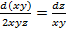 .
.
Сокращая обе части последнего уравнения на 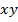 и интегрируя его, получим второй из первых интегралов
и интегрируя его, получим второй из первых интегралов 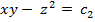 . Поскольку найденные первые интегралы независимы (проверить самостоятельно), то общее решение данного уравнения имеет вид
. Поскольку найденные первые интегралы независимы (проверить самостоятельно), то общее решение данного уравнения имеет вид
 ,
,
где 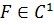 .
.
Пример 2. Решить уравнение
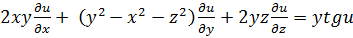 .
.
Решение.
Данное уравнение является квазилинейным. Характеристическая система, ему соответствующая, имеет вид:
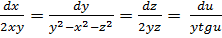 .
.
Нужно найти три интегрируемые комбинации. Приравнивая первое и третье соотношения и сокращая на 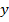 , получим уравнение
, получим уравнение 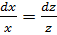 , откуда находим
, откуда находим 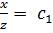 .
.
Для нахождения второго семейства характеристик используем свойство равных дробей. Умножим числитель и знаменатель первых трёх соотношений соответственно на 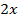 ,
, 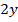 ,
, 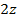 и, сложив их, получим:
и, сложив их, получим:
|
|
|
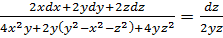 .
.
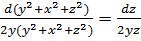 . Собрав дифференциалы элементарных функций, будем иметь:
. Собрав дифференциалы элементарных функций, будем иметь:
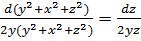 или
или 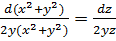 .
.
Интегрируя, найдём ещё один первый интеграл системы
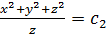 .
.
Приравнивая третье и четвёртое соотношения и сокращая на 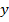 , получим
, получим 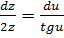 , откуда
, откуда
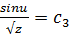 .
.
Значит, решение исходного уравнения выписывается неявно в виде
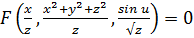 .
.
Заметим, что неизвестная функция 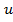 входит только в один первый интеграл, и поэтому общее решение также можно записать как
входит только в один первый интеграл, и поэтому общее решение также можно записать как
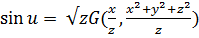 .
.
 2015-07-21
2015-07-21 2405
2405
