Линейные дифференциальные уравнения с частными производными второго порядка

Будем рассматривать функцию двух переменных 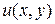. Для обозначения частных производных будем использовать нижние индексы:

, , , , , …..

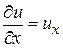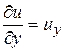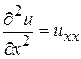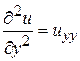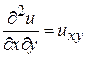Линейным дифференциальным уравнением 2-го порядка с частными производными для функции двух переменных 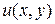называется уравнение вида:

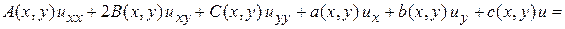
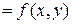, (1)

где 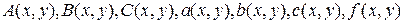– функции двух переменных 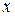и 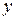, заданные в некоторой области 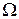плоскости .

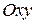Если 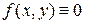, то уравнение называется однородным, в противном случае – неоднородным.

Введем обозначение

,

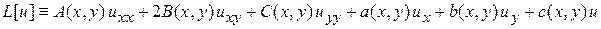здесь 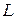– линейный дифференциальный оператор, определенный на линейном пространстве 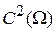функций 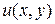. Оператор 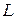называют линейным, если, при вещественных ,

.

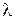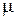
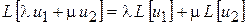Соответствующее однородное уравнение запишется в виде:

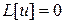. (2)

Свойства решений линейного однородного дифференциального уравнения с частными производными:

1. Если 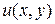есть решение уравнения (2), то и 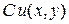, где 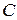– постоянная, есть также решение уравнения (2).

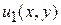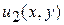2. Если и есть решения уравнения (2), то сумма 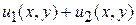есть также решение уравнения (2).

Доказательство свойств следует из линейности оператора .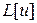

Следствие из 1 и 2: Если функции 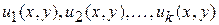есть решения уравнения (3), то и их линейная комбинация

,

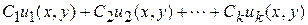где 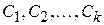– произвольные постоянные, также является решением уравнения (2), но, в отличие от обыкновенного линейного дифференциального уравнения, уравнение в частных производных может иметь бесконечное множество линейно независимых частных решений.

Неоднородное уравнение можно записать в виде:

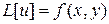. (3)

Свойства решений линейного неоднородного дифференциального уравнения с частными производными:

1. Если 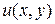есть решение уравнения (2), а функция 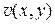есть решение соответствующего однородного уравнения (1), то сумма 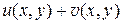есть также решение неоднородного уравнения (1).

2. Если 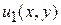есть решение уравнения 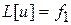и 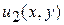есть решения уравнения 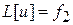, то сумма 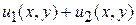есть также решение уравнения .

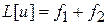Покажем, что любое уравнение (1) может быть приведено к одному из трех видов.

Составим из коэффициентов уравнения (1) обыкновенное дифференциальное уравнение 1-го порядка:

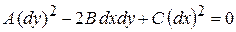, (4)

которое называется характеристическим уравнением для уравнения (1).

Уравнение (4) распадается на два дифференциальных уравнения:

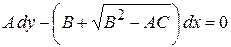(5)

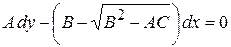(6)

(если перемножим уравнения (5) и (6), то получим уравнение (4)).

Из (5) и (6) следует

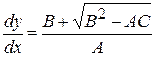(5’)

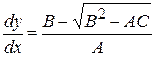. (6’)

Общие интегралы (общие решения) этих уравнений называются характеристиками уравнения.

1. Если при всех допустимых 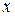и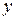

,

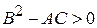Тогда общие решения уравнений (5’) и (6’) различны и вещественны

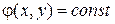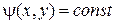и , (7)

т.е. имеем два различных вещественных семейства характеристик уравнения (1);

2. Если при всех допустимых 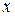и ,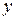

,

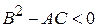уравнение (1) называется уравнением эллиптического вида.

Общие интегралы характеристического уравнения (4) будут комплексно сопряженные функции

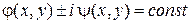(7’)

и получим два семейства мнимых характеристик;

3. Если при всех допустимых 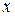и ,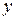

,

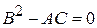уравнение (1) называется уравнением параболического вида.

Тогда уравнения (5’) и (4’) совпадают и мы получаем один общий вещественный интеграл

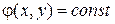, (7”)

и одно семейство характеристик.

Пример.

Определим тип уравнения и найдем характеристики

.

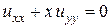Здесь 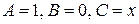и .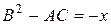

Таким образом,

1) если 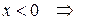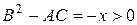и уравнение принадлежит к гиперболическому виду;

Решаем характеристические уравнения

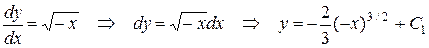и первый общий интеграл имеет вид

, .

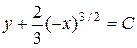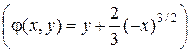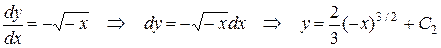и второй общий интеграл имеет вид

, .

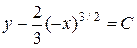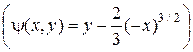2) если 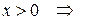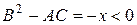и уравнение принадлежит к эллиптическому виду;

Составим характеристическое уравнение и запишем его в виде

, ,

.

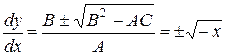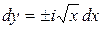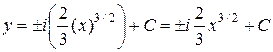Таким образом, общий интеграл уравнения представляет собой комплексно-сопряженные функции

,

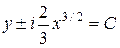здесь 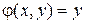– вещественная часть, 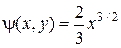– мнимая часть.

3) если 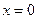, то уравнение принадлежит к параболическому типу;

Составим характеристическое уравнение .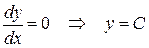

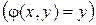Канонические формы для уравнений (1)

А) Пусть уравнение (1) принадлежит к гиперболическому виду, тогда вводя новые переменные

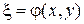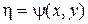и (8)

уравнение (1) можно привести к виду

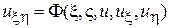. (9)

Уравнение (9) – первая каноническая форма уравнений гиперболического типа.

Часто уравнение (1) приводят ко второй канонической форме:

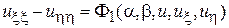(9’)

Б) Пусть уравнение (1) принадлежит к эллиптическому виду, тогда вводя новые переменные

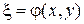и ,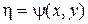

здесь 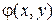– вещественная часть решения (7’), 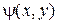– мнимая часть решения (5’), уравнение (1) можно привести к виду

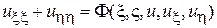(10)

– каноническая форма для уравнений эллиптического типа.

В) Пусть уравнение (1) принадлежит к параболическому виду, тогда вводим новые переменные

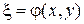и ,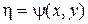

здесь 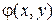– общий интеграл уравнения (3’), а функция 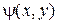– произвольная функция, удовлетворяющая условиям 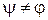и .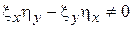

После замены переменных уравнение (1) перейдет в следующее

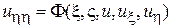, (11)

– каноническая форма для уравнений параболического типа.