Ортогональные операторы и их матрицы

В евклидовом пространстве важную роль играют ортогональные операторы.

Определение 11.4. Линейный оператор A, действующий в действительном n -мерном евклидовом пространстве V, называется ортогональным, если

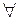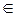(Ax, Ay) = (x, y), x, y V.

Таким образом, ортогональный оператор сохраняет скалярное произведение, а значит, он сохраняет длины векторов и углы между ними. В частности, если x и y – ортогональные векторы, то Ax и Ay – также ортогональные векторы.

Отсюда можно сделать вывод, что если u ¹, u ²,…, u ⁿ – ортонормированный базис евклидова пространства V, то Au ¹, Au ²,…, Au ⁿ также является ортонормированным базисом пространства V.

Верно и обратное: линейный оператор A, переводящий один ортонормированный базис в другой ортонормированный базис, ортогонален. Действительно, пусть ортонормированный базис u ¹, u ²,…, u ⁿ оператором A переводится в ортонормированный базис v ¹, v ²,…, v ⁿ, т. е. Au ⁱ = v ⁱ, i = 1, 2,..., n. Тогда если x = x ₁ u ¹ + x ₂ u ² +…+ x_n u ⁿ и y = у ₁ u ¹ + у ₂ u ² +…+ у_n u ⁿ, то Ax = x ₁ Au ¹ + x ₂ Au ² +… … + x_n A u ⁿ = x ₁ v ¹ + x ₂ v ² +…+ x_n v ⁿ и, аналогично, Ay = у ₁ v ¹ + у ₂ v ² +…+ у_n v ⁿ. Отсюда (Ax, Ay) = x ₁ у ₁ + x ₂ у ₂ +... + x_nу_n = (x, y), т. к. в ортонормированном базисе скалярное произведение векторов равно сумме произведений их одноименных координат.

Пусть A – ортогональный оператор и A ^* – ему сопряженный. Тогда

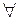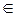(x, y) = (Ax, Ay) = (x, A ^*(Ay)) = (x, (A ^* A) y), x, y V.

Значит, A ^* A = Е. Аналогично можно убедиться в том, что и AA ^* = Е.

Таким образом, для ортогонального оператора имеет место равенство

A ^* A = AA ^* = Е. (11.3)

Следовательно, если A – ортогональный оператор, то сопряженный ему оператор A ^* удовлетворяет равенству

A ^* = A ^–1. (11.4)

Равенство (11.4) является необходимым и достаточным условием того, чтобы оператор A был ортогональным. Отсюда, в частности, следует, что ортогональный оператор всегда невырожден.

Перечислим простейшие свойства ортогональных операторов.

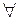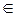1°. Тождественный оператор Е является ортогональным, т. к. из равенств Еx = x и Еy = y следует равенство (Еx, Еy) = (x, y), x, y V.

2°. Произведение ортогональных операторов является ортогональным оператором. Это следует из равенств

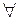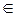((AB) x, (AB) y) = (A (Bx), A (By)) = (Bx, By) = (x, y), x, y V,

если A и B – ортогональные операторы.

3°. Оператор, обратный ортогональному, является ортогональным оператором. В самом деле, если A ^* = A ^–1, то в силу свойства 6° сопряженных операторов (A ^–1)^* = (A ^*)^–1 = (A ^–1)^–1 = A.

Другими словами, свойство 3° означает, что оператор A переводит произвольный ортонормированный базис u ¹, u ²,…, u ⁿ в ортонормированный базис Au ¹, Au ²,…, Au ⁿ, а оператор A ^–1 восстанавливает исходный ортонормированный базис.

4°. Если A – ортогональный оператор, то произведение a A будет ортогональным в том и только в том случае, если a = ±1. Это следует из равенства ((a A) x, (a A) y) = a ²(Ax, Ay) = a ²(x, y).

Выясним теперь структуру матрицы A = 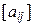, i, j = 1, 2,..., n, ортогонального оператора A в некотором ортонормированном базисе. Очевидно, соответствующие условиям (11.3) и (11.4) матричные равенства имеют вид

A ^* A = AA ^* = Е; (11.5)

A ^* = A ^–1. (11.6)

Определение 11.5. Матрица А, для которой справедливо равенство (11.6), называется ортогональной матрицей.

Из матричного равенства (11.5) с учетом правила умножения матриц получаем

;

;

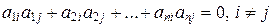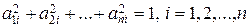и

;

.

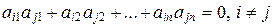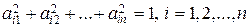Таким образом, столбцы (строки) ортогональной матрицы, рассматриваемые как векторы-столбцы (векторы-строки), сами образуют ортонормированную систему.

Итак, в любом ортонормированном базисе матрица ортогонального преобразования является ортогональной.

Пример 2. Матрица

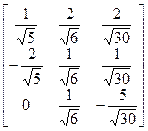
является, очевидно, ортогональной, т. к. для ее элементов условия ортогональности выполнены.·

В заключение выясним геометрический смысл ортогонального оператора в R ¹и R ².

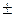В случае пространства R ¹ базисный вектор е ортогональным оператором A переводится в вектор Aе R ¹. Следовательно, Aе = l е, где l = (свойство 4°), т. е. Aе = е. А это означает, что A – либо тождественный оператор (Aе = е), либо центральная симметрия (Aе = – е).

В пространстве R ² каждый ортогональный оператор в некотором ортонормированном базисе определяется ортогональной матрицей

A = .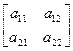

Тогда 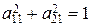, , 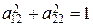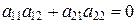. Первые два равенства означают, что найдутся такие j и y, что 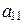= cos j, 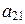= sin j, 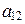= cos y и 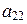= sin y, а из третьего получаем, что cos j cos y + sin j sin y = cos(j – y) = 0, откуда вытекает:

1) y – j = 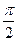или 2) y – j = 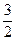p.

В первом случае 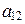= cos y = – sin j, 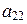= sin y = cos j и тогда

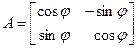= А ₁.

То есть А ₁ – поворот на угол j вокруг начала координат (тождественный оператор при j = 0 и центральная симметрия относительно начала координат при j = p).

Во втором случае = sin j, = – cos j и

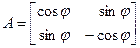= А ₂.

Нетрудно видеть, что матрицу А ₂ можно представить в виде произведения двух матриц, т. е.

А ₂ .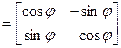

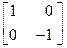Здесь левая матрица в правой части равенства – матрица поворота плоскости на угол j, а вторая – матрица зеркального отражения относительно оси Ox. Таким образом, матрица А ₂ есть матрица оператора, осуществляющего зеркальное отражение векторов относительно оси Ox с последующим поворотом их на угол j вокруг начала координат.