Задачи многокритериальной оптимизации

В большинстве случаев абсолютно лучшее решение выбрать невозможно, так как при переходе от одного варианта к другому (например, от P_A к P_B) улучшаются одни критерии (на рис.7а — К₂), но ухудшаются другие (К₁). Состав таких критериев называется противоречивым, и окончательно выбранное решение всегда будет компромиссным.

Компромисс разрешается введением тех или иных дополнительных ограничений или субъективных предположений. Поэтому невозможно говорить об объективном единственном решении такой задачи.

В задачах многокритериальной оптимизации поиск решений возможен рядом способов.

Выделение области компромиссов и отбрасывание заведомо неудовлетворительных решений.

Множество допустимых решений М_д(к) разделяется на множество худших М_х(к) и множество нехудших М_нх(к) решений. Худшим считается такое решение, если можно найти другое решение, значения критериев у которого не хуже (такие же) или лучше, чем у рассматриваемого. Решение, для которого из множества допустимых решений нельзя найти ни одного лучшего по всем критериям, называется нехудшим. Так, для множества, представленного на рис. 7а: множество худших решений М_х(к)={ P_D, P_E } и множество нехудших решений М_нх(к)={P_A, P_B, P_C }, поскольку, например, у решения P_B ={К_1В, К_2в} значения всех критериев лучше, чем у решения P_D ={К_1D, К_2D}. С другой стороны, решение P_А по сравнению с решением P_В лучше по критерию К₁, но хуже по критерию К₂.

Пусть К₁ — стоимость изделия в рублях, К₂ — масса этого же изделия в килограммах.

Имеется три варианта решений: P ₁={4, 4}, P₂={8, 1}, P ₃={7, 6}. Очевидно, что решение P₁ лучше решения P₃ по всем критериям и без ущерба решение P₃ можно отбросить.

Выбрать лучшее из решений P₁ и P₂ затруднительно: по стоимости выгоднее первое решение, а по массе — второе.

Графически множество нехудших решений соответствует части граничных точек множества допустимых решений, которые находятся между точками касания линий, параллельных осям координат (при условии, что критерии убывают с улучшением решения). На рис.7б — это точки отрезка АВСБ границы области Мд(к). В пространстве параметров множество нехудших решений уже не обязательно будет лежать на границе множества допустимых решений М_х(к), а распределяется по всему пространству.

Множество нехудших решений еще называют неулучшаемым: замена одного решения из этого множества на другое ведет к улучшению одних критериев и обязательному ухудшению других.

Математический алгоритм выбора нехудших решений основан на использовании бинарных отношений предпочтения теории принятия решений. Смысл бинарных отношений заключается в последовательном попарном сравнении элементов в соответствии с установленным правилом предпочтения. Так, предпочтительность решения P_D по отношению к решению P_E (рис.7а) условно записывается как P_D R P_E или P_D > P_E. Обычно для поиска множества нехудших решений используют отношения предпочтения Слейтера или Парето, последние — чаще. Математическая запись отношений предпочтения Парето (фамилия итальянского ученого-экономиста, введшего в начале 20-х годов 20-го века это понятие) имеет вид: P_D P P_E, т.е. решение P_D ={К_1D,..., К_mD} лучше решения P_E ={К_1Е,..., К_mЕ} только тогда, когда К_iD ≤ К_iЕ (i=1,...,m), причем хотя бы для одной сравниваемой пары критериев (например, при i= l) имеет место строгое неравенство К_1D < К_1Е. Множеству Слейтера (области Слейтера) графически соответствует отрезок ABCD на рис.7б, в состав которого входит горизонтальный участок BC, а множеству Парето (области Парето) — участки AB и CD.

Область Парето — это область компромиссов: все решения здесь равнозначны, а окончательный выбор решения связан с введением дополнительного условия, часто — субъективного характера. Поиск решений, оптимальных по Парето, позволяет объективно сократить область возможного выбора, причем наибольшее усечение области допустимых решений достигается при назначении двух критериев. При увеличении числа критериев эффективность этого метода падает. Целесообразен одновременный учет 2...5 критериев.

Замена критериев ограничениями и последующий поиск решений в области, задаваемой этими и ранее заданными ограничениями.

Например, задачу минимизации массы и потерь энергии изделия можно свести к задаче проектирования изделия, у которого потери не превысят, допустим, 5%, а масса — 10 кг. Если в полученной области будет находиться несколько решений, то ограничения можно ужесточить (скажем, ограничить предельную массу 6 кг). Если же решений нет, то ограничения смягчают.

Сложность такой задачи — в удачной ее постановке, т.е. в быстром усечении области до одного решения при минимальном влиянии субъективных факторов, связанном с выбором ограничений. Введение ограничений (например, К₁¹ и К₂¹ в пространстве двух показателей качества, рис.7а) соответствует выделению прямоугольной области, и очевидно, что лучшим решением будет оказываться одно из нехудших (из области Парето).

Сведение задачи к однокритериальной и последующее ее решение методами скалярной оптимизации.

Такое сведение осуществляется на основе введения дополнительных предположений о взаимосвязи и взаимозависимости учитываемых в задаче показателей качества. Выбор конкретного способа сведения зависит от многих обстоятельств, таких как квалификация специалистов, объем и достоверность имеющейся в их распоряжении информации, срочность решения, степень ответственности за получаемый результат. При этом следует учитывать, что характер решения меняется и со временем (то, что выгодно сегодня, может быть разорительным завтра).

Сведение задачи к однокритериальной проводится посредством выбора одного критерия из нескольких, введения общей единицы измерения для всех критериев, свертки нескольких критериев в один и другими методами.

- Выбор из рассматриваемого перечня критериев одного, главного, который отражает наиболее существенные свойства исследуемого объекта. Выбор основывается на опыте разработчика или на мнении экспертов. С оставшимися критериями поступают следующими способами:

· заменяют их ограничениями, которые при необходимости ужесточают или смягчают;

· ранжируют критерии, т.е. упорядочено располагают по степени важности характеризуемых свойств. Например, К₁> К₃ >(К₂, К₅) > K₄..., что означает, что критерий К₁ важнее всех остальных (главный), из которых более важный — К₃, из оставшихся критериев более важны К₂, К₅, в свою очередь, равноценные друг другу, и т.д. Далее выбирают решение при главном критерии, вводя пороговые ограничения на остальные или же вообще их не учитывая. Если решений оказывается несколько, то лучшее из них выбирают на основе второго по важности критерия из ранжированного ряда, и т.д.

- Введение общей единицы измерения критериев. В качестве такой меры часто выбирают стоимость достижения того или иного уровня качества, будь то снижение массы и потерь энергии, современный дизайн и т.д. Т.е. для каждого варианта объекта, характеризуемого своим уровнем качества, подсчитывают (или оценивают), с одной стороны, расходы на производство, эксплуатацию и утилизацию, а с другой стороны — доходы от использования. По величине экономической эффективности (разности доходов и расходов) делают вывод о предпочтительности вариантов.

- Свертка векторного критерия, т.е. замена рассматриваемых критериев одним новым, называемым функцией полезности или целевой функцией. Выбор целевой функции сложная задача:

· нужно числено оценить, а не только ранжировать каждый критерий;

· нужно объединить критерии, которые имеют, как правило, разную размерность (например, рубли, килограммы, проценты и т.д.);

· нужно объединить критерии, величины и диапазоны изменения которых могут существенно разниться (например, потери измеряются сотыми долями, что несравнимо меньше величины, допустим, массы, измеряемой десятками и сотнями килограммов);

· сложно, а иногда и невозможно найти численную меру показателя качества. Например, такие неформализуемые показатели, как степень красоты, удобство работы;

· величины разных критериев могут определяться с различной достоверностью. Так, например, если масса изделия оценивается достаточно точно, то надежность задается заметно грубее.

· Грамотное выполнение свертки с получением максимально достоверного результата достигается тщательным проведением предварительных исследований, привлечением знаний и опыта специалистов-экспертов. Методы постановки задач векторной оптимизации подробно изложены в книге Кини Р. Л. и Райфа Х.

· В качестве целевой функции f часто используют:

· аддитивную функцию, т.е. функцию, подсчитываемую для каждого варианта (j = 1,..., n) решения как сумму отдельных критериев (i = 1,..., m) с учетом их относительной важности λ_i, т.е. f j = Σλ_i·К_ij. Коэффициент &lambda_i называется весовым. Обычно принимают Σλ_i = 1;

· мультипликативную функцию, т.е. функцию, подсчитываемую как произведение отдельных критериев с соответствующими степенями λ_i, т.е. f _j = П(К_ij) ^λi.

В пределах решения одной задачи должен соблюдаться единый подход к подсчету целевой функции.

Рассмотрим такой показатель качества как компактность. Под ним обычно понимается совокупность минимизируемых критериев — габаритных размеров, допустим x,y,z. Тогда целевой функции компактности в аддитивной формулировке f _a=x+y+z будет соответствовать периметр, а в мультипликативной — f _м=xyz, т.е. объем.

Чаще используется аддитивная целевая функция, поскольку ее применение позволяет применять более простой и хорошо разработанный математический аппарат линейного программирования.

Входящие в целевую функцию отдельные критерии обязательно нормируют, т.е. приводят к безразмерному виду и устанавливают интервалы изменения от 0 до 1. Назначение величин весовых коэффициентов обычно проводят методом экспертных оценок. Для этого суммируют (с учетом опыта и квалификации) индивидуальные оценки каждого из группы экспертов. Учет многих мнений позволяет снизить влияние эвристичности решений и волевого подхода отдельных экспертов.

Применение различных подходов (что видно из примера) может приводить к разным результатам. Это еще раз подчеркивает важность в задачах многокритериальной оптимизации тщательности формулировок и подготовки данных, строгого обоснования вводимых предположений.

Графически в пространстве показателей качества применение целевой функции означает поиск точки касания N границы множества допустимых решений с линией, задаваемой этой функцией, при параллельном ее смещении от начала координат (если функция цели минимизируется) или из бесконечности к началу координат (если функция максимизируется). На рис. 8 сказанное поясняется на примере двухкритериальной задачи с непрерывным множеством допустимых решений М_д(к).

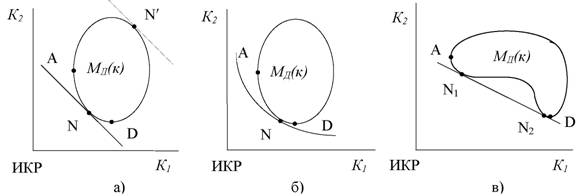
Рис. 8. Положение оптимального решения N при свертке векторного критерия

Аддитивной целевой функции соответствует прямая линия (рис. 8а), угол наклона которой определяется соотношением величин весовых коэффициентов и способом нормирования критериев. Оптимальному решению соответствует точка касания N, если функция цели минимизируется, и точка N' — если максимизируется. Положение точки касания при изменении угла наклона может меняться в пределах дуги АD множества Парето, т.е. оптимальное решение является одним из решений из множества Парето.

Мультипликативной целевой функции соответствует кривая линия (рис.8б, принято, что функция цели минимизируется), форма которой определяется соотношением величин весовых коэффициентов и способом нормирования критериев.

Решения, соответствующие точкам A и D, получаются в случае ранжирования критериев и последующего рассмотрения только одного из них.

В некоторых случаях, если область нехудших решений ограничена извилистой линией, поиск с помощью функции цели может дать нескольких оптимальных решений (рис.8в).

Недопустима свертка показателей безопасности или их отбрасывание при ранжировании.