1.1. Степень с натуральным показателем.
Если 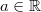 ,
, 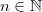 , то величина
, то величина 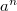 определяется так.
определяется так.
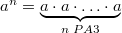
1.2. Степень с целым показателем.
Если 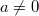 , то по определению считается, что
, то по определению считается, что 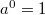 (
(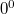 не определен).
не определен).
Если 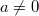 ,
, 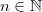 , то величина
, то величина 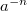
определяется так.
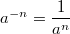
1.3. Степень с рациональным показателем.
Если 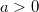 ,
, 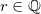 , то величина
, то величина 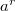 определяется так.
определяется так.
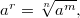
где 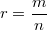 ,
, 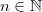 ,
, 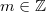
Замечание. В рациональную степень можно возводить только положительные числа!
1.4. Степень с иррациональным показателем.
Строгого определения степени с иррациональным показателем на школьном уровне дать нельзя. Для этого нужно хорошо понимать что такое предел последовательности, и как с ним работать. Но основываясь на интуитивном представлении о пределе можно сказать следующее.
Пусть даны положительное число  , и иррациональное число
, и иррациональное число  . Рассмотрим какую-нибудь последовательность
. Рассмотрим какую-нибудь последовательность 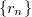 рациональных чисел, стремящихся к
рациональных чисел, стремящихся к  (например, его десятичные приближения). Тогда предел последовательности
(например, его десятичные приближения). Тогда предел последовательности 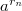 (это уже рациональная степень числа
(это уже рациональная степень числа  ) будем называть
) будем называть  -той степенью числа
-той степенью числа  , и обозначать
, и обозначать 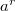 .
.
Четкое определение, что такое предел последовательности, почему существует предел 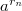 , и почему он не зависит от выбора приближающей последовательности
, и почему он не зависит от выбора приближающей последовательности 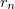 , будет рассказано в институте, в рамках курса математического анализа.
, будет рассказано в институте, в рамках курса математического анализа.
1.5. Свойства степени с действительным показателем.
Для любых действительных 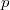 ,
, 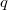 и произвольных
и произвольных 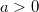 ,
, 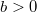 имеют место следующие равенства.
имеют место следующие равенства.
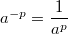
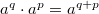
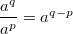
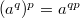
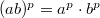
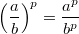
2. Логарифм.
Логарифмом числа  по основанию
по основанию  (где
(где 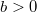 ,
, 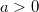 ,
, 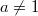 ) - это степень, в которую нужно возвести число
) - это степень, в которую нужно возвести число  , чтобы получилось число
, чтобы получилось число  . Обозначается
. Обозначается 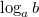 .
.
1.1. Основное логарифмическое тождество.
Из определения логарифма следует тождество.
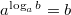
1.2. Свойства логарифмов.
Если 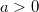 ,
, 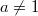 ,
, 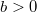 ,
, 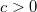 ,
, 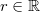 , то
, то
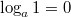 ,
,
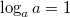 ,
,
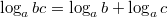 ,
,
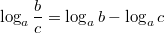 ,
,
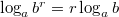 ,
,
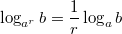 .
.
Поэтому
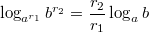 .
.
В частности,
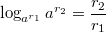 .
.
1.3. Формула перехода к новому основанию.
Если 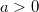 ,
, 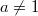 ,
, 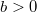 ,
, 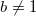 ,
, 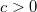 ,
, 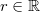 , то
, то
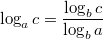 .
.
В частности,
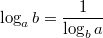 .
.
3. Показательная функция.
Функция 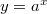 , где
, где 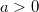 ,
, 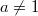 называется показательной.
называется показательной.
Ее область определения - это вся числовая ось, а множеством значений является множество положительных чисел.
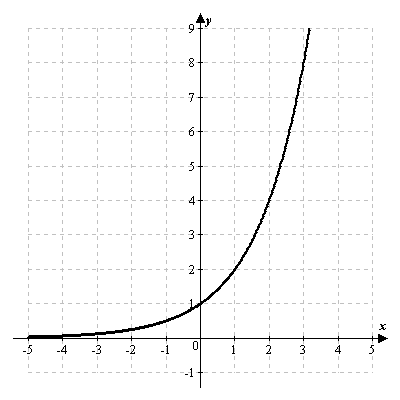
3.1. График показательной функции.
Если 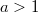 , то функция
, то функция 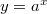 является строго возрастающей.
является строго возрастающей.
Если же 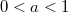 , то функция
, то функция 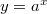 является строго убывающей.
является строго убывающей.
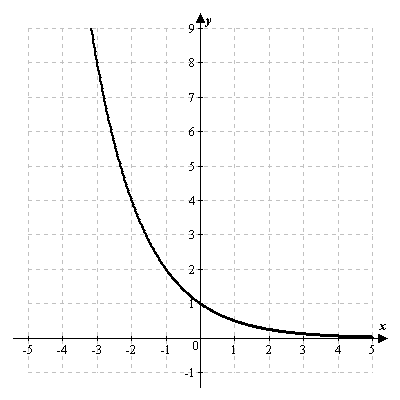
4. Логарифмическая функция.
Функция 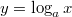 , где
, где 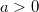 ,
, 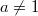 определена при
определена при 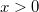 , множество ее значений - вся числовая ось.
, множество ее значений - вся числовая ось.
Показательная и логарифмическая функции являются взаимно обратными, то есть
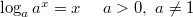 ,
,
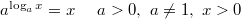 .
.
4.1. График логарифмической функции.
Если 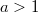 , то функция
, то функция 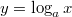 является строго возрастающей.
является строго возрастающей.
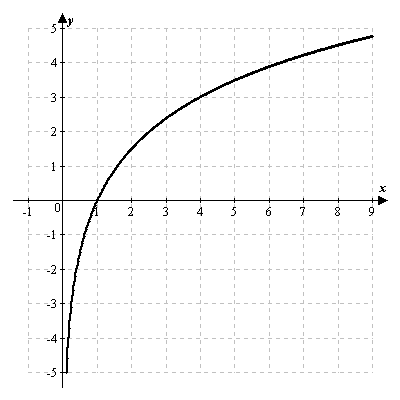
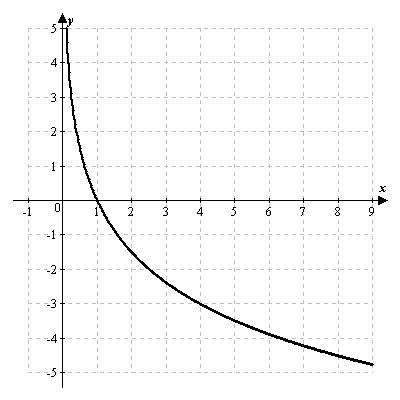
Если же 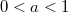 , то функция
, то функция 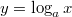 является строго убывающей.
является строго убывающей.
5. Простейшее показательные и логарифмическое уравнение.
Из монотонности показательной функции следует, что равенство 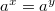 при
при 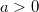 ,
, 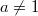 равносильно равенству
равносильно равенству 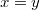 .
.
Уравнение 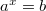 , где
, где 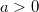 ,
, 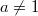 имеет единственное решение
имеет единственное решение 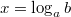 при любом действительном
при любом действительном 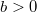 и не имеет решений при
и не имеет решений при 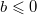 .
.
Уравнение 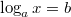 , где
, где 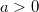 ,
, 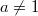 имеет единственное решение
имеет единственное решение 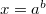 при любом действительном
при любом действительном  .
.
5.1. Потенцирование.
Уравнение 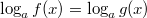 , где
, где 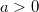 ,
, 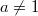 равносильно каждой из следующих систем.
равносильно каждой из следующих систем.
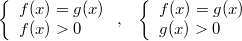
 2015-10-16
2015-10-16 18793
18793