Разновидности задач исследования операций и подходов к их решению

§ 4. Прямые и обратные задачи исследования операций. Детерминированные задачи

Задачи исследования операций делятся на две категории: а) прямые и б) обратные. Прямые задачи отвечают на вопрос: что будет, если в заданных условиях мы примем какое-то решение x є X? В частности, чему будет равен, при данном решении х, выбранный показатель эффективности W (или же ряд таких показателей)?

Для решения такой задачи строится математическая модель, позволяющая выразить один или несколько показателей эффективности через заданные условия и элементы решения.

Обратные задачи отвечают на вопрос: как выбрать решение х для того, чтобы показатель эффективности W обратился в максимум?

Естественно, прямые задачи проще обратных. Очевидно также, что для решения обратной задачи прежде всего надо уметь решать прямую. Для некоторых типов операций прямая задача решается настолько просто, что ею специально не занимаются. Для других типов операций построение математических моделей и вычисление показателя (показателей) эффективности само по себе далеко не тривиально (так, например, обстоит дело с прямыми задачами теории массового обслуживания, с которыми мы встретимся в главе 6).

Остановимся несколько подробнее на обратных задачах. Если число возможных вариантов решения, образующих множество X, невелико, то можно попросту вычислить величину W для каждого из них, сравнить между собой полученные значения и непосредственно указать один или несколько оптимальных вариантов, для которых W достигает максимума. Такой способ нахождения оптимального решения называется «простым перебором». Однако, когда число возможных вариантов решения, образующих множество X, велико, поиск среди них оптимального «вслепую», простым перебором, затруднителен, а зачастую практически невозможен. В этих случаях применяются методы «направленного перебора», обладающие той общей особенностью, что оптимальное решение находится рядом последовательных «попыток» или «приближений», из которых каждое последующее приближает нас к искомому оптимальному. С некоторыми из таких методов мы познакомимся в главах 3 и 4.

Сейчас мы ограничимся постановкой задачи оптимизации решения (обратной задачи исследования операций) в самой общей форме.

Пусть имеется некоторая операция О, на успех которой мы можем в какой-то мере влиять, выбирая тем или другим способом решение х (напомним, что х — не число, а целая группа параметров). Пусть эффективность операции характеризуется одним показателем W => max.

Возьмем самый простой, так называемый «детерминированный» случай, когда все условия операции полностью известны заранее, т. е. не содержат неопределенности. Тогда все факторы, от которых зависит успех операции, делятся на две группы:

1) заданные, заранее известные факторы (условия выполнения операции), которые мы для краткости обозначим одной буквой а;

2) зависящие от нас элементы решения, образующие в своей совокупности решение х.

Заметим, что первая группа факторов содержит, в частности, и ограничения, налагаемые на решение, т. е. определяет область возможных решений X.

Показатель эффективности W зависит от обеих групп факторов. Это мы запишем в виде формулы:

При рассмотрении формулы (4.1) не надо забывать, что как х, так и а в общем случае — не числа, а совокупности чисел (векторы), функции и т. д. В числе заданных условий а обычно присутствуют ограничения, налагаемые на элементы решения, имеющие вид равенств или неравенств.

Будем считать, что вид зависимости (4.1) нам известен, т. е. прямая задача решена. Тогда обратная задача формулируется следующим образом.

При заданном комплексе условий а найти такое решение х = х*, которое обращает показатель эффективности W в максимум.

Этот максимум мы обозначим:

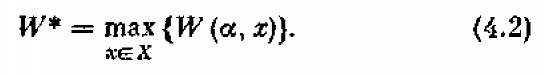
Формула (4.2) читается так: W* есть максимальное значение W(a, x), взятое по всем решениям, входящим в множество возможных решений X.

К формулам такого типа надо привыкать. Они понадобятся в дальнейшем (см. гл. 4).

Итак, перед нами — типичная математическая задача нахождения максимума функции или функционала

Эта задача принадлежит к классу так называемых «вариационных задач», хорошо разработанных в математике. Самые простые из таких задач («задачи на максимум и минимум») знакомы каждому инженеру. Чтобы найти максимум или минимум (короче, «экстремум») функции многих аргументов, надо продифференцировать ее по всем аргументам (в данном случае — элементам решения), приравнять производные нулю п решить полученную систему уравнений. Казалось бы, чего проще? А вот этот классический метод как раз в исследовании операций имеет весьма ограниченное применение. Во-первых, когда аргументов много, задача решения системы уравнений зачастую оказывается не проще, а сложнее, чем непосредственный поиск экстремума. Во-вторых, когда на элементы решения наложены ограничения, экстремум часто достигается не в точке, где производные равны нулю (такой точки может вообще не быть), а где-то на границе области X. Возникают все специфические трудности так называемой «многомерной вариационной задачи при ограничениях», иной раз непосильной по своей сложности даже для современных ЭВМ. Кроме того, в некоторых задачах функция W вообще не имеет производных (например, задана только для целочисленных значений аргументов). Все это делает задачу поиска экстремума далеко не такой простой, как она кажется с первого взгляда.

Метод поиска экстремума и связанного с ним оптимального решения х* должен всегда выбираться исходя из особенностей функции W и вида ограничений, накладываемых на решение. Например, если функция W линейно зависит от элементов решения x₁, x₂,..., а ограничения, налагаемые на x₁, x₂,..., имеют вид линейных равенств или неравенств, возникает ставшая классической задача линейного программирования, которая решается сравнительно простыми, а главное, стандартными методами (см. главу 3). Если функция W выпукла, применяются специальные методы выпуклого программирования с их разновидностью: «квадратичным программированием» (см. [8]). Для оптимизации управления многоэтапными операциями применяется метод динамического программирования (см. главу 4). Наконец, существует целый набор численных методов отыскания экстремумов, специально приспособленных для реализации на ЭВМ; некоторые из них включают элемент «случайного поиска», который для многомерных задач нередко оказывается эффективнее упорядоченного перебора.

Напомним, что «функционалом» называется величина, зависящая от вида функции. Если решение х включает не только числа, но и функции, величина W(a, х) является функционалом.

Таким образом, задача нахождения оптимального решения в простейшем, детерминированном случае есть чисто математическая задача, принадлежащая к классу вариационных (при отсутствии или наличии ограничений), которая может представить вычислительные, но не принципиальные трудности. Не так обстоит дело в случае, когда задача содержит элемент неопределенности.

§ 5. Проблема выбора решения в условиях неопределенности

В предыдущем параграфе мы рассмотрели обратную задачу исследования операций в детерминированном случае, когда показатель эффективности W зависит только от двух групп факторов: заданных, заранее известных а и элементов решения х. Реальные задачи исследования операций чаще всего содержат помимо этих двух групп еще одну — неизвестные факторы, которые в совокупности мы обозначим одной буквой ζ. Итак, показатель эффективности W зависит от всех трех групп факторов:

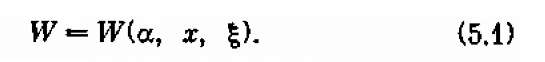
Так как величина W зависит от неизвестных факторов ζ, то даже при заданных α и х она уже не может быть вычислена, остается неопределенной. Задача поиска оптимального решения тоже теряет определенность. Ведь не можем же мы максимизировать неизвестную величину W! И все-таки нас не покидает желание сделать эту неизвестную величину по возможности максимальной. Ведь добиваются же успеха люди в условиях, когда не вся обстановка ясна? Иногда добиваются. Переводя сказанное на математический язык, поставим перед собой следующую задачу.

При заданных условиях а, с учетом неизвестных факторов ζ, найти такое решение xєX, которое, по возможности, обеспечивает максимальное значение показателя эффективности W.

Это уже другая, не чисто математическая задача (недаром в ее формулировке сделана оговорка «по возможности»). Наличие неопределенных факторов 4 переводит задачу в новое качество: она превращается в задачу о выборе решения в условиях неопределенности.

Порассуждаем немного о возникшей задаче. Прежде всего, будем честны: неопределенность есть неопределенность, и ничего хорошего в ней нет. Если условия операции неизвестны, мы не можем так же успешно оптимизировать решение, как мы это сделали бы, если бы располагали большей информацией. Поэтому любое решение, принятое в условиях неопределенности, хуже решения, принятого в заранее известных условиях. Что делать? Плохое или хорошее — решение все равно должно быть принято. Наше дело — придать этому решению в возможно большей мере черты разумности. Недаром Т. Л. Саати, один из видных зарубежных специалистов по исследованию операций, определяя свой предмет, говорит не без иронии: «Исследование операций представляет собой искусство давать плохие ответы на практические вопросы, на которые даются еще худшие ответы другими методами» [1].

Задача принятия решения в условиях неопределенности на каждом шагу встречается нам в жизни. Например, мы собрались путешествовать и укладываем в чемодан вещи. Размеры и вес чемодана, а также имеющийся у нас набор вещей заданы (условия а), погода в районе путешествия заранее неизвестна (условия 4). Какие предметы одежды (х) надо взять с собой? Эта задача, внешне сходная с задачами исследования операций, конечно, решается нами без всякой математики (незачем «стрелять из пушек по воробьям»), но все же не без опоры на некоторые статистические данные, скажем, о вероятной погоде в районе путешествия, а также собственной склонности к про­студам; нечто вроде оптимизации решения, сознательно или бессознательно, мы производим. Любопытно, что разные люди при этом, по-видимому, пользуются разными показателями эффективности. Если молодой человек, скорее всего, стремится максимизировать сумму приятных впечатлений (оставим в стороне вопрос о том, как ее оценить количественно), то пожилой путешественник, пожалуй, предпочтет минимизировать вероятность заболевания...

Теперь возьмем более серьезную задачу. Планируется ассортимент товаров для распродажи на ярмарке. Желательно было бы максимизировать прибыль. Однако заранее неизвестно ни количество покупателей, которые придут на ярмарку, ни потребности каждого из них. Как быть? Неопределенность налицо, а принимать решение нужно!

Другой пример: проектируется система сооружений, оберегающих район от паводков. Ни моменты их наступления, ни размеры заранее неизвестны. А проектировать все-таки нужно, и никакая неопределенность не избавит нас от этой обязанности...

Наконец, еще более сложная задача: разрабатывается план развития вооружения на несколько лет вперед. Неизвестны ни конкретный противник, ни вооружение, которым он будет располагать. А решение принимать надо!

Для того, чтобы такие решения принимать не наобум, по вдохновению, а трезво, с открытыми глазами, современная наука располагает рядом приемов. Каким из них воспользоваться — зависит от того, какова природа неизвестных факторов 4, откуда они возникают и кем контролируются. Другими словами, с какого вида неопределенностью мы в данной задаче сталкиваемся?

Возникает вопрос: неужели можно классифицировать неопределенности по «родам» и «сортам»? Оказывается, можно.

Прежде всего, рассмотрим наиболее благоприятный для исследования, так сказать, «доброкачественный» вид неопределенности. Это случай, когда неизвестные факторы 4 представляют собой обычные объекты изучения теории вероятностей - случайные величины (или случайные функции), статистические характеристики которых нам известны или в принципе могут быть получены к нужному сроку. Такие задачи исследования операций мы будем называть стохастическими задачами, а присущую им неопределенность — стохастической неопределенностью.

Приведем пример стохастической задачи исследования операций. Пусть организуется или реорганизуется работа столовой с целью повысить ее пропускную способность. Нам в точности неизвестно, какое количество посетителей придет в нее за рабочий день, когда именно они будут появляться, какие блюда заказывать и сколько времени будет продолжаться обслуживание каждого из них. Однако характеристики этих случайных величин, если сейчас еще не находятся в нашем распоряжении, могут быть получены статистическим путем.

Другой пример: организуется система профилактического и аварийного ремонта технических устройств с целью уменьшить простоя техники за счет неисправностей и ремонтов. Отказы техники, длительности ремонтов и профилактик носят случайный характер. Характеристики всех случайных факторов, входящих в задачу, могут быть получены, если собрать соответст­вующую статистику.

Рассмотрим более подробно этот «доброкачественный» вид неопределенности. Пусть неизвестные факторы | представляют собой случайные величины с какими- то, в принципе известными, вороятностными характеристиками — законами распределения, математическими ожиданиями, дисперсиями и т. п. Тогда показатель эффективности W, зависящий от этих факторов, тоже будет величиной случайной. Максимизи­ровать случайную величину невозможно: при любом решении х она остается случайной, неконтролируемой. Как же быть?

Первое, что приходит в голову: а нельзя ли заменить случайные факторы 4 их средними значениями (математическими ожиданиями)? Тогда задача становится детерминированной и может быть решена обычными методами.

Что и говорить — прием соблазнительный и в некоторых случаях даже оправданный. Ведь на практике, решая большинство задач физики, механики, техники, мы сплошь и рядом им пользуемся, пренебрегая случайностью ряда параметров (теплоемкость, индуктивность, коэффициент трения) и заменяя их средними значениями. Весь вопрос в том, насколько случайны эти параметры: если они мало отклоняются от своих математических ожиданий, так поступать можно и нужно. Так же обстоит дело и в исследовании операций: есть задачи, в которых случайностью можно пренебречь. Например, если мы составляем план снабжения группы предприятий сырьем (см. пример 1 § 1), можно в первом приближении пренебречь, скажем, случайностью фактической производительности источников сырья (если, разумеется, его производство хорошо налажено). Тот же прием — пренебречь случайностью и заменить все входящие в задачу случайные величины их математическими ожиданиями — будет уже опрометчивым, если влияние случайности на интересующий нас исход операции существенно. Возьмем самый грубый пример: пусть мы ведем обстрел какой-то цели, стремясь во что бы то ни стало попасть в нее. Произ­водится несколько выстрелов. Давайте заменим все случайные координаты точек попадания их математическим—ожиданием— центром цели. Получится, что любой выстрел с гарантией попадет в цель, что заведомо неверно. Другой, менее очевидный, пример: планируется работа ремонтной мастерской, обслуживающей автобазу. Пренебрежем случайностью момента появления неисправности (т. е. заменим случайное время безотказной работы машины его математическим ожиданием) и случайностью времени выполнения ремонта. И что же окажется? Мастерская, работа которой спла­нирована без учета случайности, попросту не будет справляться со своей задачей (в этом мы убедимся в главе 6). Встречаются (и очень часто) операции, в которые случайность входит по существу, и свести задачу к детерминированной не удается.

Итак, рассмотрим такую операцию О, где факторы 4 «существенно случайны» и заметно влияют на показатель эффективности W, который тоже «существенно случаен».

Возникает мысль: надо взять в качестве показателя эффективности среднее значение (математическое ожидание) этой случайной величины W = M[W] и выбрать такое решение х, при котором этот усредненный по условиям показатель обращается в максимум:

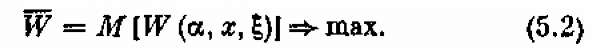
Заметим, что именно так мы поступали в § 2, выбирая в качестве показателя эффективности в задачах, содержащих неопределенность, не просто «доход», а «средний доход», не просто «время», а «среднее время». В большинстве случаев такой подход (мы его назовем «оптимизацией в среднем») вполне оправдан. В самом деле, если мы выберем решение так, чтобы среднее значение показателя эффективности обращалось в максимум, то, безусловно, поступим правильнее, чем если бы выбирали решение наобум.

А как же с элементом неопределенности? Конечно, в какой-то мере он сохраняется. Эффективность каждой отдельной операции, проводимой при конкретных значениях случайных факторов может сильно отличаться от ожидаемой как в большую, так, к сожалению, и в меньшую сторону. Нас может утешить то, что оптимизируя операцию «в среднем», мы в конечном счете после многих ее повторений выиграем больше, чем если бы совсем не пользовались расчетом.

Такая «оптимизация в среднем» очень часто применяется на практике в стохастических задачах исследования операций, и пользуются ею обычно не задумываясь над ее правомочностью. А задуматься надо! Чтобы этот прием был законным, нужно, чтобы операция обладала свойством повторяемости, и «недостача» показателя эффективности в одном случае компенсировалась его «избытком» в другом. Например, если мы предпринимаем длинный ряд однородных операций с целью получить максимальный доход, то доходы от отдельных операций суммируются, «минус» в одном случае покрывается «плюсом» в другом, и все в порядке.

Всегда ли это будет так? Нет, не всегда! Чтобы убедиться в этом, рассмотрим пример. Организуется автоматизированная система управления (АСУ) для службы неотложной медицинской помощи большого города. Вызовы, возникающие в разных районах города в случайные моменты, поступают на центральный пункт управления, откуда они передаются на тот или другой пункт неотложной помощи с приданными ему машинами. Требуется разработать такое правило (алгоритм) диспетчерской работы АСУ, при котором служба в целом будет функционировать наиболее эффективно. Для этого, прежде всего, надо выбрать показатель эффективности W.

Разумеется, желательно, чтобы время Т ожидания врача было минимально. Но это время — величина случайная. Если применить «оптимизацию в среднем», то надо выбрать тот алгоритм, при котором среднее время ожидания минимально. Не так ли?

Оказывается, не совсем так! Беда в том, что времена ожидания врача отдельными больными не суммируются: слишком долгое ожидание одного из них не компенсируется почти мгновенным обслуживанием другого. Выбирая в качестве показателя эффективности среднее время ожидания Т, мы рискуем дать предпочтение тому алгоритму, при котором среднее-то вре­мя ожидания мало, но отдельные больные могут ожидать врача очень долго! Чтобы избежать таких неприятностей, можно дополнить показатель эффективности добавочным требованием, чтобы фактическое время Т ожидания врача было не больше какого-то предельного значения t₀. Поскольку Т — величина слу­чайная, нельзя просто потребовать, чтобы выполнялось условие Т < t₀; можно только потребовать, чтобы оно выполнялось с очень большой вероятностью, настолько большой, чтобы событие Т < t₀ было прак­тически достоверным. Ну что же, назначим какое-то значение β, близкое к единице (например, 0,99 или 0,995), настолько близкое, что событие с такой вероятностью можно считать практически достоверным, и потребуем, чтобы условие Т < t₀ выполнялось с вероятностью, не меньшей, чем β:

Введение такого ограничения означает, что из области возможных решений X исключаются решения, ему не удовлетворяющие. Ограничения типа (5.3) называются стохастическими ограничениям и; наличие таких ограничений сильно усложняет задачу оптимизации.

Особенно осторожным надо быть с «оптимизацией в среднем», когда речь идет не о повторяемой, массовой операции, а о единичной, «уникальной». Все зависит от того, к каким последствиям может привести неудача данной операции, т. е. слишком малое значение показателя эффективности W; иногда оно может означать попросту катастрофу. Что толку в том, что операция в среднем приносит большой выигрыш, если в данном, единичном случае она может нас дотла разорить? От таких катастрофических результатов можно опять-таки спасаться введением стохастических ограничений. При достаточно большом значении уровня доверия в можно быть практически уверенным в том, что угрожающее разорение нас не постигнет^[1].

Итак, мы вкратце рассмотрели случай «доброкачественной» (стохастической) неопределенности и в общих чертах осветили вопрос об оптимизации решения в таких задачах. Но это, как говорится, цветочки, ягодки будут впереди! Стохастическая неопределенность — это почти определенность, если только известны вероятностные характеристики входящих в задачу случайных факторов. Гораздо хуже обстоит дело, когда неизвестные факторы 4 не могут быть изучены и описаны статистическими методами. Это бывает в двух случаях: либо а) распределение вероятностей для параметров 4 в принципе существует, но к моменту принятия решения не может быть получено, либо б) распределение вероятностей для параметров 4 вообще не существует.

Пример ситуации типа а): проектируется информационно-вычислительная система (ИВС), предназначенная для обслуживания каких-то случайных потоков требований (запросов). Вероятностные характеристики этих потоков требований в принципе могли бы быть получены из статистики, если бы данная ИВС (или аналогичная ей) уже существовала и функционировала достаточно долгое время. Но к моменту создания проекта такой информации нет, а решение принимать надо! Как быть?

Разумеется, можно заранее (из умозрительных соображений) задаться какими-то характеристиками случайных факторов 4, оптимизировать решение х на этой основе (просто «в среднем» или при стохастических ограничениях) и остановиться на нем. Это будет, безусловно, лучше, чем выбрать решение наобум, но не намного лучше. Гораздо разумнее будет применить следующий прием: оставить некоторые элементы решения х свободными, изменяемыми. Затем выбрать для начала какой-то вариант решения, зная заведомо, что он не самый лучший, и пустить систему в ход, а потом, по мере накопления опыта, целенаправленно изменять свободные параметры решения, добиваясь того, чтобы эффективность не уменьшалась, а увеличивалась. Такие совершенствующиеся в процессе применения алгоритмы управления называются адаптивными. Преимущество адаптивных алгоритмов в том, что они не только избавляют нас от предварительного сбора статистики, но и перестраиваются в ответ на изменение обстановки. По мере накопления опыта такой алгоритм постепенно улучшается, подобно тому, как живой человек «учится на ошибках».

Теперь обратимся к самому трудному и неприятному случаю б), когда у неопределенных факторов вообще не существует вероятностных характеристик; другими словами, когда их нельзя считать «случайными» в обычном смысле слова.

— Как? —Разве не всякая неопределенность есть случайность?

— Нет,— ответим мы,— лучше не путать эти понятия.

Поясняем: под термином «случайное явление» в теории вероятностей принято понимать явление, относящееся к классу повторяемых и, главное, обладающее свойством статистической устойчивости. При повторении однородных опытов, исход которых случаен, их средние характеристики проявляют тенденцию к устойчивости, стабилизируются. Частоты событий приближаются к их вероятностям, средние арифметические — к математическим ожиданиям. Если много раз бросать монету, частота появления герба постепенно стабилизируется, перестает быть случайной; если много раз взвешивать на аналитических весах одно и то же тело, средний результат перестает колебаться, выравнивается. Это пример доброкачественной, стохастической неопределенности.

Однако бывает неопределенность и нестохастического вида, которую мы условно назовем «дурной неопределенностью». Несмотря на то, что факторы ζ заранее неизвестны, не имеет смысла говорить об их «законах распределения» или других вероятностных характеристиках.

Пример: допустим, планируется некая торгово-промышленная операция, успех которой зависит от того, юбки какой длины ζ будут носить женщины через два года. Распределение вероятностей для величины ζ в принципе не может быть получено ни из каких статистических данных. Даже если рассмотреть великое множество опытов (годов), начиная с тех отдаленных времен, когда женщины впервые надели юбки, и в каждом из них зарегистрировать величину ζ, это вряд ли поможет нам в нашем прогнозе. Вероятностное распределение величины ζ попросту не существует, так как не существует массива однородных опытов, где она обладала бы должной устойчивостью. Налицо случай «дурной неопределенности».

Как же все-таки быть в таких случаях? Отказаться вообще от применения математических методов и выбрать решение «волевым» образом? Нет, этого делать не стоит. Некоторую пользу предварительные расчеты могут принести даже в таких скверных условиях.

Давайте поразмышляем на эту тему. Пусть выбирается решение х в какой-то операции О, условия которой содержат «дурную неопределенность» — параметры ζ, относительно которых никаких сведений мы не имеем, а можем делать лишь предположения. Попробуем все же решить задачу.

Первое, что приходит в голову: а ну-ка, зададимся какими-то, более или менее правдоподобными, значениями параметров ζ. Тогда задача перейдет в категорию детерминированных и может быть решена обычными методами (детерминированный случай, со всеми его трудностями, представляется нам теперь чуть ли не «курортом»!).

Нет, радоваться рано. Допустим, что, затратив много усилий и времени (своего и машинного), мы это сделали. Ну и что? Будет ли найденное решение хорошим для других условий ζ? Как правило, нет. Поэтому ценность его — сугубо ограниченная. В данном случае разумно будет выбрать не решение х, оптимальное для каких-то условий ζ, а некое компромиссное решение, которое, не будучи оптимальным, может быть, ни для каких условий, будет все же приемлемым в целом их диапазоне.

В настоящее время полноценной научной теории компромисса не существует, хотя некоторые попытки в этом направлении в теории игр и статистических решений делаются (см. главу 8). Обычно окончательный выбор компромиссного решения осуществляется человеком. Опираясь на предварительные расчеты, в ходе которых решается большое число прямых задач исследования операций для разных условий ζ и разных вариантов решения х, он может оценить сильные и слабые стороны каждого варианта и на этой основе сделать выбор. Для этого необязательно (хотя иногда и любопытно) знать точный «условный» оптимум для каждой совокупности условий ζ. Математические вариационные методы в данном случае отступают на задний план.

Подчеркнем еще одну полезную функцию предварительных математических расчетов в задачах с «дурной неопределенностью»: они помогают заранее отбросить те решения xєX, которые при любых условиях ζ уступают другим, т. е. оказываются неконкурентоспособными. В ряде случаев это помогает существенно сузить множество X, иногда свести его к небольшому числу вариантов, которые легко могут быть просмотрены и оценены человеком в поисках удачного компромисса.

При рассмотрении задач исследования операций с «дурной неопределенностью» всегда полезно сталкивать в споре разные подходы, разные точки зрения. Среди последних надо отметить одну, часто применяемую в силу своей математической определенности, которую можно назвать «позицией крайнего пессимизма». Она сводится к тому, что, принимая решение в условиях «дурной неопределенности», надо всегда рассчитывать на худшее и принимать то решение, которое дает максимальный эффект в наихудших условиях.., Если в этих условиях мы получаем выигрыш W = Ẃ, то можно гарантировать, что в любых других он будет не меньше («принцип гарантированного результата»). Этот подход привлекателен тем, что дает четкую постановку задачи оптимизации и возможность ее решения корректными математическими методами. Но он оправдан далеко не всегда. Область его применения — по преимуществу так называемые «конфликтные ситуации», в которых условия зависят от сознательно действующего лица («разумного противника»), отвечающего на любое наше решение наихудшим для нас образом. В более нейтральных ситуациях принцип «гарантированного выигрыша» не является единственно возможным, но может быть рассмотрен наряду с другими. Пользуясь им, нельзя забывать, что эта точка зрения — крайняя, что на ее основе можно выбрать только очень осторожное, «перестраховочное» решение, которое не всегда будет разумным. Вообразите себе, например, военачальника, который всякое свое решение будет принимать исходя из гипотезы, что его противник необычайно умен, хитер и изворотлив и на каждое его действие немедленно ответит наихудшим для него образом. Вряд ли такому военачальнику будет сопутствовать удача! Напротив, в любой конкретной ситуации нужно стараться угадать, в чем слаб и «глуп» противник, и стараться «обвести его вокруг пальца». Тем менее уместен крайне пессимистический подход в ситуациях, где стороне, принимающей решение, не противостоят никакие враждебные силы. Расчеты, основанные на точке зрения «крайнего пессимизма», всегда должны корректироваться разумной долей оптимизма. Вряд ли стоит становиться и на противоположную точку зрения — крайнего или «залихватского» оптимизма, но известная доля риска при принятии решения все же должна присутствовать. Нельзя также забывать о том, что любое решение, принятое в условиях «дурной неопределенности»,— неизбежно плохое решение, и вряд ли стоит обосновывать его с помощью тонких и кропотливых расчетов. Скорее следует подумать о том, откуда можно было бы взять недостающую информацию. Здесь все способы хороши — лишь бы прояснить положение.

Упомянем в этой связи об одном довольно оригинальном методе, не пользующемся любовью в среде чистых математиков, но тем не менее полезном, а иногда — единственно возможном. Речь идет о так называемом методе экспертных оценок. Он часто применяется в задачах, связанных с прогнозированием в условиях дурной неопределенности (на­пример, в футурологии). Грубо говоря, идея метода сводится к следующему: собирается коллектив сведущих, компетентных в данной области людей, и каждому из них предлагается ответить на какой-то вопрос (например, назвать срок, когда будет совершено то или другое открытие, или оценить вероятность того или другого события). Затем полученные ответы обрабатываются наподобие статистического материала. Результаты обработки, разумеется, сохраняют субъективный характер, но в гораздо меньшей степени, чем если бы мнение высказывал один эксперт («ум хорошо, а два — лучше»). Подобного рода экспертные оценки для неизвестных условий могут быть применены и при решении задач исследования операций с дурной неопределенностью. Каждый из экспертов на глаз оценивает степень правдоподобия различных вариантов условий 4, приписывая им какие-то субъективные вероятности. Несмотря на субъективный характер оценок каждого эксперта, усредняя оценки целого коллектива, можно получить нечто более объективное и полезное (кстати, оценки разных экспертов расходятся не так сильно, как можно было бы ожидать). Таким образом, задача с дурной неопределенностью как бы сводится к обычной стохастической задаче. Разумеется, к полученным отсюда выводам не надо относиться слишком доверчиво, но наряду с другими результатами, вытекающими из других точек зрения, они все же могут помочь при выборе решения.

Наконец, сделаем одно общее замечание. При обосновании решения в условиях неопределенности, что бы мы ни делали, элемент неопределенности, «гада- тельности» сохраняется. Поэтому нельзя предъявлять к точности решений слишком высокие требования. Вместо того, чтобы указать одно-единственное, в точности «оптимальное» (с какой-то точки зрения) решение, лучше выделить целую область «приемлемых» решений, которые оказываются несущественно хуже других, какой бы точкой зрения мы ни пользовались. В пределах этой области и должны производить свой окончательный выбор ответственные за это люди. Исследователь, предлагая им рекомендации по выбору решения, всегда должен одновременно указывать точки зрения, из которых вытекают те или другие рекомендации.

§ 6. Многокритериальные задачи исследования операций. «Системный подход»

Несмотря на ряд существенных трудностей, связанных с неопределенностью, мы до сих пор рассматривали только самые простые случаи, когда ясен критерий, по которому производится оценка эффективно­сти, и требуется обратить в максимум (минимум) один - единственный показатель W. К сожалению, на практике такие задачи, где критерий оценки однозначно диктуется целевой направленностью операции, встречаются не так уж часто — преимущественно при рассмотрении небольших по масштабу и скромных по значению мероприятий. А когда идет речь о круп­номасштабных, сложных операциях, затрагивающих разнообразные интересы их организаторов и общества в целом, то их эффективность, как правило, не может быть полностью охарактеризована с помощью одного - единственного показателя эффективности W. На помощь ему приходится привлекать другие, дополнительные. Такие задачи исследования операций называются многокритериальными.

Рассмотрим пример такой задачи. Организуется оборона важного объекта от воздушных налетов. В нашем распоряжении — какие-то средства противовоздушной обороны, которые надо разумным образом разместить вокруг объекта, организовать их взаимодействие, распределить между ними цели, назначить боезапас и т. д. Допустим, что каждый из самолетов противника, участвующих в налете, является потенциальным носителем мощного поражающего средства, которое, будучи применено по объекту, гарантирует его уничтожение. Тогда главная задача операции — не допустить к объекту ни одного самолета, а естественный показатель эффективности — вероятность W того, что ни один самолет не прорвется к объекту. Но единст­венный ли это важный для нас показатель? Безусловно, нет. При одной и той же вероятности W мы предпочтем все-таки решение, при котором будет погибать в среднем побольше самолетов противника. Отсюда второй показатель эффективности М — среднее число пораженных целей, который нам тоже хотелось бы максимизировать. Кроме того, нам далеко не все равно, каковы будут наши собственные боевые потери П — еще один критерий, который хотелось бы минимизировать. Желательно было бы, кроме того, сделать поменьше средний расход боеприпасов R, и т. д.

Другой пример — на этот раз из совершенно мирной области. Организуется (или реорганизуется) работа промышленного предприятия. Под углом зрения какого критерия надо выбирать решение? С одной стороны, нам хотелось бы обратить в максимум валовый объем продукции V. Желательно также было бы получить максимальный чистый доход D. Что касается се­бестоимости S, то ее хотелось бы обратить в минимум, а производительность труда П — в максимум. При обдумывании задачи может возникнуть еще ряд допол­нительных критериев.

Такая множественность показателей эффективности, из которых одни желательно обратить в максимум а другие — в минимум, характерна для любой сколько- нибудь сложной задачи исследования операций. Предлагаем в виде упражнения попытаться сформулировать ряд критериев, по которым будет оцениваться работа автобусного парка. Подумайте о том, какой из них, с вашей точки зрения, является главным (теснее всего связанным с целевой направленностью операции), а остальные (дополнительные) расположите в порядке убывающей важности. На этом примере можно убедиться в том, что а) ни один из показателей не может быть выбран в качестве единственного и б) формулировка системы показателей — не такая уж простая задача... И сами показатели и их упорядоченность по важности зависят от того, с точки зрения чьих интересов оптимизируется решение.

Итак, типичной для крупномасштабной задачи исследования операций является многокритериальность — наличие ряда количественных показателей W₁, W₂,..., одни из которых желательно обратить в максимум, другие — в минимум («чтобы и волки были сыты, и овцы целы»).

Спрашивается, можно ли найти решение, одновременно удовлетворяющее всем этим требованиям? Со всей откровенностью ответим: нет. Решение, обращающее в максимум один какой-то показатель, как правило, не обращает ни в максимум, ни в минимум другие. Поэтому часто применяемая формулировка: «достигнуть максимального эффекта при минимальных затратах» представляет собой не более чем фразу и при научном анализе должна быть отброшена.

Как же быть в случае, если все же приходится оценивать эффективность операции по нескольким показателям?

Люди, малоискушенные в исследовании операций, обычно торопятся свести многокритериальную задачу к однокритериальной: составляют какую-то функцию от всех показателей и рассматривают ее как один, «обоб­щенный» показатель, по которому и оптимизируется решение. Часто такой обобщенный показатель имеет вид дроби, в числителе которой стоят все величины, увеличение которых желательно, а в знаменателе — те, увеличение которых нежелательно. Например, продуктивность и доход — в числителе, время выполнения и расходы — в знаменателе и т. д.

Такой способ объединения нескольких показателей в один не может быть рекомендован, и вот почему: он основан на неявном допущении, что недостаток в одном показателе всегда может быть скомпенсирован за счет другого; например, малая продуктивность — за счет низкой стоимости и т. д. Это, как правило, несправедливо.

Вспомним «критерий для оценки человека», полушутя-полусерьезно предложенный когда-то Львом Толстым. Он имеет вид дроби, в числителе которой стоят действительные достоинства человека, а в знаменателе — его мнение о себе. С первого взгляда такой подход может показаться логичным. Но представим себе человека, почти совсем не имеющего достоинств, но совсем не обладающего самомнением. По критерию Л. Н. Толстого такой человек должен иметь бесконечно большую ценность, с чем уж никак согласиться нельзя...

К подобным парадоксальным выводам может привести (и нередко приводит) пользование показателем в виде дроби, где, как говорят, все, что «за здравие»,— в числителе, все, что «за упокой»,—в знаменателе.

Нередко применяется и другой, чуть более замысловатый, способ составления «обобщенного показателя эффективности»—он представляет собой «взвешенную сумму» частных показателей, в которую каждый из них Wi входит с каким-то «весом» а _і отражающим его важность:

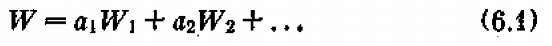
(для тех показателей, которые желательно увеличить, веса берутся положительными, уменьшить — отрицательными).

При произвольном назначении весов а _і, а ₂,... этот способ ничем не лучше предыдущего (разве тем, что обобщенный критерий не обращается в бесконечность). Его сторонники ссылаются на то, что и человек, принимая компромиссное решение, тоже мысленно взвешивает все «за» и «против», приписывая больший вес более важным для него факторам. Это, может быть, и так, но, по-видимому, «весовые коэффициенты», с которыми входят в расчет разные показатели, не постоянны, а меняются в зависимости от ситуации.

Поясним это элементарным примером. Человек выходит из дому, чтобы ехать на работу, боится опоздать и размышляет: каким транспортом воспользоваться? Трамвай ходит часто, но идет долго; автобус — быстрее, но с большими интервалами. Можно, конечно, взять такси, но это обойдется дорого. Есть еще такое решение: часть пути проехать на метро, а затем взять такси. Но на стоянке может не быть машин, а добираясь до работы со станции метро пешком, он рискует опоздать больше, чем если бы ехал автобусом. Как ему поступить?

Перед нами типичная (намеренно упрощенная) за­дача исследования операций с двумя критериями (по­казателями). Первый — среднее ожидаемое время опоздания Т, которое хотелось бы сделать минимальным. Второй — ожидаемая стоимость проезда S; ее тоже желательно сделать минимальной. Но эти два требования, как мы знаем, несовместимы, поэтому человек должен принять компромиссное, приемлемое по обоим критериям, решение. Возможно, он при этом подсознательно взвешивает все «за» и «против», пользуясь чем-то вроде обобщенного показателя:

W = a₁T + a₂S =>min. (6.2)

Но беда в том, что весовые коэффициенты а_і, а₂ никак нельзя считать постоянными. Они зависят как от самих величин Т и S, так и от обстановки. Например, если человек недавно уже получил выговор за опоздание, коэффициент при Т у него, вероятно, увеличится, а на другой день после получки, вероятно, уменьшится коэффициент при S. Если же назначать (как это обычно и делается) веса а_і, а₂ произвольно, то, по существу, столь же произвольным будет и вытекающее из них «оптимальное» решение.

Здесь мы встречаемся с очень типичным для подобных ситуаций приемом — «переносом произвола из одной инстанции в другую». Простой выбор компромиссного решения на основе мысленного сопоставления всех «за» и «против» каждого решения кажется слишком произвольным, недостаточно «научным». А вот маневрирование с формулой, включающей (пусть столь же произвольно назначенные) коэффициенты а_і, а₂,...,— совсем другое дело. Это уже «наука»! По существу же никакой науки тут нет, и нечего обманывать самих себя.

«Гони природу в дверь — она влетит в окно». Нечего надеяться полностью избавиться от субъективности в задачах, связанных с выбором решений. Даже в простейших, однокритериальных задачах она неизбежно присутствует, проявляясь хотя бы в выборе показателя эффективности и математической модели явления. Тем более неизбежна субъективность (грубо говоря, произвол) при выборе решения в многокритериальной задаче. Правда, бывают редкие случаи, когда достаточно ознакомиться со значениями всех показателей для каждого варианта, чтобы сразу стало ясно, какой из них выбрать. Представим себе, например, что какой-то вариант решения х имеет преимущество над другими по всем показателям; ясно, что именно его следует предпочесть. Но гораздо чаще встречаются случаи, когда с первого взгляда ситуация неясна: один из показателей тянет в одну сторону, другой — в другую. При этом всегда полезно провести дополнительные расчеты, пользуясь, может быть, даже формулами типа (6.1), но не доверяя им слепо, а сохраняя к ним критическое отношение.

Выходит, что математический аппарат не может нам ничем помочь при решении многокритериальных задач? Отнюдь нет, он может помочь, и очень существенно. Прежде всего он позволяет решать прямые задачи исследования операций, т. е. для любого решения х находить значения показателей эффективности W_j, W₂,..., сколько бы их ни было (кстати, для прямых задач многокритериальность — не помеха). И во-вторых, что особенно важно, он помогает «выбраковать» из множества возможных решений X заведомо неудачные, уступающие другим по всем критериям.

Покажем, как это, в принципе, делается. Пусть имеется многокритериальная задача исследования операций с к критериями W_j,, W₂,..., W_k. Для простоты предположим, что все эти величины желательно мак­симизировать (как переходить от «минимума» к «максимуму», мы уже знаем). Пусть в составе множества возможных решений есть два решения х₁ и х₂ такие, что все критерии W_j,, W₂,..., W_k для первого решения больше или равны соответствующим критериям для второго решения, причем хотя бы один из них действительно больше. Очевидно, тогда в составе множества X нет смысла сохранять решение х ₂, оно вытесняется (или, как говорят, «доминируется») решением х₁. Ладно, выбросим решение х ₂ как неконкурентоспособное и перейдем к сравнению других по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество X обычно сильно уменьшается: в нем сохраняются только так называемые эффективные (иначе «паретовские») решения, характерные тем, что ни для одного из них не существует доминирующего решения.

Проиллюстрируем прием выделения паретовских решений на примере задачи с двумя критериями: W_j и W₂ (оба требуется максимизировать). Множество X состоит из конечного числа п возможных решений х₁, х₂,..., х_п. Каждому решению соответствуют определенные значения показателей W_j,, W₂; будем изображать решение точкой на плоскости с координатами W_j,, W₂ и занумеруем точки соответственно номеру решения (рис. 6.1),

Очевидно, из всего множества X эффективными будут только решения х₂, х₅, х₁₀, х₁₁, лежащие на правой верхней границе области возможных решений (см. жирные точки, соединенные пунктиром, на рис. 6.1). Для всякого другого решения существует хотя бы одно доминирующее, для которого либо W_j, либо W₂, либо оба больще, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих не существует.

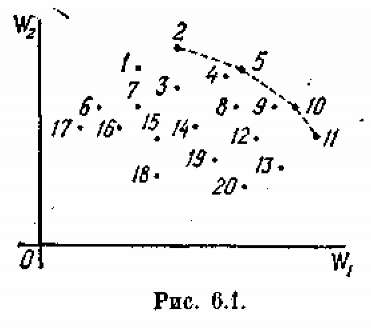Когда из множества возможных решений выделены эффективные, «пере говоры» могут вестись уже в пределах этого «эффективного» множества. На рис. 6.1 его образуют четыре решения: х₂, х₅, х₁₀ и х_и из них х_и — наилучшее по критерию W₁, х₂ — по критерию W₂. Дело лица, принимающего решение, выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям.

Аналогично строится множество эффективных решений и в случае, когда показателей не два, а больше (при числе их, большем трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется). Множество эффективных решений легче обозримо, чем множество X. Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. Только человек, с его непревзойденным умением решать неформальные задачи, принимать так называемые «компромиссные решения» (не строго- оптимальные, но приемлемые по ряду критериев) может взять на себя ответственность за окончательный выбор.

Однако сама процедура выбора решения, будучи повторена неоднократно, может послужить основой для выработки некоторых формальных правил, применяемых уже без участия человека. Речь идет о так называемых «эвристических» методах выбора решений. Предположим, что опытный человек (или, еще лучше, группа опытных людей) многократно выбирает компромиссное решение в многокритериальной задаче исследования операций, решаемой при разных условиях а. Набирая статистику по результатам выбора, можно, например, разумным образом подобрать значения «весов» а_ь а₂,... в формуле (6.1), в общем случае зависящие от условий а и самих показателей W₁,, W₂,..., и воспользоваться таким обобщенным критерием для выбора решения, на этот раз уже автоматического, без участия человека. На это иногда приходится идти в случаях, когда времени на обдумывание компромиссного решения нет (например, в условиях боевых действий), или же в случае, когда выбор решения передается автоматизированной системе управления (АСУ).

В некоторых случаях очень полезной оказывается процедура выбора решения в так называемом «диалоговом режиме», когда машина, произведя расчеты, выдает лицу (лицам), управляющему операцией, значения показателей W_b, W₂,..., а это лицо, критически оценив ситуацию, вносит изменения в весовые коэффициенты (или иные параметры управляющего алгоритма).

Существует один, часто применяемый способ свести многокритериальную задачу к однокритериальной — это выделить один (главный) показатель W₁ и стремиться его обратить в максимум, а на все остальные W₂,, W₃,... наложить только некоторые ограничения, потребовав, чтобы они были не меньше каких-то заданных w₂, w₃,... Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту — выполнен или перевыполнен, а себестоимость продукции — не выше заданной. При таком подходе все показатели, кроме одного — главного, переводятся в разряд заданных условий а. Известный произвол в назначении границ w₂, w₃,..., разумеется, при этом остается; поправки в эти границы тоже могут быть введены в «диалоговом режиме».

Существует еще один путь построения компромиссного решения, который можно назвать «методом последовательных уступок». Предположим, что показатели W_j,, W₂,... расположены в порядке убывающей важности. Сначала ищется решение, обращающее в максимум первый (важнейший) показатель Wj= W_j*. Затем назначается, исходя из практических соображений, с учетом малой точности, с которой нам известны входные данные, некоторая «уступка» AW₁, которую мы согласны сделать для того, чтобы максимизировать второй показатель W₂. Наложим на показатель W₁ ограничение: потребуем, чтобы он был не меньше, чем W₁*—AW₁, и при этом ограничении ищем решение, обращающее в максимум W₂. Далее снова назначим «уступку» в W₂, ценой которой можно максимизировать W₃, и т. д. Такой способ построения компромиссного решения хорош тем, что здесь сразу видно, ценой какой «уступки» в одном показателе приобретается выигрыш в другом и какова величина этого выигрыша.

Так или иначе, при любом способе ее постановки, задача обоснования решения по нескольким показателям остается не до конца формализованной, и окончательный выбор решения всегда определяется волевым актом «командира» (так можно условно назвать ответственное за выбор лицо). Дело исследователя — предоставить в распоряжение командира данные, помогающие ему делать выбор не «вслепую», а с учетом преимуществ и недостатков каждого варианта решения.

В заключение скажем несколько слов о так называемом «системном подходе» к задачам выбора решений.

В настоящее время в связи с ростом масштабов и сложности операций все чаще приходится решать задачи оптимального управления так называемыми «сложными системами», включающими большое число элементов и подсистем и организованными обычно по иерархическому принципу. Например, какая-то отрасль народного хозяйства включает относительно самостоятельные специализированные управления, которые, в свою очередь, имеют в своем подчинении предприятия (фабрики, заводы); каждое предприятие включает подразделения, цеха и проч. Оптимизируя (с точки зрения какого-либо критерия) работу одного звена сложной системы, нельзя забывать о связях, имеющихся между разными звеньями системы, между разными уровнями иерархии. Нельзя вырывать из цепи одно звено и рассматривать его, забывая об остальных.

Простейший пример: пусть, оптимизируя работу заводского цеха, мы добились резкого увеличения объема продукции — это хорошо. Но готовые изделия скапливаются (в лучшем случае — на складах, а в худшем — во дворе), а транспортные средства не готовы к вывозу всей этой продукции. Такая ситуация может привести к материальным потерям, сводящим на нет выигрыш за счет увеличения продукции.

Другой пример: стремясь к перевыполнению плана по «валу», фабрика в огромном количестве выпускает изделия, не пользующиеся спросом, быстро переходящие в разряд «уцененных», что, разумеется, тоже ведет к потерям. Все это — результат «несистемного», «локального» планирования.

Какой из этого выход? Разумеется, не в жестком планировании работы всей огромной системы, когда в верхнем звене управления планируется все без исключения, вплоть до гвоздя, забитого в доску в каждом цехе. Это не только невозможно — к этому не надо и стремиться. Разумное управление сложной иерархической системой состоит в том, чтобы каждое вышестоящее звено давало задания нижестоящим не жестко регламентированно, а «в общих чертах», предоставляя им известную инициативу, но так ставя перед ними цели, чтобы каждое звено, стремясь к своей цели, работало вместе с тем в согласии с интересами вышестоящего звена и системы в целом.

Это, разумеется, легче сказать, чем сделать. Математическая теория больших иерархических систем в настоящее время еще только разрабатывается. Создается математический аппарат, пригодный для описания таких систем, разрабатываются приемы «декомпозиции» больших систем на более удобные в рассмотрении «небольшие» элементы, но действенных методов управления такими системами пока не создано. На практике «системный подход» в исследовании операций сводится пока что к тому, что каждое звено, работа которого оптимизируется, полезно рассмотреть как часть другой, более обширной системы, и выяснить, как влияет работа данного звена на работу последней.